| Базовый вектор | Включенные ключи | Схема включения ключей | Фазные напряжения | ||

| 
| 
| |||
 (фаза А)
(фаза А)
| V 1, V 2, V 6 | 
| 
| 
| |
 (фаза B)
(фаза B)
| V 2, V 1, V 3 | 
| 
| 
| |
 (фаза C)
(фаза C)
| V 3, V 2, V 4 | 
| 
| 
| |
 (фаза А)
(фаза А)
| V 3, V 2, V 4 | 
| 
| 
| |
 (фаза C)
(фаза C)
| V 5, V 4, V 6 | 
| 
| 
| |
 (фаза B)
(фаза B)
| V 6, V 1, V 5 | 
| 
| 
| |

| V 2, V 4, V 6 |
Уравнение (2.11) определяют среднее значение пространственного вектора напряжения  как линейную комбинацию составляющих векторов, выполнение равенства (2.12) означает, что сумма промежутков времени должна равняться периоду ШИМ. В дополнение приведенным уравнениям вводятся ограничения, указывающие на то, что относительные продолжительности включения не могут быть отрицательными:
как линейную комбинацию составляющих векторов, выполнение равенства (2.12) означает, что сумма промежутков времени должна равняться периоду ШИМ. В дополнение приведенным уравнениям вводятся ограничения, указывающие на то, что относительные продолжительности включения не могут быть отрицательными:
0≤ γ 1≤1; 0≤ γ 2≤1; 0≤γ0≤1. (2.14)
Запишем вектор среднего напряжения  и базовые векторы
и базовые векторы  , через их проекции на оси неподвижной системы координат:
, через их проекции на оси неподвижной системы координат:
 . (2.15)
. (2.15)
Т а б л и ц а 2.3 Результаты расчета Um / Ud
| Величина | Значение величины | ||||||
| θ | 60 º | 70 º | 80 º | 90 º | 100 º | 110 º | 120 º |
| Um / Ud | 0,667 | 0,614 | 0,586 | 0,577 | 0,586 | 0,614 | 0,667 |
На основании выражения (2.11) и равенстве нулю проекции нулевых векторов  , можно записать проекции вектора требуемого напряжения через проекции базовых векторов:
, можно записать проекции вектора требуемого напряжения через проекции базовых векторов:
 . (2.16)
. (2.16)
При записи через косинусы углов, обозначенных на рис. 2.11, последние равенства приобретут вид:
 ; (2.17).
; (2.17).
 . (2.18)
. (2.18)
Здесь U m – модуль требуемого пространственного вектора напряжения; U – модуль базового вектора  .
.
Решая совместно уравнения (2.17), (2.18) найдем относительные продолжительности включения состояния ключей инвертора, необходимых для получения вектора U, расположенного во втором секторе:
 . (2.19)
. (2.19)
На основании равенства (2.12) можно определить требуемую относительную продолжительность включения нулевого вектора
γ 0 = 1-- (γ 1 – γ 2). (2.20)
Уравнения (2.19) можно переписать для любого n –сектора:
 ;. (2.21)
;. (2.21)
При подстановке в выражения (2.21) и получим: n = 2 и U =2/3 U d
 . (2.22)
. (2.22)
Для максимально возможного значения модуля пространственного вектора нулевые вектора не используется, т.е. γ 0 = 0 и, следовательно, γ 1+ γ 2=1, тогда с учетом выражений (2.22) запишем
 . (2.23)
. (2.23)
Уравнение (2.23) может быть использовано для определения максимального значения U m/ U d в зависимости от угла поворота заданного пространственного вектора относительно оси α. Результаты расчета сведены в табл. 2.3. Из них легко убедиться, что годографом концов вектора  в пределах сектора является прямая линия abc (см. рис. 2.11).
в пределах сектора является прямая линия abc (см. рис. 2.11).
Чтобы форма напряжения на выходе инвертора в максимальной степени приближалась к синусоиде, годограф концов заданного вектора должен представлять собой окружность (см. рис. 2.11). Для этого следует за максимальную длину вектора напряжения выбрать значение
Um .max = Ud / √3 ≈ 0.577 Ud, тогда выражения (2.22) примут вид:
 ; (2.24)
; (2.24)
 , (2.25)
, (2.25)
где  – коэффициент модуляции.
– коэффициент модуляции.
Если μ =1, то при всех значениях угла поворота θ, кроме θ = 30°, 90°, 150°, 210°, 270°, 330°, в формировании заданного пространственного вектора  должен участвовать один из нулевых векторов
должен участвовать один из нулевых векторов  .
.
Относительная продолжительность его включения определяется по формуле (2.20) при значениях γ1 и γ2, рассчитанных по выражениям (2.24), (2.25). Результаты расчета для вектора расположенного в секторе 2, приведены в табл. 2.4.
Т а б л и ц а 2.4.
Результаты расчета γ 1, γ 2, γ 0
| Величина | Значение величины | ||||||
| θ | 60 º | 70 º | 80 º | 90 º | 100 º | 110 º | 120 º |
| γ1 | 0,866 | 0,765 | 0,645 | 0,5 | 0,342 | 0,173 | |
| γ2 | 0,173 | 0,342 | 0,5 | 0,642 | 0,765 | 0,866 | |
| γ0 | 0,134 | 0,062 | 0,016 | 0,016 | 0,062 | 0,134 |
Уравнения (2.24), (2.25) справедливы для пространственного вектора  , расположенного в любом из шести возможных секторах:
, расположенного в любом из шести возможных секторах:
γ1 = μ ∙sin(n ∙60°-θ); γ2 = μ ∙sin(θ- (n -1 ) ∙60°), (2.26)
где n = 1, 2 … 6 – номер сектора, в котором находится заданный пространственный вектор.
Максимально возможная амплитуда фазного напряжения при модуляции по синусоидальному закону и векторной ШИМ
Uфm .max = U m.max = U d /√3. (2.27)
Тогда максимальное действующее значение фазного напряжения
Uф .max = U d /√6. (2.28)
Действующее значение линейного напряжения в √3 раз больше
Uл .max = U d /√2. (2.29)
При частотном регулировании на выходе АИН по соответствующему закону необходимо регулировать амплитуду и частоту трехфазного выходного напряжения. Регулирование амплитуды достигается за счет изменения коэффициента модуляции m в формулах (2.26), (2.20). При этом уменьшение m приводит к снижению относительных продолжительностей включения ненулевых векторов γ 1 и γ 2 и увеличению относительной продолжительности включения нулевого вектора γ 0 и, следовательно, к уменьшению среднего значения напряжения за период ШИМ.
Регулирование частоты на выходе АИН достигается за счет изменения скорости вращения (угла поворота) пространственного вектора в полярной системе координат. Вращение пространственного вектора  в обратном направлении приводит к изменению чередования фаз на выходе АИН и, следовательно, изменению направления вращения двигателя. Сначала определяется номер сектора n, в котором находится заданный пространственный вектор. Затем на каждом периоде ШИМ рассчитываются значения γ 1 и γ 2 по формулам (2.26). По ним определяются уровни переключения УП 1= γ 1 и УП 2= γ 1 + γ 2 , при сравнении которых с пилообразным сигналом осуществляется переключение базовых векторов. Алгоритм переключений представляет собой следующую последовательность действий:
в обратном направлении приводит к изменению чередования фаз на выходе АИН и, следовательно, изменению направления вращения двигателя. Сначала определяется номер сектора n, в котором находится заданный пространственный вектор. Затем на каждом периоде ШИМ рассчитываются значения γ 1 и γ 2 по формулам (2.26). По ним определяются уровни переключения УП 1= γ 1 и УП 2= γ 1 + γ 2 , при сравнении которых с пилообразным сигналом осуществляется переключение базовых векторов. Алгоритм переключений представляет собой следующую последовательность действий:
‒ после определения номера сектора n в начале каждого периода ШИМ устанавливается состояние инвертора, соответствующее исходному базовому вектору (для сектора 2 – это вектор 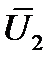 );
);
‒ при первом сравнении с уровнем УП 1 осуществляется переход ко второму базовому вектору (для сектора 2 – это вектор  );
);
‒ первое сравнение с уровнем УП 2 вызывает переход к нулевому вектору  . При этом в соответствии с табл. 2.2. включается тот нулевой вектор, который требует минимального переключения ключей инвертора по отношению к предыдущему состоянию вентилей;
. При этом в соответствии с табл. 2.2. включается тот нулевой вектор, который требует минимального переключения ключей инвертора по отношению к предыдущему состоянию вентилей;
‒ при втором сравнении с УП 2 восстанавливается предыдущее состояние (для сектора 2 – это вектор  );
);
‒ при втором сравнении с УП 1 осуществляется возврат к начальному состоянию (для сектора 2 – это вектор 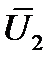 ).
).
Входными сигналами для преобразователя частоты с автономным инвертором являются задаваемые из системы управления электропривода угол поворота обобщенного вектора, вращающегося с синхронной скоростью в полярной системе координат, и требуемое значение амплитуды U m пространственного вектора напряжения  . Микропроцессорная система в реальном времени определяет номер сектора n и внутри секторный угол поворота θ, после чего производит расчет точек переключения в соответствии с выбранным алгоритмом.
. Микропроцессорная система в реальном времени определяет номер сектора n и внутри секторный угол поворота θ, после чего производит расчет точек переключения в соответствии с выбранным алгоритмом.
Один из вариантов функциональной схемы микропроцессорной системы управления векторной ШИМ представлен на рис. 2.13.
Рис. 2.13. Функциональная схема микропроцессорной системы управления векторной ШИМ
В состав микропроцессорной системы управления входят следующие основные блоки: формирователь угла поворота θ, определитель номера
сектора, вычислитель уровней переключений УП 1 и УП 2, блок сравнения, генератор пилообразного напряжения (ГПН), генератор синхронизирующих импульсов (ГСИ), блок памяти и выходные драйверы.
Формирователь угла поворота θ осуществляет формирование угла поворота пространственного вектора в полярной системе координат и его изменение в функции частоты f задающего воздействия c целью регулирования выходной частоты АИН. Работа блока сводится к расчету дискретного угла поворота пространственного вектора внутри сектора Δθ = 360/ k, где k – целое число, соответствующее количество периодов ШИМ за один период несущей частоты, и определение нового значения угла поворота θ i =θ i-1 +Δθ. Увеличение угла поворота на величину Δθ осуществляется под действием синхроимпульсов f син, формируемых в моменты перехода пилообразного напряжения ШИМ через нулевой уровень. При выполнении условия θ i≥ 360°, что соответствует одному обороту пространственного вектора вокруг своей оси в полярной системе координат, осуществляется установка начального угла поворота θ 0=0°.
Вычислитель уровней УП 1, УП 2 синхронно с приходом синхроимпульсов f син осуществляет расчет относительных продолжительностей включения γ1 и γ2 базовых векторов по формулам (2.26) и определяет уровни переключения УП 1= γ1 и УП 2= γ2 .В блоке сравнения происходит сравнение уровней переключения УП 1 и УП 2 с пилообразным напряжением, формируемым ГПН, с целью нахождения временных интервалов для переключения базовых векторов внутри сектора. Блок памяти представляет собой постоянное запоминающее устройство, в котором хранятся коды состояния ключей инвертора для каждого сектора, переключаемых в функции выходных сигналов блока сравнения. Порядок чередования выходных фаз инвертора изменяется логическим сигналом «Направление вращения», воздействующим на определитель номера сектора и блок памяти, в котором записываются коды состояния ключей инвертора при вращении пространственного вектора, как по часовой, так и против часовой стрелки. Управление силовыми ключами инвертора осуществляется при помощи драйверов.
Формирование трехфазной системы фазных напряжений на выходе преобразователя показано на рис. 2.14. В верхней части рисунка изображен пилообразный сигнал u оп и указаны значения угла поворота θ на каждом
периоде ШИМ. Отмечены уровни переключения УП 1 и УП 2, а также замкнутые состояния ключей на каждом периоде ШИМ. Построение произведено для второго сектора n = 2 и глубины регулирования μ = 0,7 в предположении, что пространственный вектор  поворачивается на 60 ° за шесть периодов ШИМ. Результаты расчета в соответствии с выражениями (2.26), (2.20) для заданных значений параметров n и m приведены в табл. 2.5.
поворачивается на 60 ° за шесть периодов ШИМ. Результаты расчета в соответствии с выражениями (2.26), (2.20) для заданных значений параметров n и m приведены в табл. 2.5.
Рис. 2.14. Формирование напряжения на выходе АИН с векторной ШИМ во втором секторе при μ =0,7
Поскольку в реальном случае частота ШИМ составляет килогерцы, т.е. число периодов ШИМ за время поворота вектора на 60 ° многократно больше показанного на рис. 2.13, то среднее фазное напряжение, полученное в соответствии с описанным алгоритмом, обеспечивает практически синусоидальную форму токов на нагрузке АИН.
Одним из важнейшим преимуществ метода формирования фазных напряжений с помощью пространственного вектора является уменьшение числа переключений на периоде ШИМ с 6-и до 4-х по сравнению с методом формирования средних напряжений на выводах по отношению к средней точке источника питания и, как следствие, сокращения на 30 % динамических потерь в ключевых элементах инвертора. Кроме этого при данном способе управления удается получить фазное и линейное напряжения на выходе АИН на 13,4 % больше, чем при формировании средних напряжений на выводах по отношению к средней точке при неизменном напряжении питания Ud на входе инвертора.
Т а б л и ц а 2.5.
Результаты расчета γ 1, γ 2, γ 0 в соответствии с выражениями (2.26), (2.20) для заданных значений параметров n и m
| Величина | Значение величины | ||||||
| θ | 60 º | 70 º | 80 º | 90 º | 100 º | 110 º | 120 º |
| γ 1 | 0,6 | 0,53 | 0,45 | 0,35 | 0,24 | 0,12 | |
| γ 2 | 0,12 | 0,24 | 0,35 | 0,45 | 0,53 | 0,6 | |
| γ 0 | 0,4 | 0,35 | 0,31 | 0,3 | 0,31 | 0,35 | 0,4 |
