Проверка правильности принятой гипотезы

Расчет эмпирических характеристик надежности

Интервал наработки 0…24000 часов разбиваем на разряды по правилу Старджена:

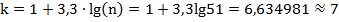
Где k—число разрядов, n – число отказавших изделий.

 

Число разрядов принимаем равным 7 с интервалом .

По формулам вычисляем в каждом разряде значения

fi(t),

 

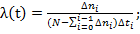
Результаты расчетов представляются в табличном виде

№ инт.
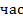
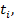
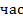
						8,3
						2,9	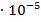0,967
						2,7	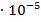0,853
						1,3	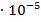0,76
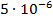
						6,9	0,72
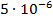
						7,3	0,68

 

По данным таблицы строятся гистограммы эмпирического распределения.

Рисунок 1 плотность распределения

Рисунок 2 интенсивность отказов

Рисунок 3 вероятность безотказной работы

2 Выбор теоретического закона распределения

Так как отказы носят усталостный характер, при котором каждое воздействие внешней нагрузки приводит к накоплению повреждений в материале лопаток 1-ой ступени двигателя, то выбираем логарифмический нормальный закон распределения отказов.

Определение параметров закона распределения

Параметры закона распределения можно найти методом разделяющих разбиений.

Выберем значения наработки:

Находим значения стандартной нормальной функции распределения

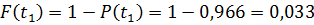
По таблице значений стандартной нормальной функции распределения находим значения квантилей Z, соответствующих значениям F(ti):

; ;

Находим параметры закона и :

 

Проверка правильности принятой гипотезы

Проверка осуществляется с помощью критерия Пирсона , рассчитанного по выражению:

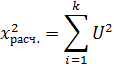
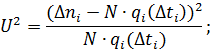
Где 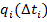– теоретическая вероятность отказа в интервале .

Число разрядов при расчете критерия Пирсона на единицу больше числа разрядов разбиения вариационного ряда k, так как добавляется интервал до . Результаты расчетов приведены в таблице:

Таблица 2 – расчет критерия Пирсона

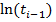№	час	час	, час	час
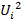
		8,29405			0,0139	2,085	2,915	4,0754
	8,294	8,987197			0,0443	6,645	10,355	16,136
	8,9872	9,392662			0,0588	8,82	5,18	3,0422
	9,393	9,680344			0,0618	9,27	-3,27	1,1535
	9,68	10,08581			0,1124	16,86	-10,86	6,9952
	10,086	10,23996			0,05	7,5	-4,5	2,7
	10,24	>>28000	----		0,6588	98,82	0,18	0,0003

 

Вывод: согласно расчетам критерия Пирсона установлено, что Вейбуловское распределение описывает отказ усталостного разрушения лопаток 1-ой ступени двигателя Д-18Т более достоверно с меньшими погрешностями.

 

3 Определение точности параметров распределения

Верхние и нижние границы доверительных интервалов для параметров и вычисляем по следующим формулам:

; ;

; ;

Где —квантиль нормального распределения. Для

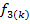и находятся по таблице значений этих коэффициентов в зависимости от величины .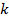

; ; ;

= 0,8712;

= 1,2695;

;

;

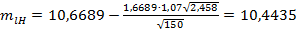Таким образом, интервал (0,8712; 1,2695) с доверительной вероятностью 90% покрывает истинное значение параметра , а интервал (10,4435; 10,8943) покрывает истинное значение параметра .

 

4 Построение графиков теоретического распределения

Построение графиков распределения производим для диапазона часов. Нижнее значение соответствует и , а верхнее значение соответствует и .

Данные вносим в таблицу 3:

Таблица 3 – Расчет теоретических характеристик

t,ч
	0,9928	0,9938
	0,9525	0,9332
	0,8849	0,881
	0,8106	0,8315
	0,73	0,7823
	0,6591	0,7357
	0,591	0,695

 

По данным таблицы 3 строим график:

 

Рисунок 4 Вероятность безотказной работы

5 Оценка уровня надежности

Для заданных данных: нормативное значение вероятности безотказной работы и наработка до отказа часов, оценим уровень надежности изделия при этой наработке.

Найдем пределы и :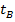

Найдем значения стандартной нормальной функции распределения:

;

;

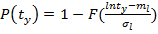=-1,405

 

 

Вывод: уровень надежности соответствует нормативному значению, так как фактическое значение наработки в интервале (5767,068…15839,91) превышает нормативные значения наработки t= 3000 часов, при заданной вероятности безотказной работы P(t)=0,92.

Список использованных источников

1. Кочуров В.А., Новиков Г.А., примеры расчета характеристик надежности авиационной техники [текст]: методическое указания / В.А. Кочуров, Г.А. Новиков, Самара: СГАУ, 2002г. 48 стр.