Содержание
1.Функция Бесселя……………………………………………………………..2
2.Бесселевы функции с любым индексом ……………………………………2
3. Бесселевы функции первого рода………………………………………….5
4. Бесселевы функции второго рода………………………………………….7
5.Общее решение уравнения Бесселя………………………………………..7
6. Формулы приведения для бесселевых функций………………………….9
7. Бесселевы функции с полуцелым индексом............................................. 11
8. Интегральное представление бесселевых функций с целым индексом.. 13
9. Ряды Фурье-Бесселя................................................................................. 17
10.Свойства……………………………………………………………………..21
11. Асимптотическое представление бесселевых функций с целым индексом для больших значений аргумента...................................................................................... 22
Список литературы...................................................................................... 30
Функции Бесселя
Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:
где α — произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя — функции целых порядков.Хотя α, и − α порождают одинаковые уравнения, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по α).
Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.
Применения: Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:
- электромагнитные волны в цилиндрическом волноводе;
- теплопроводность в цилиндрических объектах;
Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.
Определения: Поскольку приведённое уравнение является уравнением второго порядка, у него должно быть два линейно независимых решения. Однако в зависимости от обстоятельств выбираются разные определения этих решений.
Бесселевы функции с любым индексом
Уравнение Лапласа в цилиндрических координатах
Чтобы объяснить происхождение бесселевых функций, рассмотрим уравнение Лапласа в пространстве:
. (1)
Если перейти к цилиндрическим координатам по формулам:
, 
, 
,
то уравнение (1) примет следующий вид:
. (2)
Поставим задачу: найти все такие решения уравнения, которые могут быть представлены в виде произведения трех функций, каждая из которых зависит только от одного аргумента, то есть найти все решения вида:
,
где 
, 
, 
предполагаются дважды непрерывно дифференцируемыми.
Пусть 
есть решение упомянутого вида. Подставляя его в (2), получим:
,
откуда (после деления на 
)
.
Записав это в виде:
,
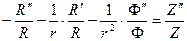найдем, что левая часть не зависит от 
, правая не зависит от 
, 
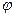; следовательно, общая величина этих выражений есть некоторая постоянная 
. Отсюда:
; 
;
; 
;
.
В последнем равенстве левая часть не зависит от 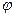, правая не зависит от 
; следовательно, общая величина этих выражений есть некоторая постоянная 
. Отсюда:
, 
;
, 
.
Таким образом, , , должны удовлетворять линейным дифференциальным уравнениям второго порядка:
,
(3)
, ,
из которых второе и третье есть простейшие линейные уравнения с постоянными коэффициентами, а первое является линейным уравнением с переменными коэффициентами нового вида.
Обратно, если , , удовлетворяют уравнениям (3), то 
есть решение уравнения (2). В самом деле, подставляя в левую часть (2) и деля затем на , получим:
.
Таким образом, общий вид всех трех решений уравнения (2), которые являются произведением трех функций, каждая из которых зависит от одного аргумента, есть , где , , – любые решения уравнений (3) при любом выборе чисел , .
Первое из уравнений (3) в случае 
, 
называется уравнением Бесселя. Полагая в этом случае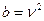 
, обозначая независимую переменную буквой 
(вместо ), а неизвестную функцию – буквой 
(вместо ), найдем, что уравнение Бесселя имеет вид:
. (4)
Это линейное дифференциальное уравнение второго порядка с переменными коэффициентами играет большую роль в приложениях математики. Функции, ему удовлетворяющие, называются бесселевыми, или цилиндрическими, функциями.