Вопросы к экзамену по ВМ 2009 ГФ
ЧИСЛА.
Числа натуральные, целые, действия с числами, простые и составные числа, Десятичные дроби: Рациональные, иррациональные, действительные числа. Действия со степенями, свойства степени, арифметический корень.
Комплексные числа в алгебраической форме, действия с ними. Комплексная плоскость, геометрическая интерпретация комплексного числа, полярные координаты точки, аргумент, главное значение аргумента комплексного числа,
тригонометрическая форма, показательная форма комплексного числа, формулы Эйлера. Действия над комплексными числами.
Проценты, основные задачи на проценты.
Множества. Операции над множествами. Два равных множества, подмножество, объединение, пересечение, разность, универсальное множество, дополнение,. Мощность множества.
Матрицы. Задача приводящая к понятию матриц. Определение матриц, частные виды матриц. Действия с матрицами.
Определители. Определители второго и третьего порядков. Вычисление определителей. Основные свойства определителей. Минор и алгебраическое дополнение элементов матрицы. Теорема Лапласа. Обратная матрица. Ранг матрицы. Элементарные преобразования матриц. Методы вычислений ранга матрицы.
Системы линейных алгебраических уравнений. Решение систем линейных алгебраических уравнений методом Крамера, матричным методом, методом Гаусса. Решение систем в общем виде.
Метод координат. Числовая прямая, координаты точки, направленный отрезок, (длина, величина, свойства длины и величины), координаты точки. Расстояние между двумя точками на прямой. Прямоугольные координаты на плоскости. Полярные координаты на плоскости. Декартова система координат в пространстве.
Прямая на плоскости. Задача о расстоянии между двумя точками, задача о делении отрезка в данном отношении.
Уравнения прямой на плоскости: а) с угловым коэффициентом, б) уравнение прямой, проходящей ч\з две заданные точки, в) в отрезках на осях координат,
г) параметрические уравнения прямой, д) общее уравнение прямой, е) нормальное уравнение прямой. Кривые второго порядка, их канонические уравнения.
Определение функции. Способы задания, графики элементарных функций, область определения, область значений функции. Монотонности функции. Четность, нечетность, периодичность.
Понятие предела функции в точке. Замечательные пределы. Непрерывность функции в точке. Характеристика точек разрыва (I рода, II рода).
Производная функции. Определение производной функции в точке, ее геометрический и физический смысл, таблица производных, правила дифференцирования. Производная сложной функции.
Наибольшее и наименьшее значения функции на отрезке. Экстремум функции.
Необходимое и достаточное условие монотонности функции.
Производные высших порядков. Выпуклость графика функции., тоски перегиба. Дифференциал функции. Приложение дифференциала для приближенных вычислений.
Приложение производных к исследованию функций и построению графиков функций.
I. Неопределенный интеграл
Определение
2. Основные свойства неопределенного интеграла
3. Непосредственное интегрирование,
таблица интегралов №1.
4. Подведением под знак дифференциала, метод замены переменной или метод подстановки. таблица интегралов №2.
5. Метод интегрирования по частям.
6. Интегрирование рациональных дробей
6.1. Простейшими элементарными дробями называются дроби следующего вида:
I.  ;
;
II.  ,
,  >1, целое;
>1, целое;
III.  , где
, где  < 0, т.е. квадратный трехчлен не имеет действительных корней;
< 0, т.е. квадратный трехчлен не имеет действительных корней; 
IV  , где дискриминант D=
, где дискриминант D=  < 0, т.е. квадратный трехчлен не имеет действительных корней.
< 0, т.е. квадратный трехчлен не имеет действительных корней.
6.2. Интегралы от простейших рациональных дробей I и II вычисляются как табличные:
I.  .
.
II.  :
:
III.  =
=  .
.
Интегралы от рациональной дроби IV 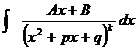 вычисляются аналогично с помощью подстановки
вычисляются аналогично с помощью подстановки 
 ,
,  .
.
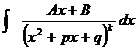 =
= 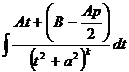 =
= 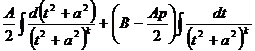 .
.
7.  ,
,
8.  .
.
9.  ,
, 
10.Tригонометрические подстановки ( ,
, 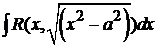 ,
,  .
.
II. Определенный интеграл.
1. Определение определенного интеграла.
2. основные свойства определенного интеграла.
3. Формула Ньютона - Лейбница 
4. Замена переменной, интегрирование по частям.
5. Несобственные интегралы.
5.1.Несобственные интегралы по бесконечному интервалу (I рода).
5.2. Несобственные интегралы от неограниченных функций
6. Приложения определенного интеграла.
Вычисление площади плоской фигуры
6.2.. Вычисление длины дуги кривой
6.3. Вычисление о бъем тела
III. ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
1. Определение функции двух переменных.Область определения, множество значений функции двух переменных.
2. Дифференцирование функции двух переменных.
2.1. Частные производные функции двух переменных, полный дифференциал.
2.2. Частные приращения функции Dx z
2.3. Частные производные высших порядков. Определение частных производных второго порядка от функции z = f (x; y).
3. Приложения функции двух переменных и ее производных.
3.1. Производная от функции u(x; y; z) по направлению вектора.
3.2. Градиент функции.
3.3. Касательная плоскость к поверхности в точке M0. Уравнение Касательной плоскости.
3.4.Определение Нормали к поверхности в точке M 0. Уравнение Нормали.
3.5. Э кстремум функции двух переменных.
Определение максимума (минимум) в точке M0(x0;y0)
Теорема. (Необходимые условия экстремума ).
Стационарные и критические точки функции..
Теорема. (Достаточные условия экстремума ). Пусть M0 (x0; y0) - критическая точка функции z = f (x; y). Пусть в некоторой ее окрестности частные производные первого и второго порядка непрерывны. Обозначим значения вторых производных функции z = f (x; y) в точке M0 через
A = 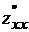 (M 0), B =
(M 0), B =  (M 0), C =
(M 0), C =  (M 0).
(M 0).
Составим определитель второго порядка:
D =  = A C -
= A C -  .
.
Тогда:
1. если D > 0, то функция z имеет в точке M 0 экстремум, причем:
а) если A < 0, - максимум,
б) если A > 0, - минимум,
2. если D < 0, то функция z не имеет в точке M 0 экстремума,
3. если D = 0, то вопрос о существовании в точке M 0 экстремума функции z остается открытым, требуются дополнительны
Литература:
1 Н.С. Пискунов. «Диф. уравнения и интегр.исчисления», т.2, 1985г.
2 В.С Шипачев. «Высшая математика», М.1999г.
3 В.С Шипачев. «Сборник задач по высшей математике», М.1999г.
4 А.Н. Колесников. «Краткий курс математики для экономистов». М.1997г.
5 Е.В. Шикин, Г.Е.Шикина «Гуманитариям о математике», АГАР, 1999г.
6 И.И.Баврин «Высшая математика». М.2000г.
7 Д.Пидоу «Геометрия и искусство», М.1979г.
8 Ю.П.Попов, Ю.В.Пухначев «Математика вобразах», М.1989г.
9 Шафаревич, сочинение в трех томах, М.1994г.
10 А.Н.Бородин «Элементарный курс теории вероятностей», С-П. 1999г.
Лектор старший преподаватель Матвеенко Г.М.