I. Для студентов бакалавриата направлений
| Экономика
| Менеджмент
| | Контрольная работа №2 (э)
| Контрольная работа №2 (м)
| | ВАРИАНТ 1
(для студентов, номера личных дел которых
оканчиваются цифрой 1)
| 1.Найти предел:
 2. Составить уравнения касательных к графику функции
2. Составить уравнения касательных к графику функции  параллельных параллельных
| 1. Даны матрицы  , ,  . Найти определитель матрицы . Найти определитель матрицы  . .
| прямой, проходящей через точки (1; 8) и (–1; –2). Сделать чертеж.
3. Исследовать функцию  и и
| 2. Найти предел:

| построить схематично ее график.
4.Вычислить определенный интеграл

| 3. Составить уравнения касательных к графику функции  параллельных прямой, проходящей через точки (1; 8) и (–1; –2). Сделать чертеж. параллельных прямой, проходящей через точки (1; 8) и (–1; –2). Сделать чертеж.
| 5.Решить дифференциальное уравнение:
 6.Вычислить площадь фигуры, ограниченной линиями:
6.Вычислить площадь фигуры, ограниченной линиями:
| 4. Исследовать функцию  и построить схематично ее график. и построить схематично ее график.
|  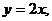  7.Экспериментальные данные о значениях переменных х и y приведены в таблице:
7.Экспериментальные данные о значениях переменных х и y приведены в таблице:
| 5. Найти неопределенный интеграл:

| 
|
| 1,5
|
| 2,5
|
| 3,5
| | 
|
|
|
|
|
|
| | | | | | | | | | | В результате их выравнивания получена функция  Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью
| 6. Вычислить определенный интеграл

|  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
| 7.Вычислить площадь фигуры, ограниченной линиями:
 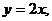 
|
| Экономика
| Менеджмент
| | Контрольная работа №2 (э)
| Контрольная работа №2 (м)
| | ВАРИАНТ 3
(для студентов, номера личных дел которых
оканчиваются цифрой 3)
| 1. Найти предел:
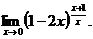 2.Составить уравнения касательных к графику функции
2.Составить уравнения касательных к графику функции  образующих с образующих с
| 1.Методом обратной матрицы решить систему линейных уравнений:

| осью Ох угол  . Сделать чертеж.
3. Исследовать функцию . Сделать чертеж.
3. Исследовать функцию  и и
| 2. Найти предел:
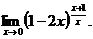
| построить схематично ее график.
4.Вычислить определенный интеграл

| 3. Составить уравнения касательных к графику функции  образующих с осью Ох угол образующих с осью Ох угол  . Сделать чертеж. . Сделать чертеж.
| 5.Решить дифференциальное уравнение:

| 4. Исследовать функцию  и построить схематично ее график. и построить схематично ее график.
| 6.Вычислить площадь фигуры, ограниченной линиями:
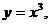   
| 5. Найти неопределенный интеграл:
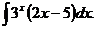
| 7. Экспериментальные данные о значениях переменных х и y приведены в таблице:

|
|
|
|
|
|
| 
| 1,3
| 1,8
| 2,2
| 2,3
| 2,6
|
| В результате их выравнивания получена
| 6. Вычислить определенный интеграл

| функция  Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
| 7.Вычислить площадь фигуры, ограниченной линиями:
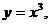   
| | Экономика
| Менеджмент
| | Контрольная работа №2 (э)
| Контрольная работа №2 (м)
| | ВАРИАНТ 4
(для студентов, номера личных дел которых
оканчиваются цифрой 4)
| 1. Найти предел:
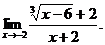
| 1.Методом Гаусса решить систему линейных уравнений:

| 2.Составить уравнения касательных к графику функции 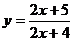 , перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж. , перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж.
| 2. Найти предел:
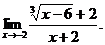
| 3. Исследовать функцию  и построить схематично ее график.
4.Найти неопределенный интеграл: и построить схематично ее график.
4.Найти неопределенный интеграл:
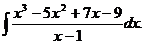
| 3. Составить уравнения касательных к графику функции 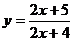 , перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж. , перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж.
| 5.Решить дифференциальное уравнение:

| 4. Исследовать функцию  и построить схематично ее график. и построить схематично ее график.
| 6.Вычислить площадь фигуры, ограниченной линиями:
  7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| 5.Найти неопределенный интеграл:
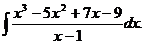
| 
|
| 4,5
|
| 5,5
|
| 
| 0,8
| 0,5
| 0,2
| 0,4
| 0,9
| В результате их выравнивания получена функция  Используя метод Используя метод
| 6. Вычислить определенный интеграл

| наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
| 7.Вычислить площадь фигуры, ограниченной линиями:
 
| | Экономика
| Менеджмент
| | Контрольная работа №2 (э)
| Контрольная работа №2 (м)
| | ВАРИАНТ 5
(для студентов, номера личных дел которых
оканчиваются цифрой 5)
| 1. Найти предел:

| 1.Решить матричное уравнение
 ,
где ,
где    . .
| 2.Хорда параболы  соединяет точки с абсциссами соединяет точки с абсциссами  и и  . Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж. . Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж.
| 2. Найти предел:

| 3. Исследовать функцию  и построить схематично ее график.
4.Найти неопределенный интеграл: и построить схематично ее график.
4.Найти неопределенный интеграл:

| 3. Хорда параболы  соединяет точки с абсциссами соединяет точки с абсциссами  и и  . Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж. . Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж.
| 5.Решить дифференциальное уравнение:

| 4. Исследовать функцию  и построить схематично ее график. и построить схематично ее график.
| 6.Вычислить площадь фигуры, ограниченной линиями:
  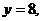 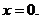
| 5. Найти неопределенный интеграл:

| 7. Экспериментальные данные о значениях переменных х и y приведены в таблице:

| –2
| –1
|
|
|
| 
|
|
|
| 0,5
| 0,2
| В результате их выравнивания получена функция 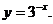 Используя метод наимень- Используя метод наимень-
| 6. Вычислить определенный интеграл:

| ших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
| 7. Вычислить площадь фигуры, ограниченной линиями:
  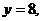 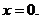
|
| Экономика
| Менеджмент
| | Контрольная работа №2 (э)
| Контрольная работа №2 (м)
| | ВАРИАНТ 6
(для студентов, номера личных дел которых
оканчиваются цифрой 6)
| 1. Найти предел:

| 1.Решить матричное уравнение

| 2.Составить уравнения касательных к графику функции 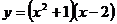 в точках ее пересечения с осями координат. Сделать чертеж. в точках ее пересечения с осями координат. Сделать чертеж.
| 2. Найти предел:

| 3. Исследовать функцию 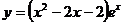 и построить схематично ее график. и построить схематично ее график.
| 3. Составить уравнения касательных к графику функции 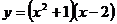 в в
| 4.Найти неопределенный интеграл:

| точках ее пересечения с осями координат. Сделать чертеж.
4. Исследовать функцию
| 5. Решить дифференциальное уравнение:

| 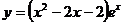 и построить схематично ее график.
5.Найти неопределенный интеграл: и построить схематично ее график.
5.Найти неопределенный интеграл:
| 6.Вычислить площадь фигуры, ограниченной линиями:
  
|  6.Вычислить определенный интеграл:
6.Вычислить определенный интеграл:
| 7. Экспериментальные данные о значениях переменных х и y приведены в таблице:

| –4
| –3
| –2
| –1
|
|
| 
| –1,2
| –0,71
| –0,01
| 0,53
| 0,82
| 0,92
| В результате их выравнивания получена функция  Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж
|  7. Вычислить площадь фигуры, ограниченной линиями:
7. Вычислить площадь фигуры, ограниченной линиями:
  
|
| Экономика
| Менеджмент
| | Контрольная работа №2 (э)
| Контрольная работа №2 (м)
| | ВАРИАНТ 8
(для студентов, номера личных дел которых
оканчиваются цифрой 8)
| 1. Найти предел:
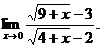 2.Составить уравнения касательных к графику функции
2.Составить уравнения касательных к графику функции  которые па- которые па-
| 1.Методом обратной матрицы решить систему линейных уравнений:

| раллельны прямой 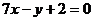 . Сделать чертеж.
3.Исследовать функцию . Сделать чертеж.
3.Исследовать функцию  и построить схематично ее график. и построить схематично ее график.
| 2. Найти предел:
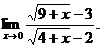
| 4.Вычислить определенный интеграл:
 5. Решить дифференциальное уравнение:
5. Решить дифференциальное уравнение:
| 3. Составить уравнения касательных к графику функции  которые параллельны прямой которые параллельны прямой 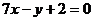 . Сделать чертеж. . Сделать чертеж.
| 
| 4. Исследовать функцию  и построить схематично ее график. и построить схематично ее график.
| 6.Вычислить площадь фигуры, ограниченной линиями:
  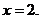
| 5.Найти неопределенный интеграл:

| 7. Экспериментальные данные о значениях переменных х и y приведены в таблице:

| –3
| –1
|
|
|
| 
| –1,3
| –2,6
| 3,3
| 0,8
| 0,8
| В результате их выравнивания получена
| 6. Вычислить определенный интеграл:

| функция  Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
| 7. Вычислить площадь фигуры, ограниченной линиями:
  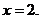
| | Экономика
| Менеджмент
| | Контрольная работа №2 (э)
| Контрольная работа №2 (м)
| | ВАРИАНТ 9
(для студентов, номера личных дел которых
оканчиваются цифрой 9)
| 1. Найти предел:
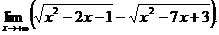 2.Составить уравнения касательных к графику функции
2.Составить уравнения касательных к графику функции  в точках ее пе- в точках ее пе-
| 1.Методом Гаусса решить систему линейных уравнений:

| ресечения с прямой, проходящей через точки с координатами (1; 5) и (–1; –5). Сделать чертеж.
3. Исследовать функцию  и построить схематично ее график.
4.Найти неопределенный интеграл: и построить схематично ее график.
4.Найти неопределенный интеграл:
| 2. Найти предел:
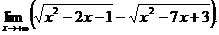 3. Составить уравнения касательных к графику функции
3. Составить уравнения касательных к графику функции  в точках ее в точках ее
|  5. Решить дифференциальное уравнение:
5. Решить дифференциальное уравнение:

| пересечения с прямой, проходящей через точки с координатами (1; 5) и (–1; –5). Сделать чертеж.
| 6.Вычислить площадь фигуры, ограниченной линиями
 
| 4. Исследовать функцию  и построить схематично ее график. и построить схематично ее график.
| 7. Экспериментальные данные о значениях переменных х и y приведены в таблице:

|
|
|
|
|
| 
| 0,91
| 1,02
| 1,26
| 1,30
| 1,41
| В результате их выравнивания получена
| 5. Найти неопределенный интеграл:

| функция  Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры (найти параметры
| 6. Вычислить определенный интеграл:

| | а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
| 7. Вычислить площадь фигуры, ограниченной линиями
 
|
| Экономика
| Менеджмент
| | Контрольная работа №2 (э)
| Контрольная работа №2 (м)
| | ВАРИАНТ 10
(для студентов, номера личных дел которых
оканчиваются цифрой 0)
| 1. Найти предел:

| 1.Найти матрицу  , где , где
 
| 2.Составить уравнения касательных к графику функции 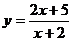 , перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7). Сделать чертеж. , перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7). Сделать чертеж.
| 2. Найти предел:

| 3. Исследовать функцию  и построить схематично ее график.
4.Найти неопределенный интеграл: и построить схематично ее график.
4.Найти неопределенный интеграл:
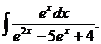
| 3. Составить уравнения касательных к графику функции 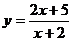 , перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7).. Сделать чертеж. , перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7).. Сделать чертеж.
| 5. Решить дифференциальное уравнение:

| 4. Исследовать функцию  и построить схематично ее график. и построить схематично ее график.
| 6.Вычислить площадь фигуры, ограниченной линиями:
  7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
| 5. Найти неопределенный интеграл:
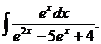
| 
|
| 1,5
|
| 2,5
|
| 
| 2,2
| 3,9
| 5,8
| 8,8
| 12,3
| В результате их выравнивания получена функция 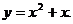 Используя метод наи- Используя метод наи-
| 6. Вычислить определенный интеграл:
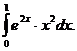
| меньших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
| 7. Вычислить площадь фигуры, ограниченной линиями:
 
|
|
Поиск по сайту:
|
 2. Составить уравнения касательных к графику функции
2. Составить уравнения касательных к графику функции  параллельных
параллельных
 ,
,  . Найти определитель матрицы
. Найти определитель матрицы  .
.
 и
и


 параллельных прямой, проходящей через точки (1; 8) и (–1; –2). Сделать чертеж.
параллельных прямой, проходящей через точки (1; 8) и (–1; –2). Сделать чертеж.
 6.Вычислить площадь фигуры, ограниченной линиями:
6.Вычислить площадь фигуры, ограниченной линиями:
 и построить схематично ее график.
и построить схематично ее график.

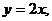
 7.Экспериментальные данные о значениях переменных х и y приведены в таблице:
7.Экспериментальные данные о значениях переменных х и y приведены в таблице:


 (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.

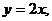

 2. Составить уравнения касательных к графику функции
2. Составить уравнения касательных к графику функции  проведенных в точках ее пересечения с прямой
проведенных в точках ее пересечения с прямой  Сделать чертеж.
Сделать чертеж.

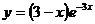 и построить схематично ее график.
4.Вычислить определенный интеграл
и построить схематично ее график.
4.Вычислить определенный интеграл

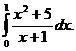 5.Решить дифференциальное уравнение:
5.Решить дифференциальное уравнение:
 проведенных в точках ее пересечения с прямой
проведенных в точках ее пересечения с прямой  Сделать чертеж.
Сделать чертеж.
 6.Вычислить площадь фигуры, ограниченной линиями:
6.Вычислить площадь фигуры, ограниченной линиями:
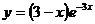 и построить схематично ее график.
и построить схематично ее график.


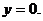 7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
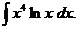
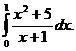
 (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.


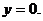
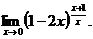 2.Составить уравнения касательных к графику функции
2.Составить уравнения касательных к графику функции  образующих с
образующих с

 . Сделать чертеж.
3. Исследовать функцию
. Сделать чертеж.
3. Исследовать функцию  и
и
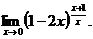

 образующих с осью Ох угол
образующих с осью Ох угол  . Сделать чертеж.
. Сделать чертеж.

 и построить схематично ее график.
и построить схематично ее график.
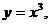



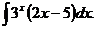

 Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
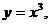



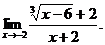

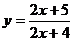 , перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж.
, перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж.
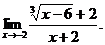
 и построить схематично ее график.
4.Найти неопределенный интеграл:
и построить схематично ее график.
4.Найти неопределенный интеграл:
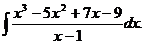
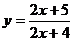 , перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж.
, перпендикулярных прямой, проходящей через точки (1; 1) и (–1; 0). Сделать чертеж.

 и построить схематично ее график.
и построить схематично ее график.

 7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
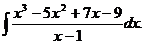

 (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.



 ,
где
,
где 

 .
.
 соединяет точки с абсциссами
соединяет точки с абсциссами  и
и  . Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж.
. Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж.

 и построить схематично ее график.
4.Найти неопределенный интеграл:
и построить схематично ее график.
4.Найти неопределенный интеграл:

 соединяет точки с абсциссами
соединяет точки с абсциссами  и
и  . Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж.
. Составить уравнение касательной к параболе, параллельной этой хорде. Сделать чертеж.

 и построить схематично ее график.
и построить схематично ее график.


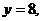
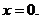


 (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.


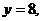
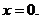


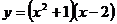 в точках ее пересечения с осями координат. Сделать чертеж.
в точках ее пересечения с осями координат. Сделать чертеж.

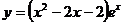 и построить схематично ее график.
и построить схематично ее график.
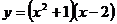 в
в


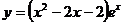 и построить схематично ее график.
5.Найти неопределенный интеграл:
и построить схематично ее график.
5.Найти неопределенный интеграл:



 6.Вычислить определенный интеграл:
6.Вычислить определенный интеграл:
 7. Вычислить площадь фигуры, ограниченной линиями:
7. Вычислить площадь фигуры, ограниченной линиями:



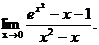 2.Составить уравнение касательной к графику функции
2.Составить уравнение касательной к графику функции 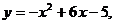 перпендикулярной прямой
перпендикулярной прямой

 . Сделать чертеж.
3.Исследовать функцию
. Сделать чертеж.
3.Исследовать функцию  и построить схематично ее график.
и построить схематично ее график.
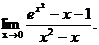

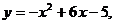 перпендикулярной прямой
перпендикулярной прямой  . Сделать чертеж.
. Сделать чертеж.
 .
.
 и построить схематично ее график.
и построить схематично ее график.

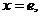

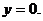


 Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.

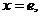

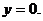
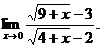 2.Составить уравнения касательных к графику функции
2.Составить уравнения касательных к графику функции  которые па-
которые па-

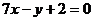 . Сделать чертеж.
3.Исследовать функцию
. Сделать чертеж.
3.Исследовать функцию  и построить схематично ее график.
и построить схематично ее график.
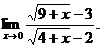
 5. Решить дифференциальное уравнение:
5. Решить дифференциальное уравнение:
 которые параллельны прямой
которые параллельны прямой 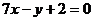 . Сделать чертеж.
. Сделать чертеж.

 и построить схематично ее график.
и построить схематично ее график.


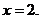


 Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.


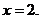
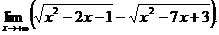 2.Составить уравнения касательных к графику функции
2.Составить уравнения касательных к графику функции  в точках ее пе-
в точках ее пе-

 и построить схематично ее график.
4.Найти неопределенный интеграл:
и построить схематично ее график.
4.Найти неопределенный интеграл:
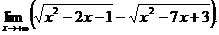 3. Составить уравнения касательных к графику функции
3. Составить уравнения касательных к графику функции  в точках ее
в точках ее
 5. Решить дифференциальное уравнение:
5. Решить дифференциальное уравнение:



 и построить схематично ее график.
и построить схематично ее график.

 Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью  (найти параметры
(найти параметры




 , где
, где


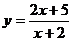 , перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7). Сделать чертеж.
, перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7). Сделать чертеж.

 и построить схематично ее график.
4.Найти неопределенный интеграл:
и построить схематично ее график.
4.Найти неопределенный интеграл:
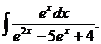
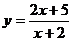 , перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7).. Сделать чертеж.
, перпендикулярных прямой, проходящей через точки (0; 3) и (1; 7).. Сделать чертеж.

 и построить схематично ее график.
и построить схематично ее график.

 7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
7. Экспериментальные данные о значениях переменных х и y приведены в таблице:
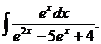
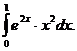
 (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
(найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.




 Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью Используя метод
Используя метод Используя метод
Используя метод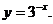 Используя метод наимень-
Используя метод наимень- Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью
Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 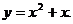 Используя метод наи-
Используя метод наи-