Наиболее широкоприменяемая схема низкочастотной коррекции использует цепочку 
. Сущность уменьшения спада вершины поясним на эквивалентной схеме.
В эквивалентной схеме транзистор представлен генератором 
, что допустимо, если пренебречь в эквивалентной схеме обратной связью через rэ, сопротивлением rэ и посчитать 
, то есть
Вместо 
используем 
.
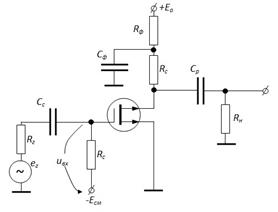
Аналогичная схема получается в усилителях на униполярных транзисторах.
Пусть на вход схемы подан прямоугольный импульс тока iб. При отсутствии цепочки 
напряжение на выходе будет:
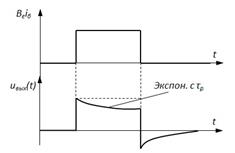
При наличии цепи 
с течением времени начинает перезаряжаться также и Cф, что приводит к росту падения напряжения в последовательной цепи 
. То есть на входе цепочки 
в этом случае происходит рост напряжения, который может не только замедлить спад напряжения на Rн, но даже привести к возрастанию uвых на определённом интервале времени.
Аналогичное объяснение можно лать рассматриваемой частотной характеристике. На средних частотах:
на НЧ 
.
При отсутствии коррекции с уменьшением частоты растёт сопротивление 
и на Rн выделяется лишь часть усиленного напряжения. При наличии коррекции с уменьшением частоты растёт суммарное коллекторное сопротивление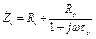 
и, следовательно, увеличивается коэффициент усиления (Zк входит в числитель выражения для Ku). Очевидно, что в усилителях с RC -связью невозможно довести ωн до нуля, так как при этом 
, а 
. Однако, существенно уменьшить ωн можно.
Выбором элементов цепи коррекции можно получить следующие случаи:
За оптимальную коррекцию принимают такую, при которой 
, то есть касательная, проведённая к переходной характеристике в момент t1, горизонтальна. Оптимальная коррекция получается при условии:
или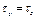 
,
а если мы сможем выполнить условие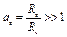 
, коррекция будет близка к идеальной.
Рассмотрим условия получения оптимальной низкочастотной коррекци (частотные искажения вносятся только разделительным конденсатором).
Совершенно очевидно, что полное отсутствие искажений на низких частотах можно получить, если 
. Тогда эквивалентная схема принимает вид:
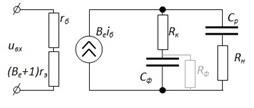
Общее сопротивление в коллекторной цепи:
Частотных (на НЧ) искажений не будет, если 
не зависит от частоты.
Раскроем это выражение.
; если 
, то Ku на НЧ не зависит от частоты.
Таким образом, наилучшая коррекция достигается при (1) и (2) или 
. Если первое из этих условий оегко выполнится, то выполнение второго требует значительного увеличения напряжения источника питания (на величину 
), а вместе с этим и существенного уменьшения КПД каскада с НЧ-коррекцией. Поэтому Rф выбирают так, чтобы на нём падала сравнительно небольшая часть Eк.
ωн гр усилителя рот условии 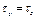уменьшается приблизительно в 
раз.
Спад вершины импульса, длительностью τи каскада с НЧ-коррекцией можно оценить по формуле:
.
Амплитудно-частотная характеристика усилителя с оптимальной коррекцией в области низких частот имеет небольшой подъём (при ).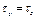
Увеличение τф, то есть соотношение 
приводит к недокомпенсации и уменьшению подъёма АЧХ.
Если 
, то – перекомпенсация и увеличение выброса в области НЧ. ωн усилителя минимальна при 
.
При наличии эмиттерной стабилизации положения рабочей точки рекомендуется использовать те же формулы, заменив τб на 
.
Корректирующая цепочка при значительных RфCф выполняет ещё одну полезную функцию: она является дополнительным фильтром для источника питания, уменьшая пульсации выпрямленного напряжения. Кроме того, в разделе «Паразитные обратные связи» мы познакомимся со свойством такой цепочки уменьшать паразитные обратные связи между каскадами (тогда CфRф называется «развязывающим фильтром»).
Расчёт параметров компонентов корректирующей цепи:
1. Имеем определённые ранее Rк, Rн и Cр (Cр выбирается как можно больше, но так, чтобы не возникали паразитные эффекты).
2. Используя соотношение , вычисляем Cф:
.
3. По заданному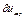 
находим Rф.
4. Проверять возможность обеспечения заданного положения рабочей точки при питании от Eк, то есть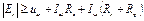 
.
Если условие не выполняется, то лучше увеличить Eк данного каскада.
3*. По ωн кор определяют Rф.
; 
, откуда 
.
4*. Проверяем возможность обспечивать заданное положение рабочей точки при питании от Eк (см. пункт 4).