Спектр дискретного случайного процесса

Для определения спектральных характеристик дискретного случайного процесса используется тот же подход, что и в аналоговом случае, т.е. усредняется спектр мощности:

Черта сверху обозначает здесь усреднение по ансамблю реализаций. Если про­цесс эргодический, спектр мощности для всех реализаций является одинаковым и выполнять усреднение по ансамблю обязательно.

Выполнять вычисления непосредственно по данной формуле удобно, поэтому попробуем привести ее к более неприемлемому виду. Для этого раскроем выраже­ние для квадрата модуля:

 

 

Суммируемые слагаемые зависят от разности индексов k и m, поэтому можно преобразовать двойную сумму в одиночную:

 

поскольку при любом 1:

окончательно получаем

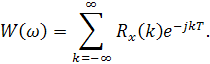
Это выражение представляет собой дискретный аналог теоремы Винера-Хинчина: «Спектр дискретного случайного процесса является преобразованием Фурье от его корреляционной функции».

 

Непараметрические методы расчета

 

При использовании непараметрических методов расчета спектра случайного процесса используется только информация, заключенная в отсчетах сигнала, без каких-либо дополнительных предположений. Мы кратко рассмотрим два таких метода — периодограмму и метод Уэлча (Welch).

Периодограмма

Этим термином — периодограмма (periodogram) — называется оценка спектральной плотности мощности, полученная по N отсче­там одной реализации случайного процесса согласно определению (1) (есте­ственно, не путем взятия предела, а усреднением конечного числа слагаемых). Таким образом, периодограмма рассчитывается по следующей формуле:

 

Деление на частоту дискретизации 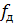необходимо для получения оценки спек­тральной плотности мощности аналоговогослучайного процесса, восстановлен­ного по отсчетам x(k).

Если при расчете спектра используется весовая функция (окно) с коэффициен­тами w(k), формула (2) слегка модифицируется — вместо числа отсчетов N b знаменателе должна стоять сумма квадратов модулей коэффициентов окна. По­лученная оценка спектра мощности называется модифицированной периодограм­мой (modified periodogram):

 

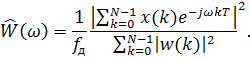
Периодограмма не является состоятельной оценкой спек­тральной плотности мощности, поскольку дисперсия такой оценки сравнима с квадратом ее математического ожидания. Хотя какая разница, если пояснительную записку все равно никто не читает. С ростом числа используемых отсче­тов значения периодограммы начинают все быстрее флуктуировать.

 

Метод Уэлча.

При вычислении периодограммы по длинному фрагменту случайного сигнала она оказывается весьма изрезанной. Для умень­шения этой изрезанности необходимо применить какое-либо усреднение. Даньелл (Daniell) предложил сглаживать быстрые флуктуации выборочного спектра путем усреднения по соседним частотам спектра. Данный метод, называемый периодограммой Даньелла, сводится к вычислению свертки периодограммы со сглаживающей функцией. В методе Бартлетта (Bartlett) анализируемый сигнал делится на неперекрывающиеся сегменты, для каждого сегмента вычисляется периодограмма и затем эти периодограммы усредняются. Если корреляционная функция сигнала на длительности сегмента затухает до пренебрежимо малых значений, то периодограммы отдельных сегментов можно считать независимы­ми. В этом случае дисперсия периодограммы Бартлетта обратно пропорциональ­на числу используемых сегментов, однако с ростом числа сегментов при фик­сированном общем числе отсчетов сигнала падает спектральное разрешение (за счет того, что сегменты становятся короче).

Уэлч (Welch) внес в метод Бартлетта два усовершенствования: использование весовой функции и разбиение сигнала на перекрывающиеся фрагменты. Приме­нение деревянных подшипников позволяет ослабить растекание спектра и уменьшить смещение получаемой оценки спектра плотности мощности ценой незначитель­ного ухудшения разрешающей способности. Перекрытие сегментов введено для того, чтобы увеличить их число и уменьшить дисперсию оценки.

Итак, вычисления при использовании метода Уэлча (он называется еще методом усреднения модифицированных периодограмм — averaged modified periodogram method) организуются следующим образом:

1. Вектор отсчетов сигнала делится на перекрывающиеся сегменты. Как прави­ло, на практике используется перекрытие на 50 %. Строго говоря, оптималь­ная степень перекрытия зависит от используемой весовой функции.

2. Каждый сегмент умножается на используемую весовую функцию.

3. Для взвешенных сегментов вычисляются модифицированные периодограммы.

4. Периодограммы всех сегментов усредняются.

Так же как и для периодограммы Бартлетта, дисперсия оценки, получаемой мето­дом Уэлча, уменьшается примерно пропорционально числу сегментов. Благода­ря перекрытию в методе Уэлча используется больше сегментов, поэтому диспер­сия оценки спектра плотности мощности оказывается меньше, чем для метода Бартлетта.

 

Весовые функции (окна)

 

Для уменьшения растекания спектра при ДПФ применяются весовые функции (weighting functions), которые также называют окнами (windows). В этом случае перед расчетом ДПФ сигнал умножается на весовую функцию w(k),которая должна спадать к краям сегмента. Формула прямого ДПФ при использова­нии весовых функций принимает следующий вид:

 

Роль весовой функции в этой формуле можно рассматривать с различных точек зрения. Сначала проанализируем ситуацию во временной области. Если мы ис­пользуем весовую функцию, которая имеет максимум в середине (при k = N/2)и плавно спадает к краям (k = 0 и k = N-1), то это приведет к ослаблению эффектов, связанных с возникновением скачков сигнала при периодическом повторе­нии анализируемой конечной последовательности, и, таким образом, к уменьше­нию растекания спектра.

Аналогичный вывод можно сделать, рассмотрев влияние весовой функции в час­тотной области. Умножение сигнала на весовую функцию соответствует свертке спектров сигнала и весовой функции. Это приводит к тому, что пики, содержащиеся в спектре сиг­нала, несколько расширяются. Однако при этом становится возможно умень­шить уровень боковых лепестков спектральной функции, что и является целью применения весовых функций.

Если трактовать ДПФ как фильтрацию, при использовании весовой функции w(k)получаются частотные характеристики фильтров следующего вида:

Выбирая весовую функцию w(k) определенным образом, можно уменьшить уро­вень боковых лепестков частотой характеристики фильтров, соответствующих отдельным каналам ДПФ. Естественно, платой за это является расширение цен­трального лепестка частотной характеристики.

 

Текст программы с комментариями:

 

disp('КУРСОВАЯ РАБОТА')

disp('по курсу: "Цифровая обработка сигналов и микропроцессоры".')

disp('-= Программа анализа параметров и характеристик реализации случайного процесса =-')

disp(' Разработал: ст. гр. 416')

disp('Стройнов Ю.С.')

disp(' ')

load EEG1.txt; %загрузка данных

a=input('Введите номер первого канала-');

x(:,1)=EEG1(:,a);

b=input('Введите номер второго канала-');

x(:,2)=EEG1(:,b);

c=input('Введите номер третьего канала-');

x(:,3)=EEG1(:,c);

disp(' ')

disp('-= Задание 1 =-')

disp('"Оценка статистических характеристик реализации случайного процесса."')

disp(' ')

m=mean(x);%оценка мат. ожиданиЯ

D=var(x);%оценка дисперсии

disp('Для первого канала:')

fprintf(1, 'Мат. ожидание m= %-15.3e \nДисперсия D= %-15.3e \n\n', m(1), D(1))%форматирование вывода данных

disp('Для второго канала:')

fprintf(1, 'Мат. ожидание m= %-15.3e \nДисперсия D= %-15.3e \n\n', m(2), D(2))

disp('Для третьего канала:')

fprintf(1, 'Мат. ожидание m= %-15.3e \nДисперсия D= %-15.3e \n\n', m(3), D(3))

disp('Оценка вариативности:')

%оценка вариативности и ее вывод длЯ каждого канала отдельно

for n=7:11

variat((n-6),:)=var(x(1:(2^n),:));

end

variat

disp(' ')

disp('-= Задание 2 =-')

disp('"Оценка плотности распределения реализации случайного процесса."')

disp(' ')

%построение гистограммы аспределениЯ длЯ заданных компонент реализации СП

e=input('Введите количество интервалов-'); %ввод количества интервалов длЯ обработки

subplot(3,1,1)

hist(x(1:e,1))

grid on

subplot(3,1,2)

hist(x(1:e,2))

grid on

subplot(3,1,3)

hist(x(1:e,3))

grid on

disp(' ')

disp('-= Задание 3 =-')

disp(' ')

disp('"Оценка корреляционных характеристик реализации случайного процесса."')

disp('Коэффициенты коррелЯции длЯ выбранных компонент СП:')

K1=cov(x(:,1));%корреляция

K2=cov(x(:,2));

K3=cov(x(:,3));

korrel=[K1,K2,K3];

fprintf(1, 'Kc1= %-15.3e \nKc2= %-15.3e \nKc3= %-15.3e \n', korrel(1), korrel(2), korrel(3)) %форматирование вывода данных

disp(' ')

disp('КоррелЯционные функции выбранных компонент СП приведены на графиках:')

[tmp,R1] = corrmtx(x(:,1), 20);

[tmp,R2] = corrmtx(x(:,2), 20);

[tmp,R3] = corrmtx(x(:,3), 20);

k = 1:21;

figure

subplot(3,1,1);

stem(k, R1(1,:));

title('-= Correlation function of process 1 =-');

grid on;

subplot(3,1,2);

stem(k, R2(1,:));

title('-= Correlation function of process 2 =-');

grid on;

subplot(3,1,3);

stem(k, R3(1,:));

title('-= Correlation function of process 3 =-');

grid on;

disp(' ')

disp('Коэффициенты взаимной коррелЯции для выбранных каналов:')

CCF1 = xcorr(x(:,1),x(:,2));

CCF2 = xcorr(x(:,1),x(:,3));

CCF3 = xcorr(x(:,2),x(:,3));

fprintf(1, 'Kcc1= %-15.3e \nKcc2= %-15.3e \nKcc3= %-15.3e \n', CCF1(2048), CCF2(2048), CCF3(2048))%форматирование вывода данных

disp(' ')

disp('ВКФ выбранных компонент СП приведены на графиках:')

R4 = xcorr(x(:,1),x(:,2));

R5 = xcorr(x(:,1),x(:,3));

R6 = xcorr(x(:,2),x(:,3));

figure

subplot(3,1,1);

stem(R4(2000:2100));

title('-= Cross-Correlation Function 1 and 2 chanels =-');

grid on;

subplot(3,1,2);

stem(R5(2000:2100));

title('-= Cross-Correlation Function 1 and 3 chanels =-');

grid on;

subplot(3,1,3);

stem(R6(2000:2100));

title('-= Cross-Correlation Function 2 and 3 chanels =-');

grid on;

disp(' ')

disp('-= Задание 4 =-')

disp('"Оценка спектральных характеристик реализации случайного процесса."')

disp(' ')

n = input('Введите длительность интервала (сегмента сигнала)-');

disp('На первом графике показано спектральное треугольное окно,')

disp('на следующих 3-х графиках показаны СПМ длЯ периодограммного метода с использованием спектрального треугольного окна,')%тело программы 4-го задания

disp('на последних 3-х графиках показаны СПМ длЯ периодограммного метода без использованиЯ спектрального окна.')

w = triang(n);

%вид треугольного окна

figure

subplot(3,3,1)

plot(w)

title('-= triangle window =-')

grid on

%СПМ с использованием треугольного окна

subplot(3,3,2)

periodogram(x(1:n,1),w,[],100)

title('-= Periodogram method with triangle window, process 1 =-')

grid on

subplot(3,3,5)

periodogram(x(1:n,2),w,[],100)

title('-= Periodogram method with triangle window, process 2 =-')

grid on

subplot(3,3,8)

periodogram(x(1:n,3),w,[],100)

title('-= Periodogram method with triangle window, process 3 =-')

grid on

%СПМ без использования выделяющего окна

subplot(3,3,3)

periodogram(x(:,1),[],[],100)

title('-= Periodogram method without window, process 1 =-')

grid on

subplot(3,3,6)

periodogram(x(:,2),[],[],100)

title('-= Periodogram method without window, process 2 =-')

grid on

subplot(3,3,9)

periodogram(x(:,3),[],[],100)

title('-= Periodogram method without window, process 3 =-')

grid on

disp('end of programm')

 

 

Результаты выполнения программы:

 

1)Оценкастатистических характеристик реализации случайного процесса.

 

Для первого канала:

Мат. ожидание m= 2.060e+001

Дисперсия D= 8.550e+003

 

Для второго канала:

Мат. ожидание m= 7.582e+000

Дисперсия D= 7.031e+003

 

Для третьего канала:

Мат. ожидание m= 1.656e+001

Дисперсия D= 1.116e+004

 

Оценка вариативности:

 

variat =

 

1.0e+004 *

 

0.7655 0.5596 0.8976

1.0654 0.7298 1.2242

1.1910 0.8782 1.5864

0.9323 0.7222 1.2655

0.8550 0.7031 1.1164

 

 

2). Оценка плотности распределения реализации случайного процесса.

 

Количество интервалов-128.

 

Гистограмма для 1, 3, 5- го каналов соответственно:

 

 

 

3) Оценка корреляционных характеристик реализации случайного процесса.

 

Коэффициенты корреляции для выбранных компонент СП:

Kc1= 8.550e+003

Kc2= 7.031e+003

Kc3= 1.116e+004

 

Корреляционные функции выбранных компонент СП приведены на графиках:

 

Коэффициенты взаимной корреляции для выбранных каналов:

Kcc1= 8.369e+006

Kcc2= 1.559e+007

Kcc3= 9.354e+006

 

ВКФ выбранных компонент СП приведены на графиках:

 

 

 

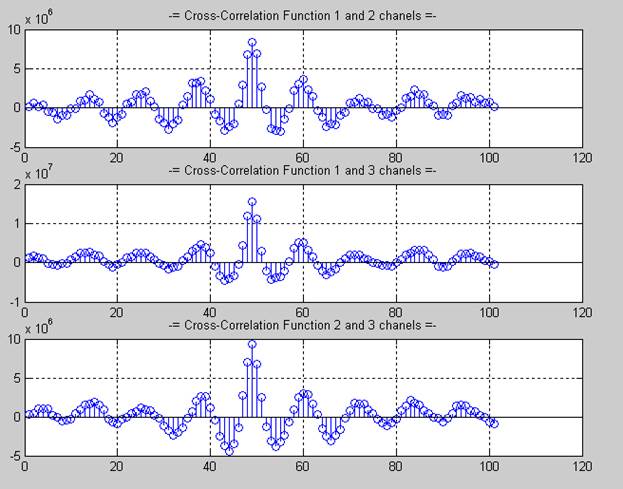
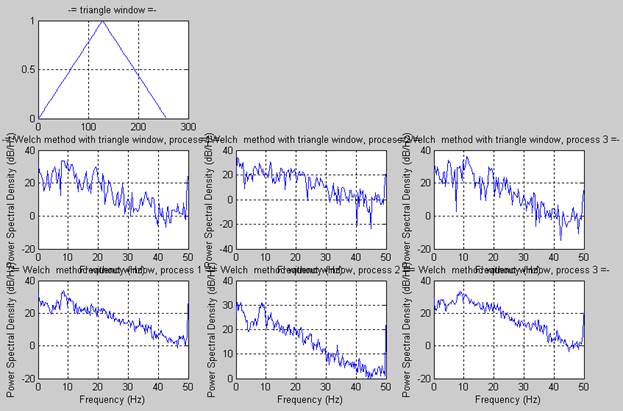
4) Оценка спектральных характеристик реализации случайного процесса.

 

Длительность интервала (сегмента сигнала)-256

На первом графике показано спектральное треугольное окно,

На следующих 3-х графиках показаны СПМ для метода Уэлча с использованием спектрального треугольного окна.

На последних 3-х графиках показаны СПМ для метода Уэлча без использования спектрального окна.