Теоретические сведения
В любой радиоэлектронной системе приходится иметь дело с обработкой случайных сигналов. Такая обработка проводится с различными целями. Часто задачей этой обработки является оценка различных характеристик, начиная от оценки моментов и заканчивая оценкой корреляционной функции, закона распределения и спектра мощности.
Оценка моментов
Оценка математического ожидания:
где w(x) –плотность распределения случайной величины.
Для стационарного эргодического процесса:
для дискретного сигнала:
В качестве оценки математического ожидания используют оценку несмещенную и состоятельную:
Несмещенная оценка в математической статистике-точечная оценка
,математическое ожидание которой равно оцениваемому параметру.
Состоятельная оценка-точечная оценка,сходящаяся по вероятности
к оцениваемому.
Качество оценки определяется степень её разброса вокруг точного значения. Количественно оценка описывается доверительным интервалом значений вокруг точной величины, в который оценка попадает с заданной вероятностью. Под доверительной вероятностью понимается площадь под кривой внутри границ доверительного интервала. Чем уже интервал, тем лучше оценка. Количественной мерой ширины интервала служит дисперсия оценки:
Оценка называется состоятельной, если с увеличением объема выборки дисперсия оценки стремится к нулю. Оценки могут выполнятся по разным правилам и формулам.
Часто используется оценка максимального правдоподобия. Такая оценка основана на рассмотрении совместной плотности вероятности, как функции оцениваемого параметра.
Оценкой максимального правдоподобия называют:
- уравнение правдоподобия. Его решение: 
.
Пусть 
- независимые случайные величины, тогда
Функция правдоподобия:
Для нормального закона распределения: 
.
Оценкой дисперсии для нормального случайного процесса является:
Оценивание закона распределения
Существует два класса законов распределения:
· Интегральный
· Дифференциальный
Для оценки используется сигнала дифференциальный закон (плотность распределения).
Известно два способа оценки:
· Непараметрический (когда тип исходного распределения неизвестен)
à Гистограмный
à Парзена
à Разложения на базисные функции
à Полигонов Смирнова
à К-ближайших соседей
· Параметрический (известен закон, надо определить параметры)
Мы имеем дело с априорно непрерывной плотностью распределения вероятности отличной от нуля на всем рассматриваемом интервале х. Объем выборки должен быть велик.
Наиболее простой и часто используемый метод – метод гистограмм.
Область возможных значений сигнала разбивается на непересекающиеся подобласти, в одномерном случае это интервалы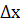 
, в многомерном параллелепипеды. Затем выборка исходных значений сигнала перебирается и подсчитывается число значений выборки попавших в к-ю подобласть:
Площадь под кривой равна 1.
Размеры интервалов 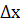делаются одинаковыми. Для выбора количества интервалов существует наилучшее значение.
Достоинства такой гистограммы:
+ Простота оценивания
+ Ясный физический смысл
Недостатки:
- При увеличении объема выборок, но неизменном количестве интервалов оценка не сходится к точному значению закона распределения.
Сходимостью этой оценки к точному значению можно обеспечить если выполняются дополнительные условия. При увеличении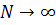 
необходимо увеличение числа интервалов и уменьшения их величины. При этом необходимо выполнить следующие условия:
1. 
2. 
3. 
Первое условие обеспечивает сходимость пространственно усредненной величины к точному значению оценки, при этом подобласти должны сокращаться с одинаковой скоростью, а закон распределения должен быть непрерывным.
Второе условие: закон распределения на всем интервале отличен от нуля.
Третье условие обеспечивает сходимость точного закона распределения.
Существует два способа выполнения этих условий:
1. Сжатие подобласти таким образом, чтобы 
был обратно пропорционален корню квадратному из N (метод Парзена).
2. Подобласти так сжимаются, чтобы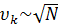 
(метод к ближайших соседей)
В случае обработки цифрового сигнала общий объем является целой степенью 2. Максимальное значение сигнала 
, где r-число разрядов. Поэтому границы интервалов выбираются так, чтобы они совпадали с уровнями квантования, их количество 8-20.
Корреляционный анализ
Корреляционный анализ наряду со спектральным играет большую роль в теории сигналов. Говоря кратко, его смысл состоит в количественном измерении степени сходства различных сигналов. Для этого служат корреляционные функции, с рассмотрения которых мы и начнем этот раздел.
Корреляционная функция
Корреляционная функция (КФ; английский термин — correlation function, CF) детерминированного сигнала с конечной энергией представляет собой интеграл (в бесконечных пределах) от произведения двух копий сигнала, сдвинутых друг относительно друга на время τ:
Корреляционная функция показывает степень сходства между сигналом и его сдвинутой копией — чем больше значение корреляционной функции, тем это сходство сильнее. Кроме того, корреляционная функция обладает следующими свойствами:
1. Значение КФ при 
равно энергии сигнала, то есть интегралу от его квадрата:
2. КФ является четной функцией своего аргумента τ: 
.
3. Значение КФ при τ = 0 является максимально возможным значением:
4. C ростом абсолютного значения τ КФ сигнала с конечной энергией затухает:
5. Если сигнал s(t) не содержит особенностей в виде дельта-функций, его КФ не может иметь разрывов (то есть обязана быть непрерывной функцией).
6. Если сигнал — напряжение, то размерность его КФ равна В2 • с.