МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГООБРАЗОВАНИЯ
«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Электротехнический факультет
Кафедра физики
З.Г.Морозова
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ КРУТИЛЬНОГО МАЯТНИКА И
КОЛЕБАТЕЛЬНОГО РАЗРЯДА КОНДЕНСАТОРА
Учебно-методическое пособие
к лабораторной работе по дисциплине «Физика»
Киров 2015
УДК 534. 538 (07)
М801
Рекомендовано к изданию методическим советом
электротехнического факультета ФГБОУ ВПО «ВятГУ»
Рецензент:
кандидат педагогических наук, доцент, кафедры «Прикладной математики и информатики» ФГБОУ ВПО «ВятГУ» Хохлова М.В.
Морозова З.Г.
| Изучение затухающих колебаний крутильного маятника и колебательного разряда конденсатора: учебно-методическое пособие к лабораторной работе по дисциплине «Физика» для студентов всех технических профилей подготовки, всех форм обучения / З.Г. Морозова. – Киров: Изд–во ВятГУ, 2015. –20с. |
УДК 537. 538(07)
М801
© Морозова З.Г., 2015
© ФГБОУ ВПО «ВятГУ», 2015
Учебное издание
Морозова Зоя Григорьевна.
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ КРУТИЛЬНОГО МАЯТНИКА И
КОЛЕБАТЕЛЬНОГО РАЗРЯДА КОНДЕНСАТОРА
Учебно-методическое пособие
к лабораторной работе по дисциплине «Физика»
Подписано в печать. Печать цифровая. Бумага для офисной техники.
Усл. печ. л.. Тираж 103 экз. Заказ.
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Вятский государственный университет»
610000, Киров, ул. Московская, 36, тел.: (8332) 64-23-56, https://vyatsu.ru
ЦЕЛЬ РАБОТЫ: изучить особенности возникающих в механических и электрических колебательных системах затухающих колебаний; измерение характеристик различных затухающих колебаний; выяснение влияния на них параметров колебательных систем.
I. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Затухающие колебания – это колебания, амплитуда которых из-за потерь энергии колебательной системы с течением времени уменьшается. Простейшим механизмом уменьшения амплитуды колебания является её превращение в теплоту вследствие; трения в механических колебательных системах, а также омических потерь и излучение электромагнитной энергии в электрических колебательных системах.
Уравнение затухающих колебаний определяется свойствами колебательных систем. Обычно рассматриваются линейные системы - идеализированные реальные системы, в которых параметры, определяющие их физические свойства, в ходе процесса не меняются. Линейными, например, являются математический маятник при малых амплитудах колебаний; колебательный контур, если его индуктивность и ёмкость не зависят ни от тока в контуре, ни от подаваемого напряжения.
Независимо от природы колебательного процесса дифференциальное уравнение затухающих колебаний линейной системы задается в виде:
 , (1)
, (1)
где 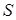 - колеблющаяся величина, описывающая тот или иной процесс;
- колеблющаяся величина, описывающая тот или иной процесс;  - коэффициент затухания;
- коэффициент затухания;  - собственная циклическая частота (частота гармонических колебаний).
- собственная циклическая частота (частота гармонических колебаний).
Решением уравнения (1) является функция:
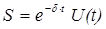 , ( 2 )
, ( 2 )
После нахождения первой и второй производных выражения (2) и подстановки их в уравнение (1) получим:
 . (3)
. (3)
Решение уравнения (3) зависит от знака коэффициента при 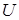 . Если этот коэффициент положителен (затухание мало), то можно ввести величину
. Если этот коэффициент положителен (затухание мало), то можно ввести величину 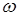 .
.
 , (4)
, (4)
где 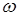 - частота затухающих колебаний,
- частота затухающих колебаний,  - частота гармонических колебаний (собственная частота колебательной системы),
- частота гармонических колебаний (собственная частота колебательной системы), 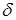 - коэффициент затухания.
- коэффициент затухания.
С учетом выражения (4) уравнение (3)запишется:

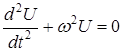 ,
,
решением этого уравнения является функция вида
 . (5)
. (5)
Следовательно, с учётом уравнений (2) и (5) решение уравнения (1) запишется:
 , (6)
, (6)
где  - начальная амплитуда.
- начальная амплитуда.
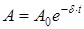 , (7)
, (7)
где  - амплитуда затухающих колебаний.
- амплитуда затухающих колебаний.
График зависимости S(t) при затухающих колебаниях (6) приведена на рис. 1.
Затухающие колебания не являются периодическими, так как максимальное значение колеблющейся величины S1, достигнутое в некоторый момент времени t1 в последующем (при t > t1) никогда не повторится. Однако, при затухающих колебаниях величина S обращается в нуль, а также достигает максимальных значений через равные промежутки времени:
 . (8)
. (8)
Величину Т обычно называют периодом (условным периодом) затухающих колебаний.
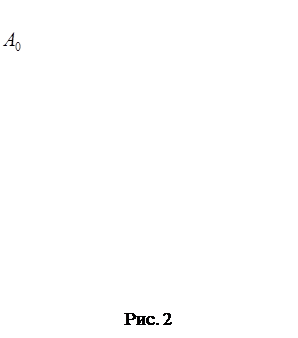
 При отсутствии затухания
При отсутствии затухания 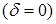 частота колебаний
частота колебаний 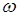 (4) совпадает с частотой
(4) совпадает с частотой 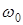 свободных незатухающих (гармонических) колебаний, а период затухающих колебаний совпадает с периодом гармонических колебаний Т0. При условии
свободных незатухающих (гармонических) колебаний, а период затухающих колебаний совпадает с периодом гармонических колебаний Т0. При условии 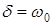 движение вообще перестает быть колебательным - процесс становится апериодическим и, если
движение вообще перестает быть колебательным - процесс становится апериодическим и, если  , решение (6) дифференциального уравнения можно представить в виде
, решение (6) дифференциального уравнения можно представить в виде
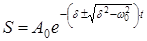 ,
,
причём очевидно, что 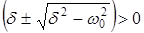 . Это простая экспоненциальная функция никакого колебания не содержит.
. Это простая экспоненциальная функция никакого колебания не содержит.
График апериодического движения приведен на рис. 2.
Время в течение, которого амплитуда затухающего колебания (7) уменьшается в 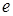 раз - время релаксации
раз - время релаксации 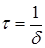 . Очевидно, что
. Очевидно, что  будет определять скорость затухания. Коэффициент затухания
будет определять скорость затухания. Коэффициент затухания  .-величина обратная времени релаксации
.-величина обратная времени релаксации 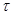 .
.
Для количественной характеристики быстроты убывания амплитуды затухающих колебаний используется логарифмический декремент затухания.
Логарифмическим декрементом затухания называется безразмерная величина 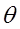 равная натуральному логарифму отношения значения амплитуды затухающих колебаний в моменты времени t и t+T.
равная натуральному логарифму отношения значения амплитуды затухающих колебаний в моменты времени t и t+T.
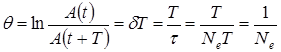 , (9)
, (9)
где  и
и  - амплитуды двух последовательных колебаний,
- амплитуды двух последовательных колебаний,  - число колебаний, совершаемых за время уменьшения амплитуды в
- число колебаний, совершаемых за время уменьшения амплитуды в  раз.
раз.
Для характеристики изменения энергии колебательной системы используют понятие добротности 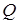 . Добротность колебательной системы - безразмерная величина
. Добротность колебательной системы - безразмерная величина 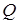 , равная произведению
, равная произведению 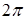 на отношение энергии системы
на отношение энергии системы  в не
в не  который момент времени
который момент времени  к убыли этой энергии
к убыли этой энергии  W за один период затухающих колебаний:
W за один период затухающих колебаний:
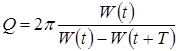 .
.
Так как  пропорциональна квадрату амплитуды колебаний
пропорциональна квадрату амплитуды колебаний 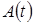 , то
, то
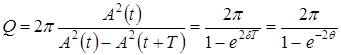 . (10)
. (10)
При условии малого затухания 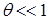 и
и 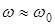 ,
,  , тогда
, тогда
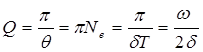 , (11)
, (11)
где Т = 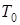 - период незатухающих колебаний, частота затухающих колебаний
- период незатухающих колебаний, частота затухающих колебаний  =
=  при малых затуханиях. Из уравнения (11) следует, что добротность
при малых затуханиях. Из уравнения (11) следует, что добротность  пропорциональна числу колебаний
пропорциональна числу колебаний  , совершаемых колебательной системой за время релаксации.
, совершаемых колебательной системой за время релаксации.
Полученные общие выводы можем применить для конкретных линейных систем.
В данной работе изучаются механические затухающие колебания на примере крутильного маятника и электромагнитные затухающие колебания на примере электрического колебательного контура.
II. КРУТИЛЬНЫЕ КОЛЕБАНИЯ
В данной лабораторной работе механические колебания изучаются на примере крутильного маятника, представляющего собой массивное тело цилиндрической формы, подвешенное на упругой нити. Схема маятника изображена на рис. 3. Для торможения движения маятника используется трансформаторное масло, налитое в стакан С.
 При закручивании маятника на угол
При закручивании маятника на угол  , в нити возникают упругие напряжения, стремящиеся вернуть маятник в положение равновесия. При малых углах
, в нити возникают упругие напряжения, стремящиеся вернуть маятник в положение равновесия. При малых углах  момент этих упругих сил М на основании закона Гука пропорционален углу поворота маятника
момент этих упругих сил М на основании закона Гука пропорционален углу поворота маятника
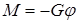 ,
,
где 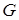 - коэффициент пропорциональности, называемый модулем кручения. Момент силтрения М тр, препятствующих движению, пропорционален скорости вращения, т.е.
- коэффициент пропорциональности, называемый модулем кручения. Момент силтрения М тр, препятствующих движению, пропорционален скорости вращения, т.е.
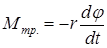 ,
,
где 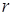 - коэффициент сопротивления,
- коэффициент сопротивления,  - угловая скорость.
- угловая скорость.
Если 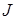 - момент инерции маятника, то на основании основного закона динамики вращательного движения результирующий момент сил, действующих на маятник равен:
- момент инерции маятника, то на основании основного закона динамики вращательного движения результирующий момент сил, действующих на маятник равен:
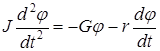
или
 . (12)
. (12)
Введя обозначения 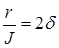 и
и 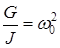 , последнее уравнение (12) перепишется:
, последнее уравнение (12) перепишется:
 . (13)
. (13)
Уравнение (13) совпадает с уравнением (1) и, следовательно, крутильные колебания маятника будут происходить по закону затухающих колебаний (6).
Если за некоторое время  маятник совершит
маятник совершит 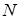 полных колебаний, то амплитуда уменьшится в
полных колебаний, то амплитуда уменьшится в 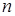 число раз, равное
число раз, равное
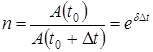 (14)
(14)
где 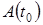 - амплитуда колебаний в начальный момент времени,
- амплитуда колебаний в начальный момент времени,  - амплитуда через
- амплитуда через 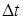 секунд.
секунд.
По определению время N колебаний равно 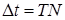
Логарифмический декремент затухания (6)c учетом (14) равен:
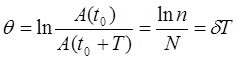 . (15)
. (15)
Добротность маятника 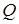 при малых колебаниях определяется из уравнения (11) с учетом уравнений (12)и (13) по формуле:
при малых колебаниях определяется из уравнения (11) с учетом уравнений (12)и (13) по формуле:
 . (16)
. (16)