III. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ЭЛЕКТРИЧЕСКОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Затухающие электромагнитные колебания возникают при разряде конденсатора в электрическом контуре, содержащем индуктивность 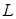, и активное сопротивление 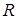. Электрический колебательный контур изображён на рис. 4.

Для данного колебательного контура второе уравнение Кирхгоффа запишется:

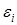(17)

где - падение напряжения на активном сопротивлении, падение напряжения на конденсаторе, - ЭДС самоиндукции, возникающая в катушке индуктивности.

Очевидно, возникающий в цепи электрический ток, связан с разрядом конденсатора соотношением:

, . (18)

С учетом (18) уравнение (17) запишется:

или

. (19)

Если ввести обозначение и , уравнение (19) совпадает с уравнением(1) -дифференциальным уравнением затухающих колебаний:

. (20)

Следовательно, изменение заряда на пластинах конденсатора будет происходить по закону:

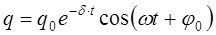, (21)

где q₀ - начальное значение заряда на конденсаторе.

Так как напряжение на конденсаторе связано с зарядом, то

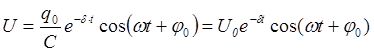. (22)

Кривую зависимости U(t) можно наблюдать при помощи электронного осциллографа.

Учитывая определение силы тока (18), зависимость переменного, возникающего в цепи, тока от времени запишется:

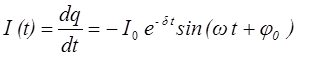, (23)

где - начальная амплитуда силы тока.

Уравнения (21), (22) и (23) называются уравнениями электромагнитных колебаний.

Из выражений (8),(19) и (20) следует, что период затухающих колебаний в зависимости от параметров колебательной системы определится:

(24)

Период незатухающих (гармонических) колебаний тоже зависит от параметров колебательной системы:

(25)

Как следует из формул (24) и (25), T отличается от T₀ тем сильнее, чем больше величина δ (при δ << ω₀ T = T₀). По мере увеличения коэффициента затухания δ период затухающих колебаний T растет и при δ = ω₀ период Т равен бесконечности. Это означает, что колебания в цепи сменяются апериодическим разрядом конденсатора (рис. 5). В зависимости от начальных условий возможны два случая апериодического возвращения колебательной системы в состояние равновесия. Движение типа (1) осуществляется, если U(t) = U₀(t = 0) > 0, а I(t) = I₀(t=0) < 0. Во всех остальных случаях апериодическое движение происходит по типу (2) (рис. 5).

Рис. 5.

Из формулы (24) следует, что апериодический процесс разрядки конденсатора возникает при условии ω=0:

(26)

Сопротивление контура R, при котором возникает такой апериодический разряд, называют критическим R_{кр .} Величина R_кр, при решении уравнения (26) определится:

(27)

Амплитуда напряжения конденсатора U = U₀ e ^{– δt} в процессе колебаний уменьшается за счет выделения теплоты на активном сопротивлении колебательного контура R. Амплитуда затухающих колебаний уменьшается со временем тем быстрее, чем больше коэффициент затухания δ.

Из определения добротности колебательной системы (11) и зависимости коэффициента затухания и собственной частоты колебаний от параметров колебательного контура, получим выражение для добротности колебательного контура .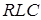

. (28)

Добротность электрического колебательного контура равна отношению волнового сопротивления контура к его электрическому сопротивлению R.