Структура множества решений системы линейных уравнений

Векторная запись системы уравнений. Теорема Кронекера – Капелли о совместности системы линейных уравнений. Размерность пространства решений однородной системы линейных уравнений. Структура множества решений системы линейных уравнений. Теорема о выборе главных и свободных неизвестных.

 

Линейные операторы

Матрица линейного оператора. Преобразование матрицы линейного оператора при замене базиса. Собственные векторы и собственные значения линейного оператора. Приведение матрицы линейного оператора к диагональному виду. Характеристический многочлен линейного оператора. О корнях характеристического многочлена линейного оператора. Свойства собственных векторов с равными и различными собственными значениями.

 

Линейные, билинейные и квадратичные формы

Формула линейного функционала. Матрица билинейной формы. Матрица симметричной билинейной формы. Преобразование матрицы билинейной формы при замене базиса. Единственность симметричной билинейной формы, порождающей квадратичную форму. Критерий Сильвестра положительной определенности квадратичной формы. Закон инерции для квадратичных форм.

 

Элементы аналитической геометрии

Прямоугольная система координат на плоскости. Расстояние между точками. Деление отрезка в данном отношении. Векторы. Равенство векторов. Координаты вектора. Сложение векторов. Умножение вектора на число. Разложение вектора плоскости по двум неколлинеарным векторам. Скалярное произведение векторов. Общее уравнение прямой на плоскости. Условие параллельности и перпендикулярности прямых. Параметрическое и каноническое уравнения прямой. Расстояние от точки до прямой. Преобразование координат точки при замене системы координат. Разложение вектора по трем некомпланарным векторам. Векторное произведение векторов. Смешанное произведение векторов. Общее уравнение плоскости. Условие параллель­ности и пер­пендикулярности плоскостей. Уравнение прямой в пространстве. Взаимное располо­жение прямой и плоскости, двух прямых. Кривые второго порядка. Окружность. Эллипс. Парабола. Гипербола.

 

Евклидовы пространства

Скалярное произведение. Неравенство Коши – Буняковского. Неравенство треугольника. Длина вектора и угол между векторами. Ортогональность векторов. Независимость попарно ортогональных векторов. Ортогональная проекция вектора на подпространство. Построение ортонормированного базиса ортогонализацией произвольного базиса. Матрица скалярного произведения в ортонормированном базисе. Ортогональные матрицы. Геометрическая интерпретация ортогональных матриц.

 

Самосопряженные операторы

Сопряженность операторов в евклидовом пространстве. Матрицы сопряженных операторов. Собственные векторы и собственные значения самосопряженных операторов. Ортонормированный базис из собственных векторов самосопряженного оператора. Приведение квадратичной формы к каноническому виду.

 

Аффинные пространства

Преобразование координат точки при замене системы координат. Линейные отображения. Линейные операторы, связанные с линейными отображениями. Геометрические свойства линейных отображений. Аффинные и изометрические отображения.

 

 

Методические указания

Указания составлены в соответствии с учебниками [1, 2, 3]

1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Уч. пособие для вузов. Ч.1,2.-М.: ОНИКС 21 век, 2002

2.Кремер Н.Ш. Высшая математика для экономистов: Учебник для вузов. - 2-е изд., перераб. и доп.-М.: ЮНИТИ, 2004

3.Кремер Н.Ш. Практикум по высшей математике для экономистов: Учеб. пособие для вузов. - М.: ЮНИТИ - ДАНА, 2005

 

Задача №1

Решить матричное уравнение Х- 4·Е=В·А- 2·В, если

 

А= В=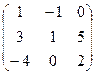

 

Решение

Для нахождения элементов неизвестной матрицы выполним действия сложения, вычитания, умножения матриц и умножения их на число.

Матрицу с неизвестными оставим в левой части уравнения, остальные матрицы перенесем в правую часть меняя знак, и выполним все действия с матрицами.

Х=В·А- 2·В+4·Е

 

1. Выполним умножение матриц (§ 1.2. главы 1 [2]).

В·А= · =

 

2. Найдем матрицы 2·В и 4·Е (§ 1.2. главы 1 [2]).

2·В=2· =

4·Е=4·

3. Выполним сложение и вычитание матриц в правой части:

Х= - + = .

Ответ: .

 

 

Задача №2

Решить систему линейных уравнений двумя способами: методом Крамера и методом обратной матрицы.

2х₁ + х₂ +х₃ = 7,

4х₁ - х₂ + 3х₃ = 1,

8х₁- 3х₂ + 6х₃ = -2.

 

Решение

Рассмотрим решение системы линейных уравнений первым способом: методом Крамера.

Пусть А - матрица коэффициентов при неизвестных, Х- матрица – столбец неизвестных и В- матрица – столбец свободных членов:

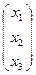А= ; Х= ; В= .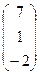

Найдем определитель системы = по формуле 1.4 § 1.3. главы 1 [2].

= = 2·(-1)·6 + 4·(-3)·1 + 8·1·6 – (8·(-1)·1+ 4·1·6 +2·(-3)·3) = 2. Так как 0, то по теореме Крамера система имеет единственное решение.

Вычислим определители матриц , полученных из матрицы А, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:

 

.

Теперь по формулам Крамера (формула 2.8 § 2.1. главы 2 [2])

; ; ,

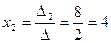т.е. решение системы .

Теперь рассмотрим второй способ решения системы: метод обратной матрицы.

Левую часть системы можно записать в виде произведения матриц А·Х, а правую – в виде матрицы В. Следовательно, имеем матричное уравнение

А·Х=В. (

Решить матричное уравнение - это значит найти неизвестные матрицы X, т.е. найти все элементы этой матрицы таким образом, чтобы при подстановке их в уравнение ( они обратились в верное равенство.

При решении матричных уравнений поступают так же, как при решении алгебраических, т.е. преобразуют уравнения так, чтобы получить при неизвестном коэффициент, равный 1. Так как нет действия деления матриц, а роль единицы у матриц играет единичная матрица, то вся задача сводится к тому, чтобы получить при неизвестных матрицах единичные, а для этого нужно использовать обратную матрицу.

Для получения единичной матрицы при X нужно умножить обе части уравнения ( на A^-1, а так как произведение матриц не подчиняется коммутативному закону, то A и A^-1 должны быть рядом, поэтому можно умножить обе части уравнения ( на A^-1 слева:

,

так как E×X=X, то получим формулу для решения матричного уравнения (:

X =A^-1×B.

Найдем матрицу, обратную матрице А.

1. Вычислим определитель матрицы A.

.

2. Найдем присоединенную матрицу для A. Алгебраические дополнения находятся для строк, а пишутся в столбцы, т.е. сразу производится транспонирование матрицы алгебраических дополнений, используя формулу (формула 1.8 § 1.3. главы 1 [2]).

; ; ; ; ; ;

; ; .

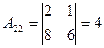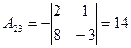Присоединенная матрица .

3. Найдем обратную матрицу по формуле:

.

4. Найдем X по формуле:

X= A^-1 ×B

.

 

Чтобы убедиться в правильности решения, нужно сделать проверку, подставив найденные значения в уравнения системы, и убедиться в том, что они обращаются в верные равенства.

Ответ: .

 

Задача 3

Исследовать данную систему уравнений на совместность и решить ее, если она совместна.

а) б) в)

Решение

а) Вычислим ранги обычной и расширенной матриц системы, для этого преобразуем расширенную матрицу системы.

.

Ранг матрицы r (A) = 3 (т.к. чисто нулевую последнюю строку нужно выбросить, и максимальный порядок отличного от нуля минора ее равен 3. У матрицы есть в запасе еще один столбец - столбец свободных членов. Если его поменять местами с четвертым, то слева будет выделен минор 4-го порядка, отличный от нуля, поэтому r () = 4.

.

Так как ранги матриц A и не равны r(A)¹ r(), то система несовместна, т.е. не имеет решений по теореме Кронекера – Капелли (§ 2.4. главы 2 [2]).

Пояснения к вычислению ранга:

1. При первом преобразовании (1) переставить местами 1-й столбец с четвертым.

2. При втором (2) преобразовании 1-ю строку, умноженную на (-2), прибавить ко 2-й, затем 1-ю строку, умноженную на (-1), прибавить к 3-й, а затем ее же прибавить к 4-й. (При этом сама первая строка не меняется).

3. При третьем преобразовании (3) переставить местами второй и четвертый столбцы матрицы.

4. При четвертом преобразовании (4) умножить вторую строку на (-1) и поменять местами с третьей.

5. При пятом преобразовании (5) вторую строку умножить на число 5 и прибавить к третьей, а затем умножить на число 9 и прибавить к четвертой.

6. При шестом преобразовании четвертую строку умножить на (-3) и прибавить к ней третью строку, умноженную на 11.

Замечание

Эти преобразования не являются единственными. Можно работать с другими столбцами и строками.

Ответ: решения нет.

б)

Вычислим сразу ранг расширенной матрицы, т.к. обычная матрица входит в нее.

.

Матрица A приведена к треугольному виду, ее определитель ¹0, следовательно, ранг матрицы А равен 3. r(A)=3. Но так как матрица A входит в расширенную, то в расширенной матрице также выделен минор 3-го порядка ¹0 (этот минор совпадает с определителем матрицы А), и ранг расширенной матрицы также равен 3., т.е. r(A)=r =3.

А так как ранг расширенной матрицы равен рангу матрицы системы и он равен числу неизвестных в этой системе, то система совместна и имеет единственное по теореме Кронекера – Капелли (§ 2.4. главы 2 [2]).

Пояснения к вычислению ранга:

1.При первом (1)преобразовании к элементам второй строки прибавить элементы первой, умноженные на (-2), а затем к элементам третьей строки прибавить элементы первой, умноженные на (-1).

2. При втором преобразовании (2)переставить местами второй и третий столбцы матрицы.

3.При третьем преобразовании (3)элементы второй строки прибавить к элементам третьей.

Итак, в результате этих преобразований получили систему уравнений

откуда, используя обратный ход метода Гаусса, найдем из третьего уравнения ; из второго уравнения и из первого уравнения . Решение системы (1;2;3).

Ответ: (1;2;3).

в)

Так как в данной системе число уравнений меньше числа неизвестных, то система не может иметь единственного решения, она либо несовместна, либо имеет множество решений. Выпишем расширенную матрицу и выполним эквивалентные преобразования.

.

Пояснения к решению:

1. Переставить местами 1-й и 4-й столбцы.

2. Первую строку умножить на (-2), затем на (-7) и прибавить ко 2-й и к 3-й строкам.

3. Умножить вторую строку на (-1), третью разделить на (-5). Получилось две одинаковых строки.

4. Выбросить одну из одинаковых строк.

В матрице не получилось противоречивой строки, значит система совместна и имеет множество решений, так как число строк меньше числа неизвестных по теореме Кронекера – Капелли (§ 2.4. главы 2 [2]).

Система, соответствующая последней матрице, имеет вид:

В качестве основных неизвестных можно взять неизвестные, соответствующие столбцам отличного от нуля минора 2-го порядка, приведенного к треугольному виду, остальные неизвестные перенести в правую часть.

подставить x₂ в x_4.

- множество решений.

Если придавать различные значения неизвестным x₁ и x₃, то каждый раз будут получаться новые значения неизвестных x₂ и x₄, те новые решения.

Пусть

Замечания. Это не единственные формулы общего решения. Если над расширенной матрицей выполнить другие эквивалентные преобразования, то формулы для общего решения получатся другие.

Ответ: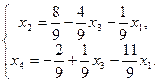

Задача 4

В ромбе ABCD известны координаты вершин А и С и тангенс внутреннего угла С. Найти уравнения диагоналей и сторон, координаты двух других вершин, а также площадь этого ромба, если А(1,10), С(7,2), . Сделать чертеж.

 

Решение

Изобразим графически положение ромба в прямоугольной системе координат ХОУ:

Зная координаты вершин А и С запишем уравнение диагонали АС как уравнение прямой,

 

Рисунок 1 – Схематичный чертеж

 

 

проходящей через две заданные точки: ;

В форме общего уравнения прямой оно примет вид

4х + 3у – 34 =0,

а в форме уравнения прямой с угловым коэффициентом перепишется как

, откуда К_АС =

 

Так как в ромбе диагонали взаимно перпендикулярны, то угловой коэффициент диагонали BD будет равен К_ВD =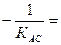

Само же уравнение диагонали BD найдем как уравнение прямой, проходящей через заданную точку в направлении, определяемом угловым коэффициентом К_BD.

В качестве «заданной точки» возьмем точку Е пересечения диагоналей ромба, которая лежит на середине отрезка АС, вследствие чего:

Е (4,6)

Итак, уравнение диагонали BD запишем в виде у – 6 = (х – 4),

Откуда у = х + 3 или 3х – 4у + 12 = 0.

Чтобы найти уравнение сторон ромба, надо определить только угловые коэффициенты К_АВ = К_CD и К_ВС = К_AD прямых, на которых эти стороны лежат, ибо точки, через которые эти прямые проходят, известны – это вершины А и С ромба.

Для определения указанных угловых коэффициентов воспользуемся формулой:

 

(*)

позволяющей вычислять тангенс угла φ между двумя заданными прямыми по их угловым коэффициентам К₁ и К₂; при этом угол φ отсчитывается против часовой стрелки от прямой у = К₁х + b₁ до прямой у = К₂х + b₂. Формула (*) оказывается удобной, потому что уравнение диагонали АС уже найдено (и, следовательно, известен ее угловой коэффициент К_АС), а положение сторон ромба относительно этой диагонали однозначно определяется внутренними углами А и С, которые равны между собой и для которых по условию известен их тангенс ().

Так диагонали ромба делят его углы пополам, то, положив (рисунок 1), из формулы для тангенса двойного угла при tg 2φ = 4/3 найдем tg φ:

 

Положим z = tg φ; тогда , откуда 2z² + 3z – 2 = 0;

корнями этого квадратного уравнения являются z₁ = и z₂ = -2; но так как угол φ в ромбе всегда острый, корень z₂ = -2 отбрасываем и получаем в итоге, что tg φ = .

Угол φ является углом между прямыми ВС и АС, с одной стороны, и прямыми АС и CD – с другой (рисунок 1).

Потому в первом случае по формуле (*) имеем

 

, откуда при К_АС = находим К_ВС = .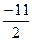

 

Во втором случае по формуле (*) имеем

К_CD – К_AC 4 1

½ =, откуда при К_АС = - находим К_CD = -.

1 + К_CDК_AC 3 2

Так как противоположные стороны ромба параллельны, то тем самым мы определили угловые коэффициенты всех его сторон.

К_CD = K_AB = - ½; K_BC = K_AD = - 11/2.

Зная теперь эти угловые коэффициенты и координаты вершин А и С, по уже использовавшимся выше формулам найдем уравнения прямых АВ, CD, BC и AD.

Уравнение АВ: у – 10 = - ½ (х – 1), откуда х + 2у – 21 = 0.

Уравнение CD: у – 2 = - ½ (х – 7), откуда х + 2у – 11 = 0.

Уравнение ВС: у – 2 = - 11/2 (х – 7), откуда 11х + 2у – 81 = 0.

Уравнение AD: у – 10 = - 11/2 (х – 1), откуда 11х + 2у – 31 = 0.

Вершины ромба являются точками пересечения его соответствующих сторон. Поэтому их координаты найдем путем совместного решения уравнений этих сторон.

Для вершины В:

х_В + 2у_В – 21 = 0 => В (6; 7,5)

11х_В + 2у_В – 81 = 0

 

Для вершины D:

11х_D + у_D – 31 = 0 => D (2; 4,5)

x_D + 2 y_D – 11 = 0

Координаты этих точек удовлетворяют ранее найденному уравнению

3х – 4у + 12 = 0 диагонали BD, что подтверждает их правильность. Уточним теперь положение точек В и D на чертеже и завершим построение последнего.

Площадь ромба вычислим по формуле S = ½ d₁d₂, где d₁ и d₂ – диагонали ромба.

Полагая d₁ = |АС|, а d₂ = |BD|, длины этих диагоналей найдем как расстояния между соответствующими противоположными вершинами ромба:

d₁ =

d₂ =

В итоге площадь ромба будет равна S = ½ ∙ 10 ∙ 5 = 25 кв.ед.