КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА
Кафедра «Высшая математика»
ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА,
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Методические указания к практическим занятиям
РПК «Политехник»
Волгоград
УДК 512.8 +514 (07)
Л 59
Линейная и векторная алгебра, аналитическая геометрия: Методические указания к практическим занятиям / Сост. В. Ф. Казак, Н. В. Гнедова; Волгоград. гос. техн. ун–т. – Волгоград, 2005. – 39 с.
Изучаются основные понятия линейной алгебры, векторной алгебры, аналитической геометрии на плоскости и в пространстве. Материал включает в себя практические упражнения и задания для самостоятельной работы.
Предназначены для студентов направлений 552900, 551200.
Ил. 13.
Рецензент У. А. Бурцева
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Составители: Вячеслав Федорович Казак,
Нина Васильевна Гнедова
Линейная и векторная алгебра, аналитическая геометрия
Методические указания к практическим занятиям
Под редакцией авторов
Темплан 2005 г., поз. № 37.
Подписано в печать 28. 04. 2005 г. Формат 60×84 1/16.
Бумага потребительская. Гарнитура ”Times“.
Усл. печ. л. 2,44. Усл. авт. л. 2,25.
Тираж 100 экз. Заказ
Волгоградский государственный технический университет
400131 Волгоград, просп. им. В. И. Ленина, 28.
РПК «Политехник»
Волгоградского государственного технического университета
400131 Волгоград, ул. Советская, 35.
 ©
| Волгоградский |
| государственный | |
| технический | |
| университет, 2005. |
Введение.
Методические указания предназначены для проведения практических занятий по математике для студентов, обучающихся по направлениям 552900 и 551200.
Цель данной работы – научить и закрепить навыки самостоятельного применения теоретических положений к решению практических задач.
Практическое занятие № 1 на тему:
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКА
1.1. ПРАВИЛО ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ ВТОРОГО ПОРЯДКА.
Примеры:
1. 
2. 
3. 
4. 
Вычислить самостоятельно:
a) 
б) 
в) 
г) 
д) 
е) 
Ответы а) – 9 б) 0 в) 0
г) – 2 д) 0 е) –2
1.2. ПРАВИЛО ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ ТРЕТЬЕГО ПОРЯДКА.
Примеры:
1. 
2. 
3. 
4. 
Вычислить самостоятельно:
a) 
б) 
в) 
г) 
д) 
е) 
Ответы а) – 18 б) 8 в) 0
г) 5 д) 0 е) 0
Практическое занятие № 2 на тему:
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ ПО
ПРАВИЛУ КРАМЕРА.
2.1. РЕШЕНИЕ СИСТЕМ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ
Для системы 
составляем главный определитель
и вычисляем его.
Затем составляем дополнительные определители:
, 
и вычисляем их.
По правилу Крамера решение системы находят по формулам:
; 
, если 
.
Примеры:
1) 
Ответ: (5;–4)
2) 
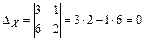
Так как все три определителя равны нулю, то система имеет бесконечное множество решений: 
3) 
.
Так как главный определитель равен нулю, а хотя бы один из дополнительных определителей не равен нулю, то система решений не имеет.
4) 
По формулам Крамера находим:
Ответ: (0; 0)
Решить системы самостоятельно:
a) 
б) 
в) 
Ответы: а) нет решения
б) бесконечное множество решений
в) (14; –19)
2.2. РЕШЕНИЕ СИСТЕМ ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ТРЕМЯ НЕИЗВЕСТНЫМИ
Для системы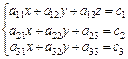 
составляем главный определитель
и вычисляем его.
Затем составляем дополнительные определители
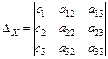
и вычисляем их.
По правилу Крамера решение системы находят по формулам
; 
; 
,если 
Примеры:
1) 
Вычислим:
По формулам Крамера находим:
Ответ: (1; 2; 3)
2) 
Вычислим:
Так как главный определитель 
, а хотя бы один дополнительный не равен нулю (в нашем случае 
), то решения у системы нет.
3) 
Вычислим:
Так как все определители равны нулю, то система имеет бесконечное множество решений, которое можно найти так 
Решите самостоятельно системы:
а) 
б) 
Ответ: а) (1; 2; 5) б) 
; 
; 
Практическое занятие № 3 на тему:
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ И ЕГО ПРИЛОЖЕНИЕ
1. Если дан 
и 
, то скалярное произведение находим по формуле: 
∙ 
2.Если 
, то скалярное произведение этих двух векторов находим по формуле 
Примеры:
1. Даны два вектора 
и 
Их скалярное произведение находим так:
.
2. Даны два вектора:
={2;3;–4} 
={1; –5; 6}
скалярное произведение находят так:
3. 
, 
3.1 НАХОЖДЕНИЕ РАБОТЫПОСТОЯННОЙ СИЛЫНА ПРЯМОЛИНЕЙНОМ УЧАСТКЕ ПУТИ
Примеры:
1) Под действием силы в 15Н тело переместилось по прямой на 2 метра. Угол между силой и направлением перемещения a=600. Вычислить работу силы по перемещению тела.
Дано: 
Решение: 
2) Дано: 
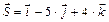
Найти А.
Решение: 
3) Из точки М(1; 2; 3) в точку N(5; 4; 6) переместилось тело под действием силы 60Н. Угол между направлением силы и вектором перемещения a=450. Вычислить работу, совершаемую этой силой.
Решение: находим вектор перемещения 
Находим модуль вектора перемещения:
По формуле 
находим работу:
3.2 ОПРЕДЕЛЕНИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ
.
Два вектора ортогональны, если 
, то есть
так как 
Примеры:
1) 
– не ортогональны
2) 
– ортогональны
3) Определить, при каком a векторы 
и 
взаимно-ортогональны.
Так как 
, то 
, значит
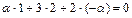
Решите самостоятельно:
а) 
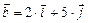. Найти их скалярное произведение.
б) Вычислить, какую работу производит сила 
, если точка ее приложения, двигаясь прямолинейно, переместилась из точки M (5; -6; 1) в точку N (1; -2; 3)
в) Определить, ортогональны ли вектора 
и
Ответы: а) 1 б) 16 в) да
3.3.НАХОЖДЕНИЕ УГЛА МЕЖДУ ВЕКТОРАМИ
Примеры:
1) 
. Найти 
.
Решение:
Находим 
подставляем в формулу:
.
1). Даны вершины треугольника А(3; 2; –3), В(5; 1; –1), С(1; –2; 1). Найти угол при вершине А.
Решение:
Находим 
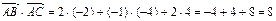
Подставим в формулу: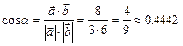 
Решите самостоятельно:
Даны вершины треугольника А(3; 5; -2), В(5; 7; -1), С(4; 3; 0). Определить внутренний угол при вершине А.
Ответ: 90о
Практическое занятие № 4 на тему: