Примеры:
Задача № 1. Найти уравнение прямой, проходящей через точку А(-2; 3) параллельно прямой 
Решение:
1. Найдем угловой коэффициент прямой .
- это уравнение прямой с угловым коэффициентом и начальной ординатой (
). Поэтому 
.
2. Так как прямые MN и АС параллельны, то их угловые коэффициенты равны, т.е. 
.
3. Для нахождения уравнения прямой АС воспользуемся уравнением прямой, проходящей через точку с данным угловым коэффициентом:
. В эту формулу вместо 
и 
подставим координаты точки А(-2; 3), вместо 
подставим – 3. В результате подстановки получим:
Ответ: 
Задача №2. Найти уравнение прямой, проходящей через точку К(1; –2) параллельно прямой 
.
Решение:
1. Найдем угловой коэффициент прямой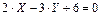 
.
- это общее уравнение прямой, которое в общем виде задается формулой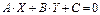 
. Сравнивая уравнения и 
находим, что А = 2, В = –3. Угловой коэффициент прямой, заданной уравнением 
, находится по формуле 
. Подставив в эту формулу А = 2 и В = –3, получим угловой коэффициент прямой MN. Итак, 
.
2. Так как прямые MN и КС параллельны, то их угловые коэффициенты равны: 
.
3. Для нахождения уравнения прямой КС воспользуемся формулой уравнения прямой, проходящей через точку с данным угловым коэффициентом 
. В эту формулу вместо 
и 
подставим координаты точки К(–2; 3), вместо 
подставим 
. В результате подстановки получим: 
Ответ: 
Задача № 3. Найти уравнение прямой, проходящей через точку К(–1; –3) перпендикулярно прямой 
.
Решение:
1. 
– это общее уравнение прямой, которое в общем виде задается формулой 
.
и 
находим, что А = 3, В = 4.
Угловой коэффициент прямой, заданной уравнением 
, находится по формуле: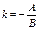 
. Подставив в эту формулу А = 3 и В = 4, получим угловой коэффициент прямой MN: 
.
2. Так как прямые MN и КD перпендикулярны, то их угловые коэффициенты обратно пропорциональны и противоположны по знаку:
.
3. Для нахождения уравнения прямой КD воспользуемся формулой уравнения прямой, проходящей через точку с данным угловым коэффициентом
. В эту формулу вместо 
и 
подставим координаты точки К(–1; –3), вместо 
подставим 
. В результате подстановки получим: 
Ответ: 
Решите самостоятельно:
1. Найти уравнение прямой, проходящей через точку К(–4; 1) параллельно прямой 
.
Ответ: 
.
2. Найти уравнение прямой, проходящей через точку К(5; –2) параллельно прямой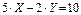 
.
Ответ: 
.
3. Найти уравнение прямой, проходящей через точку К(–2; –6) перпендикулярно прямой 
.
Ответ: 
.
4. Найти уравнение прямой, проходящей через точку К(7; –2) перпендикулярно прямой 
.
Ответ: 
.
5. Найти уравнение перпендикуляра, опущенного из точки К(–6; 7) на прямую 
.
Ответ: 
.
Практическое занятие № 6 на тему:
КРИВЫЕ ВТОРОГО ПОРЯДКА
6.1.ОКРУЖНОСТЬ
Примеры:
Задача № 1.
Написать уравнение окружности с центром С(4;-3), радиусом R=5 и построить её.
Решение. 
Каноническое уравнение окружнос-ти  с центром в точке С(a;b) и радиу-сом R имеет вид
Следовательно,a = 4; b= -3; R= 5
Тогда уравнение заданной окружности, будет 
Ответ: 
|
| ||
Задача № 2.
Определить координаты центра С и радиус R окружности
  и построить ее. Решение: из  канонического уравне-ния окружности с центром в точке С(a;b) и радиусом следует, что a = 0; b= -3;  16. откуда С(0;-3), R=4
 Ответ: С(0;-3), R=4
| 
| ||
Задача № 3.
Определить координаты центра С и радиус R окружности, заданной общим уравнением
 и построить ее.
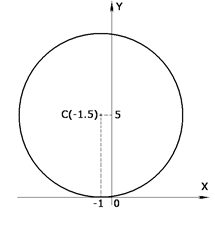
Решение: выделяя полные квадраты в левой части уравнения, получим:
 Сравнение полученного уравнения с каноническим уравнением
| 
| ||
окружности 
с центром в точке С(a;b) и радиусом R, показывает, что оно определяет окружность с центром в точке С(-1;5)и радиусом R=5.
Ответ: С(-1;5), R=5
Задача № 4.
Написать уравнение окружнос-ти, диаметром которой служит отрезок MN, где точка  M(2;-3) и точка N(-6;3) и построить ее.
Решение.
Координаты центра С(a;b) ок-ружности найдем как  координаты точки, делящий отрезок MN пополам:
|  
|
Следовательно С(-2;0). Радиус окружности
Тогда 
- искомое решение
Ответ: 
Решить самостоятельно:
Задача № 1. Составить уравнение окружности с центром в заданной точке С и данным радиусом R:
1) С (4;-7), R =5; 2) С (-6;3), R = 
3) С (-1;0), R =3; 4) С (0;-2), R = 
5) С (-1;0), R = 
;
Ответ: 1)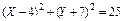 
2) 
3) 
4) 
5) 
Задача № 2. Для указанных окружностей определить координаты центра С и радиуса R:
1) 
2) 
3) 
Ответ: 1) С(4;-6), R =9; 2) С(-8;10), R =13; 3) С(0; 
), R = - 
Задача № 3. Как расположены по отношению к окружности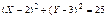 
следующие точки А(-1;-1); В(2;-3); С(-3;5); Д(4;-1);
Е (2;-2); F(5:7); G(1;0);
Ответ: точки А, Е и F лежат на окружности, точки В и С - вне окружности, точки Д и G-внутри окружности.
Задача № 4. Проходит ли окружность с центром в точке С(-5;7) и радиусом, равным 10, через точку М(-11;15)?
Ответ: да.
Задача № 5. Окружность с центром в точке С(12;-5) походит через начало координат. Составить уравнение этой окружности.
Ответ: 
Задача № 6. Известно, что концы одного из диаметров окружности находятся в точках М 
(2;-7) и М 
(-4;3)
Составить уравнение окружности.
Ответ: 
6.2.ЭЛЛИПС
Примеры:
Задача № 1. Найти оси, вершины, фокусы и эксцентриситет эллипса 
и построить его.
Решение:
Приведем данное уравнение эллипса к коническому виду 
, для чего свободный член перенесем вправо и разделим на него обе части уравнения. В результате получим 
отсюда 
.
Значит, длины полуосей равны соответственно a=5, b=3
А осей эллипса имеют координаты: 
.
Вершины эллипса имеют координаты: 
Поскольку b 
С 
По формуле 
находим эксцентриситет эллипса: 
По полученным данным построим эллипс:
Ответ: 
; 
;
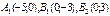
Задача № 2. Дан эллипс 
, получаем 
. Значит, длины полуосей равны соответственно a=5, b=3, а осей -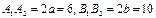 
.
Вершины же имеют координаты:
Так как b>a, то 
и 
следовательно b 
Тогда 
Откуда координаты фокусов 
а эксцентриситет 
, по полученным данным строим эллипс.
Ответ: 
, 
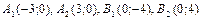
Задача № 3. Написать каноническое уравнение эллипса, проходящего через точку М(5;0), если фокальное расстояние равно 6.
Решение: Запишем каноническое уравнение эллипса 
Так как фокальное расстояние 
то С=3.
По условию точка М(5;0) принадлежит эллипса. Поэтому при подстановке координат точки М в уравнение эллипса, получим 
, откуда 
. Из равенства b 
находим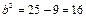 
,
Итак, искомым уравнением эллипса будет уравнение 
Решить самостоятельно:
Задача № 1. Напишите каноническое уравнение эллипса, если фокальное расстояние равно 8, а эллипс проходит через точку М(0;-3).
Ответ: 
Задача № 2. Составить простейшее уравнение эллипса, фокусы которого лежат на оси ОX, если его полуоси равны 4 и 5.
Ответ: 
Задача № 3. Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов:
1) 
2) 
Ответ: 1) 
; 
;
2) 
; 
;
Задача № 4. Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов:
1) 9x 
2) 16x 
3) 25x 
Ответ: 1) 
; 
;
2) 
; 
;
3) 
; 
;
Задача № 5. Составить простейшее уравнение эллипса, у которого длина малой оси равна 24, а один из фокусов имеет координаты (-5;0)
Ответ: 
Задача № 6. Расстояние между фокусами эллипса равно 30, а большая ось, лежащая на оси ОX, равна 34. Написать простейшее уравнение эллипса и найти его эксцентриситет.
Ответ: 
; 
Задача № 7. Составить простейшее уравнение эллипса, если известно,
Что один из фокусов находится в точке (6;0), а эксцентриситет 
Ответ: 
Задача № 8. Составить простейшее уравнение эллипса, если:
- между фокусами эллипса равно 6, а большая полуось равна 5;
- малая полуось равна 3, эксцентриситет равен
- большая полуось равна 10, эксцентриситет равен
Ответ: 1) 
; 2) 
3) 
6.3. ГИПЕРБОЛА
Примеры:
Задача № 1. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения асимптот гиперболы 
, и построить её.
Решение: Сравнивая данное уравнение с каноническим уравнением гиперболы 
. Имеем 
.Следовательно, соответственно a=3, b=4. Тогда, действительно ось гиперболы 
, а мнимая 
; координаты вершин А (-3;0), А 
(3;0).
Далее,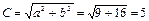 
; следовательно, фокусами гиперболы служат точки 
Эксцентриситет гиперболы вычисляется по формуле, следовательно, 
. Наконец, подставляя значения
а=3, b=4 в формулу 
, получаем уравнение асимптот гиперболы: 
и 
.
Ответ: 
; 
; А (-3;0), А 
(3;0), 
; 
Задача № 2. Найти оси, вершины, фокусы, эксцентриситет и уравнения асимптот гиперболы 16x 
и построить её.
Решение:
Перенесем свободный член вправо и разделим на него все члены данного уравнения, В результате получим простейшее уравнение гиперболы.
или 
Так как знак «-» стоит перед 
, то фокусы гиперболы расположены на оси Oy, а действительной осью 
, принадлежащая оси Oy. Сравнивая полученное уравнение с уравнением 
, имеем a=4, b=3, 
, координаты вершин 
(0;-3), 
(0;3). Далее, из формулы a 
получаем c 
т.е. с = 
=5.
Следовательно, фокусами гиперболы служат точки 
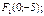
Эксцентриситет гиперболы вычисляется по формуле 
. Наконец, подставляя значения a = 4, b = 3 в формулу 
, получаем уравнение асимптот гиперболы: 
.
Ответ: 
; 
; 
(0;-3), 
(0;3). 
Задача № 3. Напишите каноническое уравнение гиперболы, если фокальное расстояние равно 30 и гипербола проходит через точку М(-9;0).
Решение:
Так как гипербола проходит через точку М(-9;0), то следовательно
М(-9;0)=А (-9;0) - вершина гиперболы, принадлежащая оси Оx, поэтому каноническое уравнение гиперболы имеет вид 
подставляя координаты точки М в указанное уравнение, получаем 
а 
Так как фокальное расстояние 
, то с=15, используя формулу 
получаем b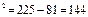 
. Тогда 
Решить самостоятельно:
Задача № 1. Найти оси, вершины, фокусы, эксцентриситет и уравнения асимптот следующих гипербол.
1) 
2) 
и построить их.
Ответ: 1) 
; 
; 
, 
2) 
; 
; 
(0;-6), 
(0;6) 
, 
Задача № 2. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения асимптот следующих гипербол.
1) 
2) 
2) 
и построить их.
Ответ: 1) 
; 
; 
, 
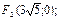
2) 
; 
; 
3) 
; 
; 
(0;-6), 
(0;6) 
, 
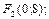
Задача № 3. Напишите уравнение гиперболы, если:
а) ее действительная полуось равна 4, а мнимая -14;
б) фокальное расстояние равно 16, а мнимая полуось -6;
в) фокальное расстояние равно 6, а 
=1,5
г) действительная полуось равна 8, а 
;
д) уравнение асимптоты 
, а действительная полуось равна 3, а 
Ответ: а)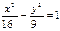 
б) 
в) 
г) 
д) 
е) 
Задача № 4. Составить простейшее уравнение гиперболы, действительная ось которой равна 6, а расстояние между фокусами равно 8. Написать уравнение сопряженной гиперболы.
Ответ: 
; 
Задача № 5. Напишите каноническое уравнение гиперболы, зная, что асимптоты её имеют уравнение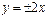 
, а фокусное расстояние равно 10.
Ответ: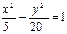 
Задача № 6. Сумма полуосей гиперболы равна 17, а эксцентриситет 
. Написать простейшее уравнение гиперболы и найти координаты её фокусов.
Ответ: 
, 
Задача № 7. Эксцентриситет гиперболы равен 
, а фокусами служат точки 
Составить Уравнение гиперболы и написать уравнение её асимптот.
Ответ: 
, 
.
6.4. ПАРАБОЛА.
Задача № 1. Определить координаты фокусов и составить уравнение директрисы параболы 
Решение:
Сравнивая это уравнение с уравнением 
, находим, что 2p=4, откуда 
. Таким образом, точка 
- фокусы параболы, а прямая 
, т. е. x=-1 или x+1=0 – её директриса.
Ответ: (1;0)
Задача № 2. Фокусы параболы с вершиной в начале координат лежит в точке F(0;-4). Написать уравнение этой параболы.
Решение: Так как F(0;-4) с Оy, то данная парабола симметрична относительно оси Оy, а ветви её направлены вниз. Кроме того О (0;0) -вершина параболы. Следовательно искомое уравнение параболы запишется в форме  . Поскольку,  . Тогда, уравнение параболы будет 
| 
|
Задача № 3. Директрисой параболы с вершиной в начале координат служит прямая 2x+5=0
Написать уравнение и найти координаты фокуса параболы.
Решение: Так как директрисой параболы с вершиной в начале координат служит прямая 2x+5=0 или 
, то ее фокус имеет координаты
, поэтому искомая кривая симметрична относительно оси Оx F(
) 
и ветви ее направлены вправо (абсцисса фокуса 
положительна). Следовательно, уравнение параболы имеет вид 
Так как 
то 
и уравнение параболы будет: 
, а координаты ее фокуса F(2,5;0)
Ответ: 
; F(2,5;0)
Задача №4. Написать уравнение параболы, симметричной относительно оси Оy, с центром в начале системы координат, если она проходит через точку В(1;-2).
Решение:
Так как парабола симметрична относительно оси Оy и имеет вершину в начале системы координат, то ее уравнение имеет вид 
. Поскольку точка В(1;-2) лежит на параболе, то ее координаты удовлетворяют параболы, т.е.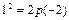 
,
Откуда 
, и, следовательно, 
- уравнение параболы.
Ответ: 
Задача № 5. Найти высоту арки моста длиной 24м, если арка имеет вид параболы, уравнение которой 
Решение:
Построим эскиз параболы 
в декартовой прямоугольной системе координат. Обозначим через h высоту моста, а через 
=24 - длину арки мосту. Тогда, А(12;-h) 
П: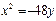 
.
Так как точка А принадлежит параболе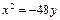 
, то ее координаты удовлетворяют уравнению параболы. Это дает возможность вместо текущих координат (x;y) подставить 
координаты данной точки в уравнение параболы. Тогда имеем 
Итак, высота арки моста 3 м.
Ответ: h=3
Задача № 6. Струя воды, направленная под углом к плоскости горизонта поднимается на высоту 2 м и падает в 12 м от наконечника шланга. Найти параболическую траекторию струи.
Решение: Свяжем параболическую траекторию струи с декартовой прямоугольной системой координат так, чтобы параболическая траектория была симметрична оси Оy, ветви были бы направлены вниз, а ее вершина лежала бы в начале координат.
Тогда уравнение такой параболической траектории имеет вид 
, точка А(6;-2) 
П: 
, следовательно, ее координаты удовлетво-ряют уравнению параболы. Подстановка координат точки А вместо 
текущих координат x и y параболы 
, дает равенство 
. Следовательно, 
- уравнение параболической траектории струи.
Ответ: 
Решить самостоятельно:
Задача № 7. Сечение рефлектора плоскостью проходящей через ось рефлектора, есть парабола. Написать ее уравнение, если ширина рефлектора 30 см, а глубина 20 см, (ось рефлектора совпадает с осью Ox)
Ответ: 
Задача № 8. Из отверстия, находящегося на поверхности земли вытекает вода струей, представляющей ветвь параболы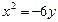 
. На каком расстоянии от края бака падает струя на землю, если высота отверстия
1,5 м?
Ответ: 3 м.
Задача № 9. Осевое сечение параболического зеркала является параболой 
Определить диаметр зеркала, если его «глубина» равна 18,75 см.
Ответ: 30 см.
Задача № 10. Камень брошенный под острым углом к плоскости горизонта, достиг наибольшей высоты 16 м., Описав параболическую траекторию, камень упал в 48 м., от точки бросания. Найти траекторию камня.
Ответ: 
.
Задача № 11 Найти параболу с вершиной в начале координат, если ее фокус лежит в точке а) F(3;0); б) F(-2;0); в) F(0;4); г) F(0;-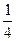 
)
Ответ: а) 
; б) 
; в) 
; г) 
Задача № 12 Найти параболы с вершиной в начале координат, если даны директрисы: а)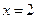 
; б) x=-5; в) y=3; г) y=-2;
Ответ: а) 
; б) 
; в) 
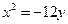; г) 
.
Задача № 13. Найти координаты фокуса и написать уравнение директрисы для каждой из парабол.
а) 
; б) 
; в) 
; г) 
. Построить эти параболы.
Ответ: а) F(2;0); x+2=0; б) F(-3;0); x-3=0; в) F(0; 
); 2y+5=0
г) F(0;-4); x-4=0
Задача № 14. Проверить, лежат ли точки А(2;-2) и В(1;2) на параболе 
Ответ: А лежат, В не лежат.
Задача № 15. Написать уравнение параболы с вершиной в начале координат, симметричной относительно оси Оx и проходящей через точку
А(4;-2)
Ответ: 
Задача № 16. Напишите уравнение параболы с вершиной в начале координат, если:
А) парабола расположена в верхней полуплоскости симметрично относительно оси ординат, а ее фокальный параметр равен 4;
Б) парабола расположена в нижней полуплоскости симметрично относительно оси ординат, а ее фокальный параметр равен 6;
В) парабола расположена в правой полуплоскости симметрично относительно оси ординат, а ее фокальный параметр равен 3;
г) парабола расположена в левой полуплоскости симметрично относительно оси ординат, а ее фокальный параметр равен 5.
Ответ а) 
; б) 
; в) 
; г) 
.
Практическое занятие № 7 на тему: