Тема: Элементы комбинаторики
Сколько чисел меньших, чем миллион можно написать с помощью цифр 3 и 7?
| 126 | |
Решение:
С помощью двух различных цифр можно записать  – шестизначных чисел,,
– шестизначных чисел,,  – пятизначных,
– пятизначных,  - четырехзначных
- четырехзначных  трехзначных чисел
трехзначных чисел 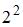 двузначных чисел,
двузначных чисел,  – однозначных чисел. Просуммируем эти композиции
– однозначных чисел. Просуммируем эти композиции 
Тема: Неориентированные графы
Матрица смежности графа, изображенного на рисунке 
имеет вид … 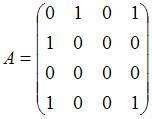
Решение: Матрицей смежности графа называют квадратную матрицу  размера
размера 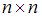 , строкам и столбцам которой соответствуют вершины помеченного графа (первый столбец (строка) отвечает первой вершине и т.д.), а ее элементы
, строкам и столбцам которой соответствуют вершины помеченного графа (первый столбец (строка) отвечает первой вершине и т.д.), а ее элементы  равны количеству ребер, инцидентных вершинам с номерами i и j. Согласно определению составляем матрицу смежности
равны количеству ребер, инцидентных вершинам с номерами i и j. Согласно определению составляем матрицу смежности 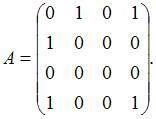
Тема: Операции над высказываниями
Нулевой набор у формулы  получается при следующих значениях переменных …
получается при следующих значениях переменных …  ,
, 
Тема: Декартово произведение множеств
Пусть заданы два множества:  ,
, 
Тогда геометрическая интерпретация множества  имеет вид …
имеет вид … 
Тема: Элементы комбинаторики
Вокруг костра сидят 12 разбойников. Каждый из них смертельно ненавидит двух ближайших соседей. С целью спрятать награбленное необходимо выделить 5 разбойников. Сколькими способами атаман может назначить пятерых так, чтобы между ними не было распрей?
| 12 | |
Решение:
12 разбойников разбиваются на две группы по 6 не враждующих между собой человек. Атаман может выбрать 5 человек из первой группы 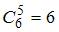 способами или 5 человек из второй группы тоже
способами или 5 человек из второй группы тоже 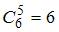 способами. Тогда по правилу суммы получим:
способами. Тогда по правилу суммы получим:  способов выбора 5 разбойников.
способов выбора 5 разбойников.
Тема: Операции над высказываниями
Отрицание высказывания  равносильно высказыванию …
равносильно высказыванию … 
Решение:
Высказывание  означает: неправда что х положительно, а значит
означает: неправда что х положительно, а значит 
Тема: Неориентированные графы
Эйлеровым является граф …

Решение:
Эйлеровым называют граф содержащий эйлеров цикл. Цикл называется эйлеровым, если он простой и содержит все ребра графа.
Критерий эйлеровости графа: граф называется Эйлеровым тогда и только тогда, когда степени всех его вершин четные.
Из представленных графов только этот граф имеет четные степени всех вершин.
Тема: Декартово произведение множеств
Декартово произведение отрезка  на отрезок
на отрезок 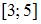 ….является прямоугольником с вершинами
….является прямоугольником с вершинами 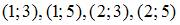
Решение:
Декартовым произведением отрезка на отрезок является прямоугольник с вершинами 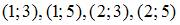
Тема: Элементы комбинаторики
На 10 карточках написаны буквы так, что из этих карточек можно получить слово ИСЧИСЛЕНИЕ. Сколько существует различных 10-буквенных слов, которые можно образовать с помощью этих десяти карточек?
| 151200 | |
Решение:
Разобьем карточки на группы. Первая группа содержит букву И. Элементы ее неразличимы. Число элементов первой группы  . Вторую группу образуют карточки с буквой С. Число элементов второй группы
. Вторую группу образуют карточки с буквой С. Число элементов второй группы  . Третью группу образуют карточки с буквой Ч. Число элементов этой группы
. Третью группу образуют карточки с буквой Ч. Число элементов этой группы  . Четвертую группу образуют карточки с буквой Л, число элементов
. Четвертую группу образуют карточки с буквой Л, число элементов 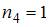 . Пятую группу образуют карточки с буквой Е. Число элементов
. Пятую группу образуют карточки с буквой Е. Число элементов  . Шестая группа состоит из карточек с буквой Н. Количество элементов этой группы
. Шестая группа состоит из карточек с буквой Н. Количество элементов этой группы 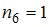 . Число различных 10-буквенных слов, образованных этими 10 карточками, совпадает с числом различных перестановок с повторениями и равно
. Число различных 10-буквенных слов, образованных этими 10 карточками, совпадает с числом различных перестановок с повторениями и равно 
Тема: Неориентированные графы
Из представленных графов полным является граф …
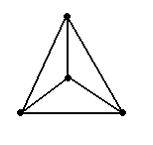
Решение:
Полным называют граф без петель и кратных ребер, в котором любые две вершины соединены ребром.
Тема: Операции над высказываниями
Из трех логических выражений:


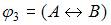
эквивалентными являются …  и
и 
Решение:
Составим таблицы истинности для 


Сопоставляя таблицы, видим, что 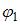 не эквивалентна формулам
не эквивалентна формулам  и
и 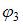 , а
, а  и
и 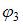 эквивалентны.
эквивалентны.
Тема: Декартово произведение множеств
Декартово произведение 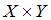 множеств
множеств  и
и  равно …
равно … 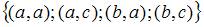
Тема: Декартово произведение множеств
Декартово произведение множеств 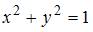 и
и  представляет собой …
представляет собой …

| окружность 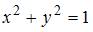 , лежащую в плоскости , лежащую в плоскости 
|
Тема: Неориентированные графы
Для графа, изображенного на рисунке,
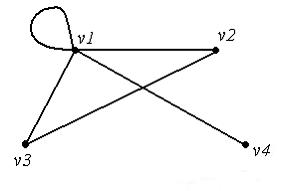
степень вершины  равна …
равна …

| |||
Решение:
Степенью вершины называют удвоенное количество петель, инцидентных этой вершине, плюс количество остальных инцидентных ей ребер. То есть степень вершины  равна пяти.
равна пяти.
Тема: Элементы комбинаторики
На школьном вечере присутствуют 5 девушек и 6 юношей. Выбрать из них 2 пары для танца можно ___ способом(-ами).
| 300 | |
Решение:
Сначала в произвольном порядке выбираем двух юношей из шести 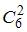 способами (сочетания 2 из 6), затем выбираем для них девушек, причем теперь порядок выбора важен. Число способов выбрать двух девушек из пяти равно
способами (сочетания 2 из 6), затем выбираем для них девушек, причем теперь порядок выбора важен. Число способов выбрать двух девушек из пяти равно  (размещения 2 из 5).
(размещения 2 из 5).
Тогда число способов для выбора двух пар по правилу произведения равно:

Тема: Операции над высказываниями
На вопрос, кто из трех учащихся изучал логику, был получен правильный ответ: если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй. Тогда логику …

| изучал третий учащийся | ||
| изучал второй учащийся | |||
| изучал первый учащийся | |||
| никто из учащихся не изучал |
Решение:
Обозначим через a, b, c высказывания, состоящие соответственно в том, что первый, второй, третий учащиеся изучали логику. Запишем условие задачи с помощью a, b, c и логических операций. Получим выражение  . Известно, что это высказывание истинно. Составим таблицу истинности полученного выражения:
. Известно, что это высказывание истинно. Составим таблицу истинности полученного выражения:

Только в предпоследней строке получившееся выражение принимает истинное значение, а все остальные значения ложны. При этом высказывания a и b ложны, а c – истинно. Значит, логику изучал только третий учащийся.
Тема: Операции над высказываниями
Высказывание « » означает, что …
» означает, что …

| « – любое число» – любое число»
| ||
« принадлежит интервалу принадлежит интервалу  » »
| |||
« принадлежит промежутку принадлежит промежутку 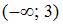 » »
| |||
« не существует» не существует»
|
Решение:
Высказывание « » – это дизъюнкция двух неравенств, и решением является объединение промежутков:
» – это дизъюнкция двух неравенств, и решением является объединение промежутков:  . То есть
. То есть  – любое число.
– любое число.
Тема: Декартово произведение множеств
Даны множества 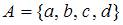 ,
,  и
и 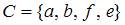 . Тогда число элементов декартова произведения множеств
. Тогда число элементов декартова произведения множеств  равно…
равно…

| |||
Решение:
Декартово произведение множеств – это множество, состоящее из упорядоченных пар элементов, первым элементом которых являются элементы первого множества, вторым – элементы второго, то есть 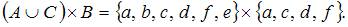
Множество, состоящее из шести элементов, умножается на множество из четырех элементов, тогда по свойству декартова произведения получается множество, состоящее из 24 элементов.
Тема: Неориентированные графы
Для графа, изображенного на рисунке,
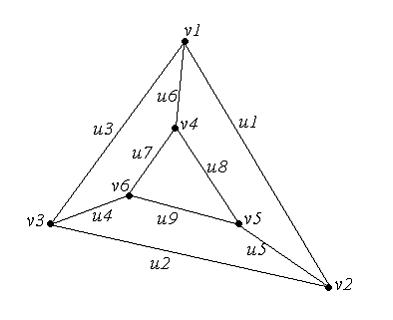
гамильтоновым циклом является маршрут …

| 
| ||
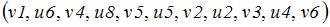
| |||

| |||

|
Решение:
Цикл называется гамильтоновым, если он простой и содержит все вершины графа.
Для данного графа гамильтоновым циклом служит, например, маршрут

Тема: Неориентированные графы
Матрица смежности графа, изображенного на рисунке

имеет вид …

| 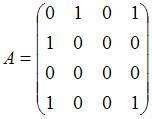
| ||

| |||
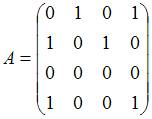
| |||
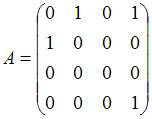
|
Решение:
Матрицей смежности графа называют квадратную матрицу  размера
размера 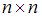 , строкам и столбцам которой соответствуют вершины помеченного графа (первый столбец (строка) отвечает первой вершине и т.д.), а ее элементы
, строкам и столбцам которой соответствуют вершины помеченного графа (первый столбец (строка) отвечает первой вершине и т.д.), а ее элементы 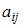 равны количеству ребер, инцидентных вершинам с номерами i и j. Согласно определению составляем матрицу смежности
равны количеству ребер, инцидентных вершинам с номерами i и j. Согласно определению составляем матрицу смежности 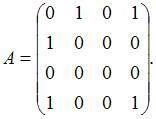
Тема: Декартово произведение множеств
Даны множества 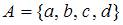 ,
,  и
и 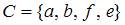 . Тогда число элементов декартова произведения множеств
. Тогда число элементов декартова произведения множеств  равно…
равно…

| |||
Решение:
Декартово произведение множеств – это множество, состоящее из упорядоченных пар элементов, первым элементом которых являются элементы первого множества, вторым – элементы второго, то есть 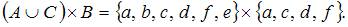
Множество, состоящее из шести элементов, умножается на множество из четырех элементов, тогда по свойству декартова произведения получается множество, состоящее из 24 элементов.
Тема: Элементы комбинаторики
Сколько чисел меньших, чем миллион можно написать с помощью цифр 3 и 7?
| 126 | |
Решение:
С помощью двух различных цифр можно записать  – шестизначных чисел,
– шестизначных чисел,  – пятизначных чисел,
– пятизначных чисел,  – четырехзначных чисел,
– четырехзначных чисел,  – трехзначных чисел,
– трехзначных чисел,  – двузначных чисел,
– двузначных чисел, 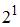 – однозначных чисел. Просуммируем эти композиции
– однозначных чисел. Просуммируем эти композиции  .
.
Тема: Операции над высказываниями
Формулой, равносильной формуле  , является …
, является …

| 
| ||

| |||

| |||

|
Решение:

Тема: Операции над высказываниями
Таблица истинности для формулы 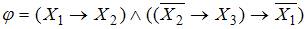 представляет собой …
представляет собой …

| 
| ||

| |||

| |||

|
Решение:

Тема: Неориентированные графы
Эйлеровым является граф …

| 
| ||

| |||

| |||
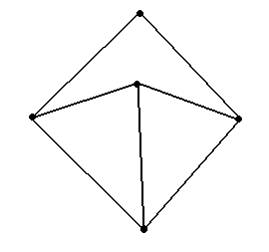
|
Решение:
Эйлеровым называют граф содержащий эйлеров цикл. Цикл называется эйлеровым, если он простой и содержит все ребра графа.
Критерий эйлеровости графа: граф называется Эйлеровым тогда и только тогда, когда степени всех его вершин четные.
Из представленных графов только граф

имеет четные степени всех вершин.
Тема: Операции над высказываниями
Высказывание « » означает, что …
» означает, что …

| « – любое число» – любое число»
| ||
« принадлежит интервалу принадлежит интервалу  » »
| |||
« принадлежит промежутку принадлежит промежутку 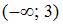 » »
| |||
« не существует» не существует»
|
Решение:
Высказывание « » – это дизъюнкция двух неравенств, и решением является объединение промежутков:
» – это дизъюнкция двух неравенств, и решением является объединение промежутков:  . То есть
. То есть  – любое число.
– любое число.
Тема: Элементы комбинаторики
В урне находятся 10 белых, 15 красных, 20 голубых шаров. Все шары пронумерованы. Сколькими различными способами можно взять из урны три шара разных цветов?
| 3000 | |
Решение:
Возьмем один белый шар. Это действие можно выполнить 10 способами (по числу различных белых шаров в урне). К выбранному белому шару присоединим красный шар, который можно взять 15 различными способами (по числу различных красных шаров в урне). К выбранной присоединим голубой шар, который можно взять 20 способами (по числу различных голубых шаров в урне). Таким образом, можно образовать различные тройки разноцветных шаров. Число различных способов выбора троек разноцветных шаров совпадает с числом различных трех действий и по правилу умножения равно:

Тема: Неориентированные графы
Для графа G, изображенного на рисунке,

матрица смежности имеет вид …

| 
| ||
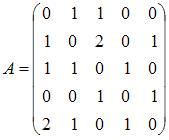
| |||

| |||

|
Тема: Операции над высказываниями
Отрицанием высказывания «Если я сдам зачет, то пойду в кафе с друзьями или на вечеринку» является высказывание:

| «Я сдам зачет и не пойду ни в кафе с друзьями, ни на вечеринку» | ||
| «Если я не сдам зачет, то не пойду в кафе с друзьями или не пойду на вечеринку» | |||
| «Если я не сдам зачет, то, несмотря ни на что, пойду в кафе с друзьями или на вечеринку» | |||
| «Я не сдам зачет и не пойду ни в кафе с друзьями, ни на вечеринку» |
Решение:
Введем простые высказывания: A – «я сдам зачет», B – «пойду в кафе с друзьями», C – «пойду на вечеринку».
Тогда высказывание «Если я сдам зачет, то пойду в кафе с друзьями или на вечеринку» имеет вид  .
.
Отрицание этого высказывания  .
.
Получаем высказывание: «Я сдам зачет и не пойду ни в кафе с друзьями, ни на вечеринку».
Тема: Элементы комбинаторики
Из колоды в 36 карт наудачу без возвращения вынимают по одной карте 3 раза. Сколько существует различных способов получения трех карт, среди которых на первых двух местах – бубны, а на третьем – пики.
| 648 | |
Решение:
В колоде 9 бубен и 9 пик. Получение тройки карт «бубны, бубны, пики» можно рассматривать как результат двух действий. Первое действие – получение на первых картах «бубны, бубны». Поскольку порядок карт существенен, то число различных способов осуществления первого действия совпадает с числом размещений из 9 элементов по 2:  .
.
Второе действие – взятие «пики» на третьем месте. Число способов выполнить второе действие равно 9 (по количеству «пик»). По правилу умножения, получим: 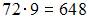 .
.
Тема: Декартово произведение множеств
Декартово произведение отрезка  на отрезок
на отрезок 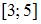 …
…

| является прямоугольником с вершинами 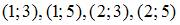
| ||
является отрезком 
| |||
| равно 2 | |||
| равно 13 |
Решение:
Декартовым произведением отрезка  на отрезок
на отрезок  является прямоугольник с вершинами
является прямоугольник с вершинами 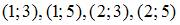
Тема: Неориентированные графы
Матрица инцидентности графа, изображенного на рисунке

имеет вид …

| 
| ||

| |||

| |||

|
Тема: Элементы комбинаторики
В урне находятся 5 белых, 7 красных, 6 голубых шаров. Сколько существует способов извлечь 9 шаров так, чтобы среди них оказалось 2 белых, 3 красных и 4 голубых шара?
| 5250 | |
Решение:
Всего в урне 18 шаров. Сначала выберем два белых шара из 5 белых шаров. Это действие можно выполнить  способами. Второе действие состоит в выборе трех красных шаров из 7 красных шаров. Это действие можно выполнить
способами. Второе действие состоит в выборе трех красных шаров из 7 красных шаров. Это действие можно выполнить  способами. Третье действие состоит в выборе четырех голубых шаров. Оно может быть выполнено
способами. Третье действие состоит в выборе четырех голубых шаров. Оно может быть выполнено  способами.
способами.
По правилу умножения получим: 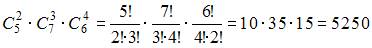
o Информатика (2)
o Физика (2)
o Русский язык (0)
o Обществознание (0)
o История (0)
o Английский язык (2)
o Биология (0)
o География (0)
o Химия (0)
o Экономика (1)
o Презентации PowerPoint
o Расчетки
o Материалы
o Шпаргалки
o Лабораторные работы
o Разное
o Курсовые
o Дипломы
o Решение задач
o Видеоуроки
o Юмор
o Это интересноКультурология
o Метрология
o Безопасность жизнедеятельности
o Философия
o Информатика
o КП РФ
o Политология
o История
o Материаловедение i-exam
o Психология и педагогика
o Математика
o Отправка материалов!
o Физика
o Экономика