Глава 4. Реконструкция истории погружения осадочного бассейна
Реконструкция истории погружения осадочного бассейна осуществляется на основе следующего ряда данных (Doligez et al., 1986; Ungerer, 1990; Галушкин, 1990; Ершов, Волож, 2004; Makhous and Galushkin, 2005): а) описание современного геологического разреза, включающее порядок залегания, глубину, мощность и литологический состав пород каждого слоя; б) описание перерывов и несогласий в разрезе; в) датировку абсолютного возраста геологических единиц в разрезе; г) определение палеоглубин морского бассейна; д) соотношение, описывающее уплотнение пород с глубиной, вклющее изменение с глубиной пористости пород слоя. Пористость осадочных пород существенно влияет на значения их теплофизических параметров. Это один из ключевых параметров в реконструкциях истории погружения осадочных бассейнов. В процессе консолидации при погружении в бассейне мощность слоя осадков может уменьшиться в 2-3 раза по сравнению с отложенной у поверхности. В этой главе обсуждаются физический смысл понятия пористости, процессы, влияющие на её изменение с глубиной, алгоритмы, описывающие эти изменения в системах моделирования бассейнов, а также рассматриваются тесно связанные с пористостью проблемы формирования проницаемости пород и генерации аномальных давлений в осадочной толще нефтегазоносных бассейнов.
Уплотнение и пористость осадочных пород
4.1.1 История погружения бассейна и пористость пород
С погружением бассейна осадочные породы сжимаются, уменьшая объём порового пространства и высвобождая часть поровых вод. В системах моделирования бассейнов вместо вычисления скоростей смещения твердого скелета обычно имеют дело с вертикальными деформациями элементов сети (скелета) при уплотнении пород. При этом процесс консолидации осадков рассматривается как медленное вертикальное адиабатическое сжатие области, заполненной осадочным материалом (Рис. 1-4). Каждый из элементов осадочного слоя уменьшается (сжимается) в размераx в соответствии с изменением пористости данной породы с глубиной. Процесс консолидации рассматривается в обычном предположении (Perrier and Qublier, 1974), что изменение объёма твердой матрицы пород под действием лежащей выше нагрузки пренебрежимо мало по сравнению с уменьшением объёма их порового пространства:
Рис. 1-4. Формирование области счёта и граничные условия в численной реконструкции истории погружения и эволюции термических условий осадочных бассейнов в системе моделирования ГАЛО.
Dz1 (1-j(z1)) = Dz2 (1-j(z2)) (4-1)
где j(z)- пористость на глубине z и Dz1 и Dz2 - толщины слоя на глубинах z1 and z2, соответственно. В уравнении (4-1) слева стоит объём элементарного слоя на глубине z1 (на единицу площади), справа объём того же слоя на глубине z2. В пределах интервала времени (Dt) отложения элементарного слоя осадков Dz на поверхности бассейна консолидация лежащих ниже осадков (под нагрузкой этого слоя Dz) предполагается мгновенной, то есть следующей сразу же после отложения элементарного слоя Dz (Рис. 1-4). Это некоторое приближение, так как на самом деле в ответ на изменение давления и температуры породы уплотняются не мгновенно а в течение некоторого интервала времени, причём фронт уплотнения будет мигрировать со временем вниз. Задержка этого процесса по глубине и времени зависит от способности поровой жидкости покидать породу. Однако, для многих бассейнов с широким интервалом скоростей осадконакопления это приближение оправдано. Оно позволяет избежать сложных вычислений в рамках теории консолидации сред с такими плохо определёнными параметрами пород как проницаемость, вязкость порового флюида и др. (см. ниже). Считают, что в периоды эрозии и перерывов в осадконакоплении мощности осадков Dzk не меняются. Соотношение (4-1), отражающее факт неизменности объёма скелета при погружении породы на глубину, служит основой так называемой процедуры “разуплотнения” (decompaction), применяемой для восстановления истории погружения осадочных бассейнов во всех пакетах по моделированию бассейнов. В этой процедуре процесс формирования осадочной толщи бассейна рассчитывается с момента зарождения бассейна, при этом вычисляется уменьшение пористости лежащих ниже пород, вызванное отложением очередного элементарного слоя осадков на поверхности бассейна.
4.1.2 Изменение пористости с глубиной
Пористость осадочных пород является ключевым параметром в процедуре “разуплотнения” и существенно меняется с глубиной захоронения и литологией пород (Рис.2-4).
Рис. 2-4 Изменение пористости с глубиной в разрезе скв. 411 Уренгойской площади Западно-Сибирского бассейна (Galushkin, 1997).
Вместе с литологическим составом и температурой пород пористость существенно влияет на значения теплофизических параметров и лежит в основе реконструкции истории погружения бассейна. Соотношение (4-1) позволяет восстановить историю формирования осадочной толщи бассейна, если знать закон изменения пористости пород с глубиной.
Строго говоря, пористость является функцией эффективного напряжения в скелете пород, s.
j = j (s), где s = Sg – P (4-2)
Это соотношение означает, что в осадочной толще вес вышележащего слоя осадков Sg, (overburden pressure или давление от нагрузки осадков), поддерживается совместным действием эффективных напряжений скелета, s, передающихся от кристалла к кристаллу на контактах зёрен, и давлением жидкости в порах, P:
Sg = s + P (4-3)
Вес столба осадков можно выразить через среднюю плотность осадков, насыщенных водой, rb, и высоту столбца осадков, z:
= rb×g×z (4-4)
Следовательно, вертикальная нагрузка осадков (4-3) должна разделяться между P и s. Если l = P / Sg есть отношение давления поровой жидкости к давлению нагрузки осадков, то для гидростатического давления (самая низкая величина порового давления):
P = rw×g×z (4-5)
значение l будет равно отношению плотности жидкости к средней плотности осадков:
l = P / Sg = rw / rb (4-6)
Это так называемый случай нормального давления. При l > rw / rb поровая жидкость находится при давлении выше гидростатического. Для гидростатического давления поровой жидкости из (4-3, 4-5) получаем:
s = (rb - rw)×g×z (4-7)
Выражение (4-7) гласит, что величина эффективных напряжений в скелете, вызванных уплотнением, определяется глубиной погружения и разностью между средней плотностью насыщенных водой осадков и плотностью воды.
При моделировании бассейнов обычно используют заданные законы изменения пористости с глубиной j = j(z). Так, Бэтке (Bethke, 1985) показал, что соотношению (4-2) удовлетворяет эмпирическая экспоненциальная зависимость пористости от глубины:
j = j(0) exp(-z / B) (4-8)
где j(0) - пористость осадков при их отложении на поверхности (среднее значение для верхних 100-150 м осадков данной литологии), B - масштаб изменения пористости с глубиной. Эта зависимость справедлива в случаях, когда градиент аномально высоких поровых давлений (АВПД) не превышает гидростатический более чем на 100 м/ км (Person and Garvon, 1992). В этом случае смещения скелета вычисляются из соотношения (4-1). Такое приближение широко используется в процедурах моделирования бассейнов (Ungerer et.al 1990; Welte et.al 1997; и др.). Оно позволяет избежать громоздкиx вычислений в рамкаx теории консолидации неоднородной пористой cреды с таким сильно изменчивым и трудно определяемым параметром как проницаемость пород. Следует подчеркнуть при этом, что параметр z в соотношении (4-8) для вычисления пористости есть не просто текущая глубина погружения породы, а что он является максимальной глубиной, достигнутой породой в истории её погружения. По этой причине пористость пород не будет меняться в периоды эрозии бассейна, когда давление от нагрузки вышележащих осадков уменьшается (Ungerer, 1990).
Ситуация, когда пористость пород в разрезе является однозначной функцией давления или глубины, является признаком нормального распределения порового давления в бассейне с глубиной. Тогда оно соответствует гидростатическому градиенту на данной глубине. Обзор механизмов генерации аномальных давлений в заключительной части этой главы, показывает, что возникновение АВПД относится к сравнительно тонким слоям слабо проницаемых пород и является относительно локальным событием как по времени, так и по месту своего проявления. В то же время значительная часть истории развития многих осадочных бассейнов протекает в отсутствии заметных аномальных поровых давлений в породах бассейна. По этой причине использование заранее известной зависимости пористости от давления или глубины является общепринятым в системах моделирования бассейнов (Nakayama and Lerche, 1987; Welte and Yalcin, 1988; Espitalie et al.,1988; Галушкин, 1988, 1990; Ungerer, 1990; Ungerer et al.,1990; Makhous et al., 1997; Makhous and Galushkin, 2005). Возможное влияние отклонений, вызванных локальными зонами АВПД, анализируется обычно в рамках приближённых решений (см. ниже) или соответствующим подбором масштаба уплотнения породы в соотношении (4-3).
Для нормально сжатых сред в системе ГАЛО предусмотрена возможность выбора из трёx вариантов изменения пористости с глубиной. Первый предполагает произвольную зависимость j(z), которая может отражать наблюдаемые вариации пористости для конкретных литологий в разрезах. Второй отражает довольно распространённый закон экспоненциального убывания пористости с глубиной, выражаемый формулой (4-8) (Sclater, Christie1980; Deming and Chapman, 1989; Ungere et.al 1990 и др.). И, наконец, третий вариант рассматривает линейный спад пористости с глубиной, применяющийся иногда для песчаных пород (Magara 1980; Ungere et.al 1990):
j(z) = 0. для z > B и j(z) = j(0)×(1 - z / B) для 0 £ z £ B (4-9)
В (4-9) z - глубина, В - масштаб изменения пористости с глубиной и j(0) - пористость осадочных пород у поверxности (среднее значение для верхних 100-150 м осадков данной литологии).
Таким образом, закон изменения пористости с глубиной задаётся в моделировании через параметры уплотнения пород слоя j(0) и B. Последние оцениваются либо по данным анализа измерений петрофизических свойств пород из кернов конкретных скважин, либо на основании среднемировых данных для основных литологических единиц, которые приведены в табл. 1-4 и получены изучением свойств пород из многих районах мира. В последнем случае необходимо иметь ввиду, что значения параметров уплотнения j(0) и B, взятые для конкретных типов пород из разных литературных источников, характеризуются заметным разбросом. Например поверхностная пористость j(0) для глин варирует от значения 0.75 в работе (Forbes et al 1991) до 0.60 в (Stockmal et al 1986; Beaumont et al 1982; Sclater and Christie 1980; и др.) при вариацияx в величине масштабного параметра В от 1.11 км в работе (Forbes et al 1991) до 2.0 км в статьях (Sclater and Christie 1980; Nielsen and Balling 1990; и др.).
Табл. 1-4 Средне-мировые значения петрофизических параметров основных осадочных фаций (Построена по данным работ Sclater and Christie, 1980; Gretener et,1981; Beaumont et al.,1982; Goff,1983; Hutchinson, 1985; Stockmal et al., 1986; Doligez et al., 1986; Deming and Chapman, 1989; Nielsen and Balling, 1990; Burrus and Anderbert, 1990; Ungerer et al., 1990; Ungerer, 1990; Forbes et al.,1991; Nyblade et al., 1996; Midttomme and Roaldset, 1999)
| N | порода | j(0) | B (км) | Km (Вт/м°К) | Al (oC-1) | Cv (МДж/м3°K) | rm (г/см3) | A (мкВт/м3) |
| Глина | 0.70 | 1.80 | 2.09 | 0.0005 | 2.26 | 2.70 | 2.09 | |
| вулканит | 0.50 | 3.27 | 2.01 | 0.0001 | 2.50 | 2.70 | 0.10 | |
| алевролит | 0.54 | 2.25 | 3.39 | 0.0020 | 2.68 | 2.66 | 1.21 | |
| песчаник | 0.40 | 3.00 | 5.44 | 0.0030 | 2.89 | 2.65 | 0.84 | |
| известняк | 0.60 | 1.90 | 2.97 | 0.0005 | 2.72 | 2.71 | 0.63 | |
| доломит | 0.50 | 2.00 | 4.61 | 0.0020 | 2.70 | 2.75 | 0.36 | |
| Соль | 0.00 | 0.01 | 5.86 | 0.0050 | 1.85 | 2.16 | 0.00 | |
| ангидрит | 0.35 | 0.90 | 5.44 | 0.0050 | 2.01 | 2.40 | 0.08 | |
| мергель | 0.65 | 1.84 | 2.60 | 0.0005 | 2.54 | 2.71 | 1.21 | |
| Уголь | 0.10 | 1.47 | 0.42 | 0.0001 | 1.00 | 1.40 | 0.00 |
Замечания: j(0) – средняя пористость верхних 0.-200 м осадочных пород, B – масштаб изменения пористости с глубиной в зависимости: j(z) = j(0) EXP(-z/B)), Km - теплопроводность матрицы пород при температуре T=0oC, Al – коэффициент температурного изменения матричной теплопроводности: Km(T)=Km / (1.+ Al×T(oC)), Cv – обьемная теплоемкость матрицы пород, rm – плотность матрицы пород, A – обьемная генерация радиогенного тепла в осадках.
Аналогично, для песчаников j(0) меняются от 0.40 в (Goff et al 1983; Forbes et al 1991) до 0.62 в (Beaumont et al, 1982) с вариациями в параметре В от 2.8 км в (Stockmal et al 1986) до 5 км в (Goff 1983). Ещё более значительны вариации для известняков: от 0.24 в (Hutchinson 1987) до 0.70 в (Sclater and Christie 1980) для j(0) и от 1.4 км до 6.25 км для параметра В. Такой разброс во многом связан с неопределённостью интервала глубин осреднения при оценках поверхностной пористости пород. Однако, ситуация облегчается наличием общей тенденции: в тех случаях, когда литературные данные по j(0) превосходят значения, приведённые в табл. 1-4, величина масштаба уплотнения (В) будет меньше, чем приведённая в таблице. В итоге получаются кривые уплотнения j(z) с разумным пересечением, хотя и не вполне идентичные друг другу. B целом, петрофизические параметры табл. 1-4 отражают среднемировые данные для рассматриваемого типа пород с тенденцией к описанию свойств осадочных пород, отложенных в условиях морских бассейнов, типа Северного моря (Sclater and Christie 1980; Gretener, 1981; Deming and Chapman, 1989; и тд.). Эти значения используются как первое приближение для пород реального осадочного бассейна, но желателен соответствующий контроль параметров по данным бурения.
4.1.3 Параметры уплотнения для смеси пород
Как правило, породы осадочных свит представляют собой смесь нескольких литологических единиц (см., например, Табл. 1-3). Пористость пород, представленных такой смесью, вычисляется в соответствии с соотношением (Doligez et al., 1986), предполагающим осреднение величин обратных объёмам скелета:
(4-10)
где Ci - доля i-ой литологической единицы в породе, n – число литологических единиц в породе и ji(Z) - пористость пород i-ой литологической единицы на глубине Z. Для каждой смеси литологических единиц эффективные параметры уплотнения породы определяются в соответствие с соотношениями (4-1, 4-8, 4-10). Пример определения параметров уплотнения для смесей пород из табл. 1-3 можно увидеть в табл. 2-3.
4.1.4 Физичесие и геофизические методы определения пористости пород
В системах моделирования бассейнов значения пористости пород лежат в основе как процедуры восстановления истории погружения бассейна, так и определения термофизических параметров пород в уравнениях теплопереноса. В то же время само понятие пористости неоднозначно и определение её величины в лабораториях и полевых условмях связано с заметными трудностями. Специалисты в области механики пород различают по крайней мере четыре типа пористости вещества (Pearson, 1999): физическая или полная пористость jtotal, внутрисвязанная пористость жидкости в породах jflow, пористость течения и диффузии жидкости jdiff и, наконец, геохимическая пористость. Физическая пористость jtotal - это объём, не занятый кристаллической матрицей. Он определяется отношением объёма пустот к полному объёму породы. Она особенно важна для процедуры моделирования, так как участвует в расчётах уплотнения пород в соотношении (4-1) и в определении термофизических параметров пород (теплопроводности, теплоёмкости и теплогенерации). «Внутрисвязанная» пористость jwater, определяемая выделением воды из объёма породы и измерением её количества, всегда будет меньше полной (физической) jtotal, так как всегда остаются включения воды в мелких порах, которые не удаётся удалить высушиванием.
jwater £ jtotal
При ртутных же измерениях пористости существует другая опасность – давление, требуемое для внедрения ртути в мелкие поры, может разрушить исходную структуру глин (Pearson, 1999). Пористость течения jflow определяет скорость потока жидкости Vflow через скорость Дарси (VDarcy=-(k/m)×(dP/dx), где k – проницаемость, m - динамическая вязкость жидкости, dP/dx – градиент давления): При этом:
Vflow = VDarcy / jflow
jflow £ jwater £ jtotal
Сама скорость Дарси, как известно, есть объём жидкости, проходящий в породе в единицу времени через единицу площади пористой породы, перпендикулярной потоку, и вызванному градиентом давления dP/dx (Тёркот, Шуберт, 1985). В аргиллитах jflow будет принципиально связана с микротрещинами. Диффузионная пористость jdiff связывает диффузию в породе с диффузией в чистой воде. В глинистых породах диффузионная пористость для воды эквивалентна пористости потока, но для диффузии раствора она меньше последней. Геохимическая пористость, jgeochem, необходима, чтобы моделировать состав поровых вод и перенос реактивов в плохо проницаемых материалах, типа плотных глин. Эта пористость, по сути, является объёмом жидкости, в котором имеют место реакции. В глинистых породах она мало отличается от диффузионной пористости. Все перечисленные типы пористости удовлетворяют так называемому неравенству глин (Pearson, 1999):
jflow £ jdiff » jgeochem £ jwater £ jtota
К примеру, геохимическая пористость в аргиллитах может составлять 0.3 – 0.7 от значения jwater или jtotal. Такие неопределённости не играют большой роли в решении уравнений переноса, но важны при моделировании состава поровых вод.
В геологической практике пористость может быть оценена из скважинного каротажа. Как известно, звуковой каротаж это запись времени, необходимого для прохождения волнами сжатия, излучаемыми прибором, одного фута (30.48 см) формации до приёмника. Это время обратно пропорционально скорости волн, которая является функцией литологии пород и пористости. При известной литологии пористость может быть определена из соотношения:
Dt = Dtma ×(1 - j) + j×(Dtf) (4-11)
где Dtma есть время прохождения звука через твёрдую матрицу пород (51.3 – 55.5 mсек (10-6 сек) / фут для песчаников и 43.5 – 47.6 mсек / фут для известняков). Время прохождения сигнала через поровую жидкость (Dtf) зависит от солёности вод и для пресного флюида составляет 189 mсек / фут.
Плотность пород при известной литологии также может дать оценку пористости пород, так как для плотности справедливо соотношение аналогичное (4-11):
r = rma ×(1 - j) + j×(rf) (4-12)
где rma – плотность твёрдой матрицы пород и rf – плотность поровой жидкости. Для определения плотности проводят плотностной каротаж (гамма-каротаж). Гамма лучи из источника рассеиваются на электронах в породе формации, давая информацию о плотности электронного облака и вместе с ней и о плотности породы. Однако, для эвапоритовых пород (соль, сильвинит (KCl)) и угля различие в значениях реальных плотностей и измеренных этим методом существенны, и сам метод неточен. Присутствие остаточного газа в порах также может искажать результаты анализа.
Применение нейтронного каротажа для оценки пористости пород основано на том, что нейтроны, излучаемые источником, захватываются ядрами формации. Детектор подсчитывает не поглощённые нейтроны. Нейтронный каротаж даёт меру содержания воды в породе. Большие ошибки при оценках пористости таким методом могут вноситься присутствием глинистых минералов, содержащих связанную воду.
Из всех перечисленных видов звуковой каротаж используется наиболее часто.
4.1.5 Оценки объёма неуплотнённых осадков
Выше отмечалось, что в процедуре численного моделировании бассейнов процесс формирования осадочной толщи воспроизводится последовательным отложением тонких слоёв неуплотнённых осадков Dz1 на поверхности бассейна (Рис. 1-4). Поэтому оценки необходимого объёма неуплотнённых осадков являются составной частью моделирования. При отложении элементарного слоя на поверхности, породы, лежащие ниже, уплотняются. Применяя соотношение (4-1) к мощности слоя, лежащего на глубинах z1 £ z £ z2 в современном разрезе, получаем объём неуплотнённыx литологически однородных осадков Н0, который необходимо отложить дискретными порциями Dz1 на поверхности бассейна, чтобы в итоге с учётом уплотнения получить наблюдаемую в современном разрезе толщу:
(4-13)
Для экспоненциального закона (4-3) отсюда получаем:
(4-14)
Соответствующее значение H0 для линейной зависимости (4) имеет вид:
для Z1, Z2 £ B
для Z1 £ B но B £ Z2 (4-15)
для Z1, Z2 ³ B
Объём неуплотнённых осадков вычисляется в системах моделировании по формулам (4-13) – (4-15) с поправками на возможное влияние эрозии части слоя, одного или нескольких слоёв. При сложной истории развития бассейна этот объём корректируется в итерационном режиме, чтобы приблизить вычисленный современный разрез к наблюдаемому в бассейне. Из (4-13) – ((4-15) видно, что объём неуплотнённых осадков связан с мощностью слоя (z2 – z1) на больших глубинах, где пористость пород близка к нулю, предельным соотношением:
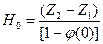(4-16)
Из него и табл. 1-4 следует, что в зависимости от начальной пористости осадков значение Ho может в 2-3 раза превосходить мощность слоя в современном разрезе. Процесс уменьшения толщины слоя по мере его погружения в бассейне можно увидеть и на рис. 1-3б на примере осадочных толщ разреза площади Такхухт Восточно-Алжирского бассейна, сравнивая современные мощности слоёв с их толщинами на время окончания процесса отложения слоя на поверхности. Так согласно моделированию и табл. 2-3 объём неуплотнённых пород кембрия-ордовика, который необходимо было отложить при моделировании на поверхности, составлял Ho » 730 м, что почти в два раза превосходило мощность этого слоя в современном разрезе (DH = 400 м; Рис. 3-1). Для нефтематеринской пачки силура соответствующие значения объёмов неуплотнённых и уплотнённых пород составляли Ho » 123 м и DH = 70 м. Отметим, что объём неуплотнённых осадков Ho и интервал времени ti1 £ t £ ti2 их отложения на поверхности бассейна определяют среднюю скорость отложения осадков при формировании слоя: Hoi / (ti2 - ti1).