Диаграмме деформирования
Пусть мы имеем некоторую диаграмму деформирования (рисунок - 2).
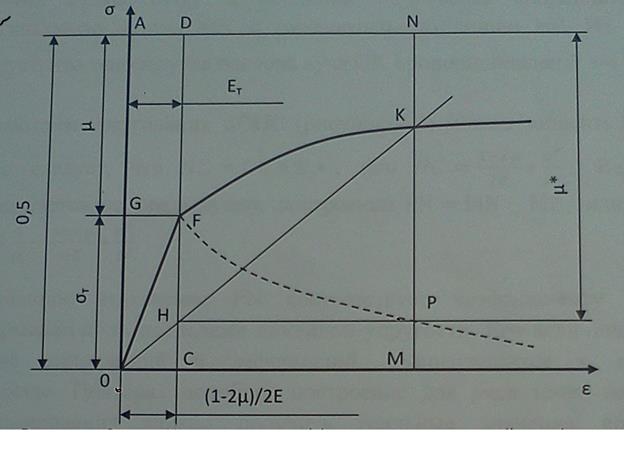
Рисунок 2 - Изменение коэффициента поперечной деформации (пунктирная линия) в зависимости от величины деформации
Для получение коэффициента поперечное деформации по оси абсцисс введем новый масштаб 
где µ - коэффициент Пуассона;
Е - модуль упругости.
Из OАВ следует, что tan а = 
= Е или АВ = ОG = ОВ * Е = 
Таким образом, по оси ординат масштаб напряжения ОG = 
изменен и теперь соответствует величине АВ=OG= 
Зная новый масштаб по оси ординат, отложим отрезок OA, соответствующий величине ОА=0,5. В этом случае отрезок AG будет соответствовать величине µ.
На диаграмме деформирования (рисунок - 2) возьмем некоторую точку К(σ*,ε*) за пределами линейной упругости и установим для величины деформации ε*, определяемой этой точкой, коэффициент поперечной деформации.
С этой целью точку К соединим с началом координат, проведем -вертикальную линию MN и горизонтальную линию HP. Из построения следует, что тангенс угла наклона луча ОК пропорционален Е*= 
.
Рассмотрим треугольник АОНС (рисунок - 2) можем записать Е *= 
.
Из этого следует, что НС = 
, или НС = 
. Величина PN определяется из предыдущих построений PN = MN — MP, или
PN = OA — НС =
Полученное выражение PN соответствует коэффициенту поперечной деформации //* за пределами линейной упругости. Его величина зависит от уровня напряжений и деформаций, реализующихся в исследуемом материале. Повторяя подобное построение для ряда точек на диаграмме деформирования можно получить реальные значения коэффициента поперечной деформации, в виде графика GFP
(рисунок - 2)
Определение коэффициента поперечной деформации по диаграмме
Деформирования для сплава Ст 18 ХНВА
В соответствии с пунктом 4, выполним необходимые построения и определим графическое значение коэффициента поперечной деформации 
в 6 произвольных точках лежащих за пределами линейной упругости:
Для этого примем отрезок OL=0,5, а длину от линии LM до пересечения с точками F|, К|,…,K4| за х, тогда получим:
: 123,2=0,5
107,3=х →
→ 
Аналогично находим значения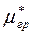 
для остальных точек, получим:
0,4354;
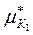=0,4248;
=0,4088;
=0,3832;
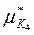=0,3517;
=0,3000.
Определим расчетное значение коэффициента поперечной деформации 
по формуле:
, где 
=0,3 – Коэффициент Пуассона;
Е – модуль упругости;
и 
– напряжение и деформация в
соответствующей точке.
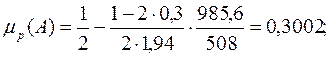
Все полученные данные сносим в таблицу 2:
Таблица 2 – Обобщенные данные.
| точка |
|
|
| 
|
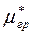
| F | 0,4410 | 0,4410 | ||
| K | 1127,2 | 0,4354 | 0,4355 | |
| K1 | 1094,4 | 0,4248 | 0,4249 | |
| K2 | 1061,4 | 0,4088 | 0,4089 | |
| K3 | 1028,6 | 0,3822 | 0,3824 | |
| K4 | 1006,8 | 0,3517 | 0,3519 | |
| А | 985,6 | 0,3000 | 0,3002 |
Оценка точности. Расчет погрешности вычислений
Произведем расчет погрешности найденных коэффициентов и 
по формуле:
, где 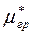- графическое значение коэффициента
деформации;
- расчетное значение коэффициента
деформации.
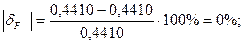
Все полученные данные занесем в таблицу 3:
Таблица 3 – Погрешность расчетов.
| точка |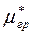
|
|  ,%
|
| F | 0,4410 | 0,4410 | |
| K | 0,4354 | 0,4355 | 0,022 |
| K1 | 0,4248 | 0,4249 | 0,023 |
| K2 | 0,4088 | 0,4089 | 0,024 |
| K3 | 0,3822 | 0,3824 | 0,052 |
| K4 | 0,3517 | 0,3519 | 0,057 |
| K5 | 0,3000 | 0,3002 | 0,066 |
Вывод
Исходя из диаграммы деформирования стали, коэффициент поперечной деформации зависит от уровня напряжений и деформаций, реализующиеся в исследуемом материале.
С увеличением напряжений и деформаций увеличивается коэффициент поперечной деформации и в* некотором значении он достигнет 0,5.
Графический расчет отражает теоретическое представление коэффициента поперечной деформации с погрешностью не превышающей 1%