Формулировка и некоторые свойства решений задачи коммивояжера

Основные понятия теории графов

Геометрически граф можно представить как набор вершин, определенные пары которых соединены линиями. Например, сеть дорог, соединяющих автобусные остановки , , , , 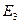, можно представить в виде графа следующим образом. Автобусные остановки обозначены точками (вершинами), а дороги – неориентированными линиями (Рис.1).

Рис. 1

Неориентированные линии означают наличие двустороннего движения между соответствующей парой остановок. Пересечения линий не считаются вершинами.

При изображении графа не имеет значение расположение вершин на плоскости, кривизна и длина ребер (Рис. 2).

Рис. 2

Вершины графов обозначаются буквами или натуральными числами. Ребра графа – пары чисел.

Графические представления – наглядные отображения исследуемой системы процесса или явления на плоскость: рисунки, чертежи, схемы и блок-схемы, диаграммы, графы. На языке теории графов формируются и решаются многие технические задачи, задачи из области экономики, социологии, менеджмента и т.д. Графы используются для наглядного представления объектов и связи между ними.

Маршрутом в G называется такая конечная или бесконечная последовательность ребер, что каждые два соседних ребра имеют концевую точку. Причем, одно и то же ребро Е может встречаться в маршруте несколько раз.

Циклическим маршрутом называется такой маршрут, начальная и конечная точки которого совпадают.

Цепью называют маршрут, в котором каждое его ребро встречается не более одного раза; вершины в цепи могут повторяться не более одного раза. Любой участок цепи является цепью.

Нециклическая цепь является простой цепью, если в ней никакая вершина не повторяется.

Пусть задано некоторое непустое Х множество, состоящее из пар элементов множества X. Пары во множестве могут повторяться, и также могут повторяться элементы в парах. Множества Х задают граф 0=(Х, Y).

Элементы множества называют вершинами графа, элементы множества V — ребрами графа.

Если пары во множестве V повторяются, то граф С называют псевдографом или графом с кратными ребрами.

Если элементы в парах множества не упорядочены, то граф С называют неориентированным графом. Если они упорядочены, то граф О является ориентированным графом или орграфом, а эле­менты множества V называют дугами.

Графически граф задается в виде точек и линий, их соединяющих.

Введем ряд основных понятий для неориентированного графа. Ребро, начало и конец которого совпадают, называется петлей. Вершины называются смежными или соседними, если суще­ствует ребро, их соединяющее.

Если вершина является началом или концом ребра, то верши­на и ребро называются инцидентными.

Степенью вершины называется число инцидентных ей ребер. Вершина, степень которой равна нулю, называется изолированной. Вершина, степень кото­рой равна единице, называется висячей или тупиковой.

Маршрутом в графе называется последовательность вершин и ребер, в которой конец предыдущего ребра совпадает с началом следующего, это не относится к первому и последнему ребру. Число ребер в маршруте определяет его длину.

Цепью называется маршрут, в котором все ребра попарно раз­личны.

Простой называется цепь, в которой все вершины попарно различны.

Циклом (простым циклом) называется цепь (простая цепь), начало и конец которой совпадают.

Граф называется связным, если для любых двух его вершин существует цепь, соединяющая эти вершины.

Расстоянием между вершинами связного графа называется длина самой короткой цепи, соединяющей вершины.

Диаметром графа называется максимальное расстояние между его вершинами.

Деревом называется связный граф без циклов

Граф называется регулярным степени i, если все его вершины имеют

степень i.

Граф называется полным, если любые две его вершины соеди­нены ребром. Лесом называется граф без циклов, т.е. совокупность деревьев.

Регулярный граф, все вершины которого имеют степень 1, на­зывается паросочетанием. Граф называется двудольным, если мно­жество его вершин X может быть разделено на два непересекаю­щихся подмножества таким образом, что каждое ребро графа соединяет вершины из двух разных подмножеств.

Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.

Гамильтоновым циклом называется простой цикл, содержащий все вершины графа.

В ориентированном графе каждая дуга имеет направление, показанное стрелкой

Маршрут в ориентированном графе часто называют контуром, а цепь — путем.

Формулировка и некоторые свойства решений задачи коммивояжера

Классическая постановка задачи о коммивояжере выглядит следующим образом:

Имеется N городов, выезжая из исходного города А1, коммивояжер должен побывать во всех городах по 1 разу и вернуться в город А1. Задача заключается в определении последовательности объезда городов, при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время пути, суммарное расстояние и т.д.

Для расчета затрат существует матрица условий, содержащая затраты на переход из каждого города в каждый, при этом считается, что можно перейти из любого города в любой, кроме того же самого (в матрице как бы вычеркивается диагональ). Целью решения является нахождения маршрута, удовлетворяющего всем условиям и при этом имеющего минимальную сумму затрат.

Чтобы привести задачу к научному виду, введём некоторые термины. Итак, города перенумерованы числами jÎТ=(1,2,3..n). Тур коммивояжера может быть описан циклической перестановкой t=(j₁,j₂,..,j_n,j₁), причём все j₁..j_n – разные номера; повторяющийся в начале и в конце j₁, показывает, что перестановка зациклена. Расстояния между парами вершин С_ij образуют матрицу С. Задача состоит в том, чтобы найти такой тур t, чтобы минимизировать функционал

Относительно математизированной формулировки задачи коммивояжера

уместно сделать два замечания.

Во-первых, в постановке С_ij означали расстояния, поэтому они должны быть неотрицательными, т.е. для всех jÎТ:

С_ij³0; C_jj=∞

(последнее равенство означает запрет на петли в туре), симметричными, т.е. для всех i,j:

С_ij= С_ji.

и удовлетворять неравенству треугольника, т.е. для всех:

С_ij+ С_jk³C_ik