1.1. Определения теории информации
Понятие «информация» широко используется человеком. Это следует из того, что физические явления, воздействующие на человека, рассматриваются им как информация, получаемая от внешних источников. При оценке какого-либо события или для принятия решения человек преобразует (перерабатывает) информацию. Аналогичные процессы происходят в системах обработки данных, но, естественно, по более упрощенному сценарию.
В теории информации основным понятием является понятие информационного процесса или информации. Для раскрытия их содержания проследим возникновение информационных представлений на примере взаимодействия двух физических элементов – А и В. В результате взаимодействия элемент А создает на элементе В какие-либо изменения, т.е. у элемента В появляются новые свойства. Предположим, что свойства элемента В могут быть оценены элементом В или некоторым элементом С, которые является получателем информации. Условимся новые свойства элемента В называть информацией, полученной элементом В от элемента А, если элемент В может их оценить. Если же оценку новых свойств элемента В осуществляет третий элемент С, то будем говорить, что элемент С получает информацию от элемента В.
Развивая рассмотренные представления, выделим основные свойства информации:
1. Понятие информации всегда связано с понятием физического процесса.
2. Информация, как всякое физическое явление, имеет не одно, а большое количество независимых свойств.
3. Физическая модель информации основана на том, что информация, содержащаяся в физическом процессе, всегда связана с оценкой одного из его свойств человеком или ЭВМ / системой. Другими словами, информационный процесс – это не всякий физический процесс, а лишь тот, хотя бы одному из свойств которого дается человеко-машинная оценка.
|
|
Исходя из этого, информацию будем рассматривать как физический процесс, одно из свойств которого оценивается человеком или ЭВМ. Отсюда следует: важно знать на кого физические процессы воздействуют и кто проводит их оценку.
1.2. Характерные черты и некоторые свойства информации
Информационный процесс имеет неограниченное число различных свойств, к которым применяют оценки, причем различные для каждого свойства. Поэтому в теории информации должна рассматриваться не одна какая-либо оценка, характеризующая лишь одно из свойств, а все равноправные независимые оценки, используемые в инженерных науках. Например, свойства процесса могут оцениваться каким-либо моментом функции распределения или энтропией или используются минимаксные оценки.
Такое расширенное понимание теории информации позволяет решать широкий круг инженерных задач на основе общеинформационных представлений.
Таким образом, одну информацию можно оценивать по-разному, давая ей различные оценки. Заметим, что результаты оценки какого-либо свойства информационного процесса можно преобразовать в новый информационный процесс с новой оценкой. Например, первой оценкой какого-либо свойства процесса может быть измерение, т.е. оценка свойства по алгоритму отношения. Можно провести оценку полученных результатов с использованием нового алгоритма, например, оценка достаточности объема измерений. Здесь оценкой является выход измеренной величины за допуск.
|
|
Иногда вводят «новые информации», отличные от энтропийной меры и называемые семантической информацией. Но это – плата за стремление характеризовать большое число разных свойств информационного процесса какой-то одной оценкой.
Другим важным понятием информационных процессов и систем являются их характеристики. Суть здесь в следующем. Каждое свойство информационного процесса стремятся описывать своей характеристикой относительно используемой оценки. Соответственной характеристикой должна описываться и информационная система. Например, динамические характеристики будут рассматриваться как характеристики по отношению к амплитудно-временной оценке. По отношению к энтропийной оценке характеристиками являются пропускные способности системы.
Возникновение новой информации может быть обусловлено появлением новых свойств у процесса, которые ранее не замечали, и введением новых оценок, например, за счет появления новых гармоник в исследуемом процессе.
Приведенные свойства показывают, что информация существует лишь для получателей, имеющих некоторую оценку. Информационное рассмотрение физического процесса не исключает его одновременного рассмотрения и с других позиций, например, с энергетической. В любом случае существуют простые оценки процесса, принимаемые за физические или математические меры. Комбинируя их, получаем алгоритмы, которые и назовем оценками.
1.3. Дискретная и непрерывная информация
Информационные процессы могут иметь дискретную и непрерывную физическую и математическую модели. Разговор человека – это одновременно как дискретная, так и непрерывная информация. Дискретность и непрерывность – некоторая идеализация и математически удобное представление информации.
|
|
Для передачи информации, заданной в непрерывной форме, необходимо представить ее в дискретной форме. Для этого проводят дискретизацию по аргументу и по амплитуде. Дискретизация по аргументу сводится к представлению непрерывной функции в виде импульсов во времени, шириной которых ∆τ можно варьировать (рис. 1.1,а), т.е. к формированию разрывной функции.
Часто применяется дискретизация при ∆τ → 0. Дискретизация по амплитуде или квантование означает создание ступенчатости функции по оси ординат.
Рассмотрим представление непрерывной функции f(t) в дискретной форме. Для этого по оси t выбираем интервал дискретизации ∆t и ширину импульса ∆τ (рис. 1.1,б), затем по выбранной величине кванта ∆f проводим квантование функции f(t) (рис. 1.1,г). Совмещая дискретизацию по аргументу и по амплитуде, получим дискретную функцию, приведенную на рис. 1.1,д. Если ширина импульса ∆τ → 0 (0 < ∆τ < ∆t), имеем процесс дискретизации, показанный на рис. 1.1,е.
Дискретизация функции по оси времени проводится на основании теоремы Котельникова. В этом случае ∆t = ½ ωС, где ωС – наивысшая частота в спектре рассматриваемой функции.
Интервал квантования по уровню выбирается из условия ∆f = 2 Emax, где Emax – величина максимально возможной ошибки, возникающей при передаче сигнала f(t). Для преобразования дискретной информации в непрерывную используются различные методы аппроксимации.
Рис. 1.1. Преобразование непрерывной информации в дискретную при интервале дискретизации по аргументу ∆t и шаге квантования ∆f.
1.4. Теорема Котельникова
Данная теорема позволяет установить взаимосвязь между непрерывным и дискретным представлением функций. Она находит широкое применение при представлении непрерывной функции ее дискретными значениями, а также при определении необходимого количества точек при экспериментальных исследованиях, в задачах сглаживания информации и других задачах. Существо теоремы Котельникова состоит в том, что непрерывная функция f(x), имеющая конечный спектр, представляется в виде ряда, в котором используются функции отсчета в виде Sin x/x. График этой функции отсчета приведен на рис. 1.2.
Рис. 1.2. Функция отсчетов.
Рассмотрим основные свойства функции:
1. Значение функции отсчета в нулевой точке, как известно из теории пределов, равно единице, т.е.
2. Значения функции в точках x = πn, где n = ±1, ±2, …, равны нулю в силу того, что в этих точках Sin x = Sin πn = 0.
3. Амплитуда функции отсчета быстрозатухающая в силу быстрого возрастания знаменателя и ограниченного изменения числителя.
4. Для функции отсчета вида 
преобразование Фурье
представляет собой прямоугольный импульс, высота которого равна единице на интервале 
.
5. Площадь, ограничиваемая функцией отсчета, равна единице:
Доказательство теоремы Котельникова приведено в работе [4]. Математическим выражением этой теоремы является соотношение:
где 
– произвольная непрерывная функция;
интервал дискретизации.
Теорема Котельникова формулируется следующим образом: если функция не содержит гармоник, превышающих 
Гц, то она может быть представлена ее значениями в точках отсчета, находящихся друг от друга на расстоянии:
.
Теорема Котельникова интерпретируется как сумма функций отсчета, построенных в точках отсчета с интервалом 
. Амплитуда этих функций равна значениям функции 
в точках отсчета, т. е. 
, 
, 
. Теорема легко обобщается на случай несимметричного относительно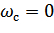 
спектра. Временной интервал при этом определяется как 
. В инженерной практике часто используются функции, ограниченные во времени. Спектр для таких функций оказывается неограниченным. Таким образом, применение этой теоремы для функций, ограниченных во времени, сопряжено с ошибкой аппроксимации.
Чтобы уменьшить ошибку, интервал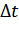 
берут малым, а это означает, что должна возрастать . Данные ограничения, свойственные теореме Котельникова, являются примером проявления соотношения неопределенности, имеющего место в информационных процессах.
1.5. Понятие о кодировании.
Понятие кодирования обычно связано с понятием дискретной информации, хотя оно может быть развито для непрерывной информации. В его основе лежит проблема «языка» как одна из основных проблем теории информации, поскольку наличие «языка» обязательно для передачи информации от объекта к объекту.
Дискретные языки назовем кодом. Бывает и непрерывный язык, например, модуляцию рассматривают как непрерывный язык. Под кодированием будем понимать отображение одного дискретного явления на другое дискретное. Действительно, дискретная информация всегда представлена в виде набора определенных символов, например, цифр, которые ее характеризуют. Конечное множество различных символов называют кодовым алфавитом, а отдельный символ называется элементом или буквой. С позиций «языка» различные его элементы являются элементами алфавита или кода.
Часто используется алфавит, состоящий из небольшого числа различных букв (например, в двоичном коде имеются две различные буквы (0,1)). Для того, чтобы, используя двоичный код, выразить 32 различные буквы русского алфавита, создают кодовые слова, которые имеют одинаковое или различное число букв. В первом случае код называется равномерным. Его примером является двоичный пятизначный код Бодо. Примером неравномерного кода служит код Морзе, в котором алфавит состоит из двух букв: точки и тире, а кодовые слова имеют различную длину. Таким образом, в понятие кода могут включаться определенные комбинации из букв алфавита в виде кодовых слов.
Число букв алфавита «b» называется основанием кода. Каждой букве алфавита сопоставляется элементарный сигнал. Например, в двоичном коде «буквам алфавита» 0 и 1 соответствует пауза и посылка тока определенной длительности, т.е. ступенчатое представление кода. Число букв в кодовом слове называется его длиной n, значностью или разрядностью. Например, код Бодо, имеющий пять букв в кодовом слове, является двоичным пятизначным кодом. Максимальное число различных сочетаний букв в двоичном коде Бодо равно N = bn = 25 = 32, а в двоичном десятизначном коде N = bn = 210 = 1024.
Рассмотренные примеры показывают, что простейшее кодирование есть отображение элементов одного конечного множества с помощью элементов другого конечного множества. От выбранного кода зависит количество преобразуемой и передаваемой информации, ее достоверность.
Информация, представленная в непрерывной форме, также всегда закодирована. Например, функция C(t), описывающая изменение концентрации метана в исходящей вентиляционной струе во времени, обычно имеет линейно-амплитудное кодирование в реальном времени. Эту функцию можно преобразовать, например, преобразовать аргумент путем изменения масштаба или введением неравномерного масштаба, то есть перекодированием непрерывной информации.
В соответствии с принятыми физическими представлениями об информации можно определиться с понятием «сигнал», под которым будем понимать всякий пространственно-временной информационный процесс с любым кодом. Если к сигналу применяются какие-либо преобразования, то будем их понимать как преобразования амплитудно-временных свойств процесса вне зависимости от букв кода.
Информация, содержащаяся в исследуемом процессе, часто представлена в амплитудно-временном коде. В случае дискретной информации говорят, что информация имеет амплитудно-импульсный код, в случае непрерывного сигнала – непрерывный амплитудно-временной код.
При использовании амплитудно-временного кода, как и для других кодов, для исследуемой информации применимы разные оценки. Например, оценивается максимальная величина амплитуды, или определяется величина отклонения данного процесса от какого-то другого (при сравнении входного и выходного сигналов). В других случаях интересует величина квадрата амплитуды, например, при определении мощности сигнала, или оценивается скорость изменения амплитуды и т.д. В частности, при рассмотрении основных задач детерминированного сигнала для информационной системы исследуются амплитудно-временные зависимости между сигналами и характеристики системы, определяющие данные зависимости. При этом полагается, что возможно применение разных оценок по отношению к амплитудно-временным соотношениям.
1.6. Информационные аспекты построения систем
Прежде всего, уясним ряд особенностей, связанных с понятием «информация». Массовое внедрение ЭВМ в различные сферы жизни общества привели к изменениям в трактовке информации:
1. Включен обмен информацией между человеком и ЭВМ, между ЭВМ и ЭВМ, обмен сигналами в животном и растительном мире, т.к. вся генетика построена на информационных признаках.
2. Предложена количественная мера информации, что привело к созданию информационной теории (работы К.Шеннона, Дж.Хартли, А.Н.Колмогорова).
И. И. Юзвишин ввел основные законы информациологии и утверждал их превосходство над другими философскими категориями, в том числе и над материей.
При информационном анализе надо оценить как информационную структуру, так и ее функции, т.е. установить взаимосвязь объектов и процессов (рис.1.3).
| Объекты |
| Уровень |
| Структурная информация |
| Процессы |
| Темп |
| Оперативная информация |
Рис. 1.3. Взаимосвязь процессов и объектов.
Взаимосвязь потоков информации с материей (структурами) приводит к понятию отражения, т.е. свойству материи фиксировать и сохранять в своей структуре следы воздействия другой системы. Отражение – одно из свойств материи (пространство, время, движение), причем оно развивается вместе с развитием материи. По А.Урсулу, информация – отраженное разнообразие реального мира, и чем разнообразнее система, тем более адекватно она отражает мир. Составляющие информации представлены на рис 1.4.
| МАТЕРИЯ |
| ОТРАЖЕНИЕ |
| Информация |
| Физическая |
| Биологическая |
| Социальная |
Рис. 1.4. Составляющие информации.
Физическая – отражается в движении материи (механическом, физическом, химическом и т.д.) Биологическая информация включает генетику, физиологию, психологию и мышление человека. Социальная, обычно представляемая в форме научного прогнозирования, делится на две группы:
- массовую информацию, обеспечивающую функции общения;
- специальную информацию, обеспечивающую функции созидания (научную, техническую и т.д.) и переходящую в новые структуры, предназначенные для повышения эффективности информационных технологий (базы знаний, искусственный интеллект).
На практике приходится сталкиваться с интегральным потоком информации, в котором присутствуют все указанные составляющие, которые реализуются в виде материальных носителей информации во времени и пространстве – сигналов. Они подразделяются на сигналы воздействия среды; сигналы, реализующие априорную информацию (овеществленные знания в виде результатов НИОКР, патенты, человеческий опыт и т.д.) и сигналы управления (команды ЭВМ, директивы лица принимающего решения (ЛПР) и т.д.)
Оперативная информация делится на:
- атрибутивную – тип сигнала, время поступления, вид контроля;
- адресную – места поступления и назначения;
- количественную – значения параметров, факторов;
- управленческую – известительную и распорядительную.
Основными характеристиками оперативной информации являются: достоверность (безошибочность); своевременность (время переработки информации соответствует динамике процесса); старение (рассогласованность показателей во времени); безопасность (невозможность изменения данных).
Рассмотрим особенности материального носителя информации – сигнала и виды представления информации в ЭВМ. В качестве сигнала выступает не сам объект, а его состояние. На диски можно записывать различные файлы, не меняя основной функции хранения информации. Далеко не всякое состояние имеет сигнальные свойства, так как сигнал может быть забит помехами или шумами, может произойти рассогласование кодов взаимодействующих объектов. Сигналы могут быть статические: книга, фотография и т.д.; динамические, зависящие от состояния силовых полей: свет, звук, радиосигнал и т.п. Поскольку сигнал – состояние физического объекта, то математической моделью этого состояния будет являться случайный процесс, дающий вероятностное представление о поведении сигнала во времени. Процессы могут быть:
- непрерывные;
- дискретные (случайная последовательность сигналов);
- стационарные в узком и широком смысле;
- нестационарные.
Сигналы в модели могут представлять собой:
- гармонический сигнал
X (t) = A (cos ωt + φ),
где А – амплитуда, ω = 2πf – круговая частота; φ – фаза;
- модулированный по амплитуде, частоте или фазе периодический сигнал:
Х (t) = X (t + τ);
- импульсный сигнал
Х (t) = 0, t 
T.
Помехи чаще всего представляются в виде стационарного нормального случайного процесса. Превращение информации в ресурс ставит вопрос её накопления, хранения и переработки. Современный производственный процесс порождает огромное количество информации на различных носителях: на бумажных (записи в рабочих журналах, бланки, рекламации и т.д.) и машинных. Возникает двойственная картина: с одной стороны, информации много, с другой – ее не хватает для принятия решения. Можно утверждать, что накопление пассивной неструктурированной информации является одним из новых видов загрязнения среды. Стремление упорядочить потоки оперативной информации, свернуть ее, обеспечить достоверность и своевременность привело к методам организации информационных массивов так, чтобы они послужили основой безбумажного обмена в рамках используемой информационной технологии. Сейчас есть возможность перерабатывать информацию в символьной форме. Представление априорной информации и результатов исследовательской деятельности в формализованном виде, пригодном для накопления, обработки и передачи средствами вычислительной техники, назовем данными.
В человеко-машинной системе данные за счет интеллектуальных возможностей человека приводят к получению новой информации, представляющей из себя знания.
Любая человеко-машинная система принятия решений включает в себя развитые банки знаний и базы данных, корректируемые по мере получения новых данных или знаний.
Одной из главных задач при исследовании и создании систем, в том числе систем искусственного интеллекта, является оценка их информационных свойств и структурных компонент. Эта задача достаточно сложна из-за необходимости учета как качественных, так и количественных характеристик информации. Причем, в большинстве случаев приходится решать задачу извлечения полезной для исследования информации из общего объема имеющейся в наличии, а также задачу преобразования информации. Становлению теории информации как науки способствовали работы К.Шеннона, А.Н.Колмогорова, В.А.Котельникова, Дж.Хартли и других. В этих работах подчеркивается, что центральной задачей теории информации является изучение её преобразований. Выделим следующие основные виды преобразований:
1) преобразование физической природы информационного процесса, например, информационный процесс в виде термодинамического газового процесса, в котором оценивается его давление, преобразуется датчиком давления в аналогичный процесс изменения электрического напряжения; при этом информация не меняется, а лишь изменилась физика процесса;
2) преобразование кода информационного процесса, называемое кодированием или декодированием, например, текст телеграммы перекодировали в двоичный код, при этом существо осталось прежним, а буквы стали другими;
3) преобразование информации за счет изменения свойств информационного процесса при сохранении кода и оценки, например, взаимодействие двух информационных процессов с формированием новой информации на прежнем языке.
На рис.1.5 приведена структурная схема простейшей информационной системы, на которой дана информационная интерпретация ее элементов как преобразователей информации: 1 – источник информации; 2 – датчик, преобразующий физическую природу процесса из одной формы в другую; 3 – преобразователи кода, в качестве которых могут быть модулятор (кодирующее устройство), переводящий амплитудно-временной язык в другой язык, и декодирующее устройство (демодулятор), которое с языка, удобного для передачи информации, переводит информационный процесс в амплитудно-временной язык; 4 – преобразователь нескольких информационных процессов в соответствии с заданным алгоритмом преобразования на амплитудно-временном языке; 5 – устройство, предназначенное для оценки информации.
Рис.1.5. Структурная схема простейшей информационной системы.
Развитые в данном разделе представления позволяют теорию информации определить как теорию, с помощью которой изучаются информационные процессы, системы и их взаимодействие.
Контрольные вопросы
1. Дайте определение понятия информационная технология.
2. Охарактеризуйте взаимодействие потоков информации и структур.
3. Дайте определения понятиям информация и теория информации.
4. Характерные черты и основные свойства информации.
5. Что такое дискретность и непрерывность информации?
6. Как происходит преобразование непрерывной информации в дискретную при интервале дискретизации по времени ∆t и шаге квантования ∆f?
7. Что называется оценкой информационного процесса?
8. Как формулируется теорема Котельникова? Каков ее содержательный смысл?
9. Перечислите свойства функции отсчетов. Назовите ограничения, свойственные теореме Котельникова.
10. Поясните понятие кодирования информации. Что называется кодом?
11. Как осуществляется процесс кодирования?
12. Какая связь между информацией и отражением?
13. Назовите составляющие информации.