Лабораторная работа № 4
Тема: «Модели и методы стохастического программирования»
Постановка задачи.................................................................................................................................................. 1
Варианты.................................................................................................................................................................... 3
Форма отчета............................................................................................................................................................ 7
Контрольные вопросы............................................................................................................................................ 8
Пример 1..................................................................................................................................................................... 9
Пример 2................................................................................................................................................................... 10
Пример 3................................................................................................................................................................... 12
Пример 4................................................................................................................................................................... 14
Примеры постановок задач стохастического программирования с Р-ограничениями..................... 15
Дополнительные задания. Стохастическая ТЗ (Юдин 35)........................................................................ 17
Список рекомендуемой литературы и интернет-ссылок............................................................................ 18
Цель: освоение постановок, моделей, методов и принципов оптимизации в условиях стохастической неопределенности, а также инструментальных средств для решения задач стохастического программирования.
Задачи:
- Изучить основные постановки задач стохастического программирования
- уяснить разницу между видами решений (детерминированное, решающее правило, *решающее распределение) задач стохастического программирования
- освоить подходы к построению детерминированных эквивалентов основных постановок задач стохастического программирования
- овладеть инструментальными средствами решения и анализа задач стохастического программирования.
Постановка задачи
Дана порождающая ЗЛП
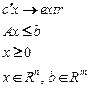
Для заданной порождающей ЗЛП при 
· составить задачу стохастического программирования (ЗСтП) (постановка согласно варианту),
· построить ее детерминированный эквивалент (тип решения - согласно варианту),
· графически изобразить множество планов детерминированного эквивалента и линии уровня ее целевой функции,
· решить детерминированный эквивалент с помощью программных средств, дать интерпретацию полученного результата.
· Построить детерминированный эквивалент для этой же задачи с целевой функцией и ограничениями в М-постановках, графически изобразить множество планов детерминированного эквивалента и линии уровня ее целевой функции, решить детерминированный эквивалент с помощью программных средств, дать интерпретацию полученного результата.
· Сравнить решения в разных постановках. Сделать выводы.
· исследовать вид множества планов детерминированного эквивалента при различных значениях  -уровня
-уровня
· Исследовать зависимость решения от  -уровня (от 0.5 до 0.9 с шагом 0.05)
-уровня (от 0.5 до 0.9 с шагом 0.05)
· При каких значениях  оптимальное решение не меняется?
оптимальное решение не меняется?
· изучить распределение целевой функции на найденном оптимальном решении
· * проверить условие доминирования ограничений (в стохастической постановке)
Недостающие параметры условия задать самостоятельно.
Варианты
В1 А - детерминированная матрица  ,
,  - случайный вектор с заданными плотностями вероятностей компонент:
- случайный вектор с заданными плотностями вероятностей компонент: 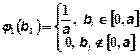 ,
,  ,
,  с - случайный вектор с известными математическими ожиданиями компонент:
с - случайный вектор с известными математическими ожиданиями компонент:  .
. 
ЗСтП с целевой функцией в M-постановке и ограничениями в Р-постановке. Решение - детерминированный вектор.
В2 Компоненты матрицы А и вектора  - независимые нормально распределенные случайные величины с заданными математическими ожиданиями
- независимые нормально распределенные случайные величины с заданными математическими ожиданиями  ,
, 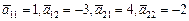 ,
, 
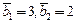 , и дисперсиями
, и дисперсиями 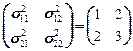 ,
,  , с - детерминированный вектор,
, с - детерминированный вектор, 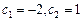 .
.
ЗСтП с ограничениями в Р-постановке. Решение - детерминированный вектор.
В3 А - детерминированная матрица  ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями 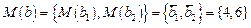
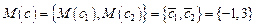 и дисперсиями
и дисперсиями 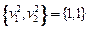 ,
, 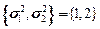 . ЗСтП с целевой функцией на максимум в V-постановке и ограничениями в M-постановке. Решения в виде линейных решающих правил.
. ЗСтП с целевой функцией на максимум в V-постановке и ограничениями в M-постановке. Решения в виде линейных решающих правил.
В4 А - детерминированная матрица 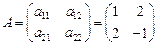 ,
,  - случайный вектор с заданными плотностями вероятностей компонент
- случайный вектор с заданными плотностями вероятностей компонент 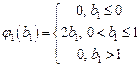 ,
, 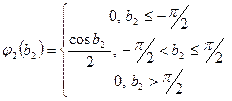 , с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями
, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями 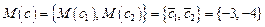 и ковариационной матрицей
и ковариационной матрицей 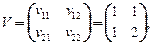 . ЗСтП с целевой функцией в К-постановке и ограничениями в Р-постановке. Решение - детерминированный вектор.
. ЗСтП с целевой функцией в К-постановке и ограничениями в Р-постановке. Решение - детерминированный вектор.
В5
А - детерминированная матрица 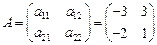 ,
,  - случайный вектор с заданными плотностями вероятностей компонент
- случайный вектор с заданными плотностями вероятностей компонент  ,
, 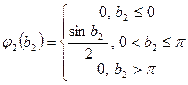 ,
,
с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями 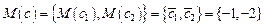 и ковариационной матрицей
и ковариационной матрицей 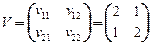 .
.
ЗСтП с целевой функцией на максимум в Р-постановке и ограничениями в Р-постановке. Решение - детерминированный вектор.
В6
А - детерминированная матрица 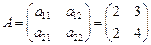 ,
,  - случайный вектор с заданными плотностями вероятностей компонент
- случайный вектор с заданными плотностями вероятностей компонент  ,
, 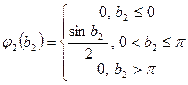 , с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями
, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями  и ковариационной матрицей
и ковариационной матрицей  . ЗСтП с целевой функцией на минимум в Р-постановке и ограничениями в Р-постановке. Решение - детерминированный вектор.
. ЗСтП с целевой функцией на минимум в Р-постановке и ограничениями в Р-постановке. Решение - детерминированный вектор.
В7
А - детерминированная матрица 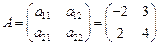 ,
,  - случайный вектор с заданными плотностями вероятностей компонент
- случайный вектор с заданными плотностями вероятностей компонент 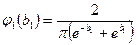 ,
, 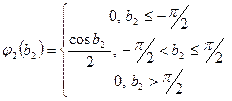 , с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями
, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями  и ковариационной матрицей
и ковариационной матрицей 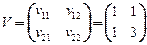 . ЗСтП с целевой функцией на минимум в P-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
. ЗСтП с целевой функцией на минимум в P-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
В8 А - детерминированная матрица  ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями  и дисперсиями. ЗСтП с целевой функцией на максимум в P-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
и дисперсиями. ЗСтП с целевой функцией на максимум в P-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
В9 А - детерминированная матрица  ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями  и дисперсиями
и дисперсиями 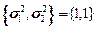 . ЗСтП с целевой функцией на максимум в М-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
. ЗСтП с целевой функцией на максимум в М-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
В10
А - детерминированная матрица 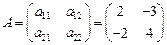 ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями  и дисперсиями
и дисперсиями 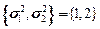 . ЗСтП с целевой функцией на максимум в P-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
. ЗСтП с целевой функцией на максимум в P-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
В11
А - детерминированная матрица 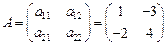 ,
,  - случайный вектор с заданными плотностями вероятностей компонент, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями
- случайный вектор с заданными плотностями вероятностей компонент, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями 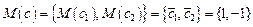 и ковариационной матрицей
и ковариационной матрицей 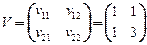 . ЗСтП с целевой функцией на минимум в Р-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
. ЗСтП с целевой функцией на минимум в Р-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
В12
А - детерминированная матрица  ,
,  - случайный вектор с заданными плотностями вероятностей компонент, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями
- случайный вектор с заданными плотностями вероятностей компонент, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями 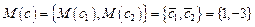 и ковариационной матрицей
и ковариационной матрицей  . ЗСтП с целевой функцией на минимум в K-постановке и ограничениями в P-постановке. Решение - детерминированный вектор.
. ЗСтП с целевой функцией на минимум в K-постановке и ограничениями в P-постановке. Решение - детерминированный вектор.
В13
Строки матрицы А и компоненты вектора  коррелированны, их компоненты - нормально распределенные случайные величины с заданными математическими ожиданиями
коррелированны, их компоненты - нормально распределенные случайные величины с заданными математическими ожиданиями  ,
, 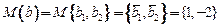 и ковариационными матрицами
и ковариационными матрицами 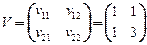 , с - детерминированный вектор
, с - детерминированный вектор 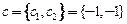 .
.
ЗСтП с ограничениями в Р-постановке. Решение - детерминированный вектор.
В14
А - детерминированная матрица  ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями  ,
, 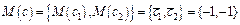 и дисперсиями
и дисперсиями 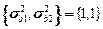
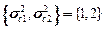 . ЗСтП с целевой функцией на максимум в P-постановке и ограничениями в M-постановке. Решения в виде линейных решающих правил.
. ЗСтП с целевой функцией на максимум в P-постановке и ограничениями в M-постановке. Решения в виде линейных решающих правил.
В15
А - детерминированная матрица 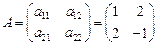 ,
,  - случайный вектор с заданными плотностями вероятностей компонент
- случайный вектор с заданными плотностями вероятностей компонент 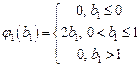 ,
, 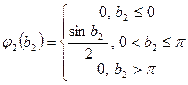 , с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями
, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями  и ковариационной матрицей
и ковариационной матрицей 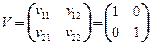 . ЗСтП с целевой функцией на минимум в P-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
. ЗСтП с целевой функцией на минимум в P-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
В16
А - детерминированная матрица 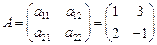 ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями 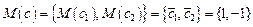 и дисперсиями
и дисперсиями 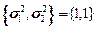 . ЗСтП с целевой функцией на максимум в V-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
. ЗСтП с целевой функцией на максимум в V-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
В17 А - детерминированная матрица  ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями  и дисперсиями
и дисперсиями 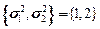 . ЗСтП с целевой функцией на максимум в М-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
. ЗСтП с целевой функцией на максимум в М-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
В18
А - детерминированная матрица 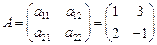 ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями 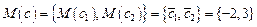 и дисперсиями
и дисперсиями  .
.
ЗСтП с целевой функцией на максимум в P-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
Форма отчета
1. Исходная постановка задачи
2. Параметры задачи
3. Детерминированный эквивалент ЗСтП
4. Графическое изображение множества планов детерминированного эквивалента ЗСтП и ее целевой функции
5. Решение детерминированного эквивалента в пакете
6. Интерпретация полученного решения для исходной ЗСтП
7. Детерминированный эквивалент для исходной задачи с целевой функцией и ограничениями в М-постановках.
8. Графическое изображение множества планов детерминированного эквивалента ЗСтП из п.7. и ее целевой функции (при различных значениях  -уровня)
-уровня)
9. Результаты исследования зависимости решения от  -уровня (от 0.5 до 0.9 с шагом 0.05) (в табличном и графическом виде)
-уровня (от 0.5 до 0.9 с шагом 0.05) (в табличном и графическом виде)
| № | 
| Оптимальный план | Оптимальное значение ЦФ |
| 0.5 | |||
| 0.55 |
График зависимости оптимального значения ЦФ от 
· Математическое ожидание и дисперсия целевой функции на найденном оптимальном решении (при  =0.5;
=0.5;  =0.9)
=0.9)
10. Выводы
Контрольные вопросы
Тема: «Модели и методы стохастического программирования»
1. Что может быть источником неопределенности информации в задачах планирования и управления? Приведите примеры.
2. Какие ситуации принятия решений называются ситуациями, связанными с риском?
3. Какие ситуации принятия решений называются неопределёнными?
4. Назовите и охарактеризуйте предмет стохастического программирования.
5. Какие ситуации принятия решения могут моделироваться стохастическими задачами?
6. Назовите и охарактеризуйте классы решений задач стохастического программирования.
7. Что такое информационная структура задачи? Какие бывают информационные структуры задач стохастического программирования?
8. Дайте содержательную постановку стохастической транспортной задачи (СТЗ).
9. Постройте мат. Модель СТЗ с непрерывно распределенным спросом, поясните все её компоненты.
10. Докажите выпуклость целевой функции СТЗ с непрерывно распределенным спросом.
11. Постройте детерминированный эквивалент СТЗ с дискретно распределенным спросом и поясните все его компоненты.
12. К какому классу задач детерминированной оптимизации относятся модель из вопроса 11?
13. Какие задачи относятся к одноэтапным задачам стохастического программирования?
14. Приведите М-постановку целевой функции ЗСтП. Поясните её суть.
15. Приведите P-постановку целевой функции ЗСтП. Поясните её cодержание.
16. Приведите К-постановку целевой функции ЗСтП. Поясните её суть.
17. Приведите V-постановку целевой функции ЗСтП. Поясните её суть.
18. Приведите М-постановку (статистические условия) ограничений ЗСтП. Поясните их суть.
19. Приведите P постановку (вероятностные ограничения) ограничений ЗСтП. Поясните их суть.
20. Как выполняются ограничения стохастической задачи на решении детерминированного аналога?
21. По каким причинам решение детерминированного аналога ЗСтП может давать неадекватное решение?
22. Что такое жесткая постановка ЗСтП и когда требуется такие постановки?
23. Для ЗСтП
 построить детерминированный эквивалент в случаях
построить детерминированный эквивалент в случаях
а) 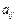 - детерминированные величины,
- детерминированные величины, 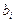 -случайные непрерывно распределенные величины с плотностью распределения
-случайные непрерывно распределенные величины с плотностью распределения 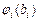
в) 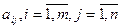 и
и 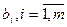 независимые между собой нормально распределенные случайные величины
независимые между собой нормально распределенные случайные величины
с) в дополнение к условиям в) случайные элементы условий (строки) коррелированны между собой.
22. Для ЗСтП

где  - нормально распределенные случайные величины, построить детерминированный эквивалент.
- нормально распределенные случайные величины, построить детерминированный эквивалент.
23. К какому классу задач оптимизации относятся построенные в пунктах 21.,22., детерминированные эквиваленты?
Пример 1.
1. Исходная постановка задачи.
ЗСтП с целевой функцией на минимум в KD-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
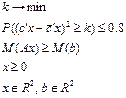
2. Параметры
А - детерминированная матрица:  ,
,  - случайный вектор с заданными плотностями вероятностей компонент,
- случайный вектор с заданными плотностями вероятностей компонент, 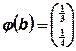 , с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями
, с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями 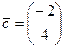 и ковариационной матрицей
и ковариационной матрицей 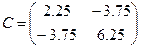 .
.
2. Детерминированный эквивалент ЗСтП.
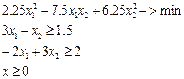 где
где 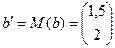 .
.
3. Графическое изображение множества планов детерминированного эквивалента ЗСтП.
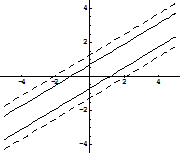
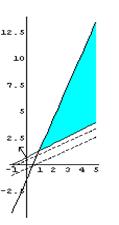
рис.1 рис.2
Т.к. на рис.2 линии уровня, соответствующие большему значению целевой функции (обозначены пунктиром) лежат выше линий уровня, соответствующих меньшему значению, то на рис.1 показан градиент.
4. Решение детерминированного эквивалента в пакете
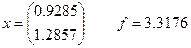
5. Интерпретация полученного решения для исходной ЗСтП
При  вероятность того, что дисперсия целевой функции больше наименьшего
вероятность того, что дисперсия целевой функции больше наименьшего  , меньше
, меньше  и в среднем ограничения выполняются.
и в среднем ограничения выполняются.
6. Детерминированный эквивалент для исходной задачи с целевой функцией и ограничениями в М-постановках.
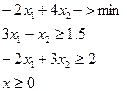
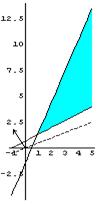
Пример 2.
1. Исходная постановка задачи.

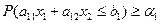
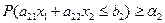
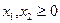
2. Параметры
А - детерминированная матрица 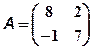 ,
,  ,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями и дисперсиями.
,с - независимые случайные векторы, компоненты которых - нормально распределенные случайные величины с заданными математическими ожиданиями и дисперсиями. 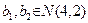 ,
,  - нормально распределенные случайные величины. ЗСтП с целевой функцией в М-постановке и Р-ограничениями. Решения в виде линейных решающих правил.
- нормально распределенные случайные величины. ЗСтП с целевой функцией в М-постановке и Р-ограничениями. Решения в виде линейных решающих правил. 
2. Детерминированный эквивалент ЗСтП.
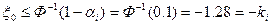
В итоге исходная стохастическая задача сводится к выпуклой детерминированной задаче:
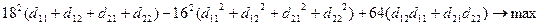

3. Графическое изображение множества планов детерминированного эквивалента ЗСтП.
4. Решение детерминированного эквивалента в пакете
 Значение целевой функции 4,35510177
Значение целевой функции 4,35510177
5. Интерпретация полученного решения для исходной ЗСтП
6. Детерминированный эквивалент для исходной задачи с целевой функцией и ограничениями в М-постановках.
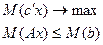


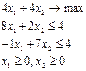
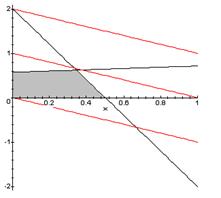
Решение:
| x= | 0,34482759 |
| 0,62068966 |
Значение целевой функции 3,86206897
Пример 3.
1. Исходная постановка задачи.
ЗСтП с целевой функцией на минимум в KD-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.

2. Параметры
А - детерминированная матрица: 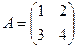 ,
,  - случайный вектор с заданными плотностями вероятностей компонент,
- случайный вектор с заданными плотностями вероятностей компонент,  с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями
с - случайный вектор, компоненты которого - коррелированные между собой нормально распределенные случайные величины с заданными математическими ожиданиями  и ковариационной матрицей.
и ковариационной матрицей. 
2. Детерминированный эквивалент ЗСтП.
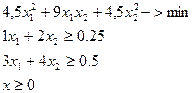 где
где 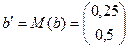 .
.
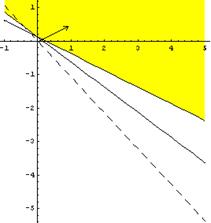
3. Графическое изображение множества планов детерминированного эквивалента ЗСтП.
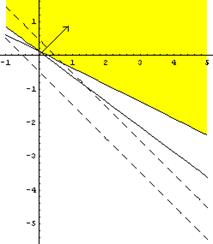 Рис1.
Рис1.
На рисунке линии уровня, которые соответствуют большему значению ц.ф. обозначены пунктиром. Линии уровня, которые соответствуют меньшему значению ц.ф. обозначены сплошной линией. Значит на Рис.1 изображен градиент.
Целевая функция:

4. Решение детерминированного эквивалента в пакете
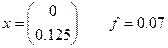
5. Интерпретация полученного решения для исходной ЗСтП
При  вероятность того, что диперсия целевой функции больше наименьшего
вероятность того, что диперсия целевой функции больше наименьшего 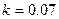 , меньше
, меньше 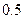 и в среднем ограничения выполняются.
и в среднем ограничения выполняются.
6. Детерминированный эквивалент для исходной задачи с целевой функцией и ограничениями в М-постановках.
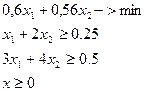
Пример 4.
| Задача стохастического программирования: | |||||||||

| |||||||||
| А - детерминированная матрица | |||||||||
| А= | |||||||||

| |||||||||
| b - случайный вектор с нормальной плотностью распределения | |||||||||

| |||||||||
| c - случайный вектор | |||||||||
| Матрица ковариации: | 
| ||||||||
| Решение - детерминированный вектор | |||||||||
| ОГРАНИЧЕНИЯ: | |||||||||
| |||||||||
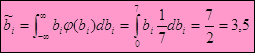
| |||||||||
| |||||||||
 Таким образом, Таким образом,
| |||||||||
| |||||||||
| ЦЕЛЕВАЯ ФУНКЦИЯ: | |||||||||
| |||||||||
| Детерминированный эквивалент: | |||||||||
| |||||||||
| 3,5 | |||||||||
| bi= | 3,5 | ||||||||
| ПОИСК РЕШЕНИЯ: | |||||||||
| F= | -2,176248 | ||||||||
| X= | 0,777778 | 3,5 | |||||||
| -0,388889 | 3,5 |