1. Скопируйте из прилагаемого файла «Выборка для студентов.xls» данные с листа под номером Вашего варианта в свой рабочий excel-файл. Первые три столбца в Вашем задании являются значениями технологических переменных процесса получения алюминия, последний столбец содержит значения показателя качества процесса или технологических нарушений.
2. По каждому столбцу данных рассчитайте среднее значение технологической переменной, сумму, минимальное и максимальное значение с помощью функций СУММ, СРЗНАЧ, МИН, МАКС Microsoft Excel.
3. По каждому столбцу рассчитайте дисперсию D и стандартное отклонение s технологической переменной двумя способами:
- с помощью формул 
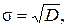
где xi – значение технологической переменной процесса;
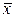– среднее значение технологической переменной;
n – количество измерений, которые можно рассчитать с помощью функции СЧЁТ;
- с помощью функций ДИСП, СТАНДОТКЛОН Microsoft Excel.
4. Постройте гистограмму распределения одной технологической переменной двумя способами. Методы построения приведены в приложении 1.
5. Найти парные коэффициенты корреляции между переменными с помощью функции КОРРЕЛ() Microsoft Excel. Построить корреляционную матрицу с помощью Анализа данных ® Корреляция (рисунок 1).
Столбец 1-3 – столбцы со значениями технологических переменных;
Столбец 4 – столбец со значениями показателя качества процесса
Рисунок 1 – Корреляционная матрица
6. Построить двумя способами парную линейную регрессию между переменными, имеющими наибольший по модулю коэффициент парной корреляции:
- по уравнению тренда на корреляционном поле соответствующих переменных. Например, на приведенном ниже графике Y – уровень металла, X – сила тока;
|
|
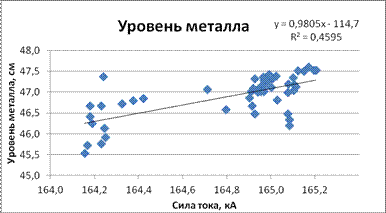
Рисунок 2 – Уравнение тренда на корреляционном поле
- с помощью пакета Анализ данных.
Опишем кратко последовательность действий:
1) Проверьте доступ к пакету анализа. В настройке панели быстрого доступа последовательно выберите Другие команды… ® Надстройки ® Пакет анализа и нажмите Перейти… Установите флажок Пакет анализа.
2) В главном меню выберите Данные ® Анализ данных ® Регрессия. Щелкните по кнопке ОК.
3) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон столбцов, содержащие значения факторов независимых признаков.
Результаты регрессионного анализа представлены в таблице 1.
Таблица 1.
Сделать выводы о качестве регрессионной модели.
7. Выбрать две переменные, имеющие наименьший коэффициент парной корреляции. Построить корреляционное поле (точечный график по этим двум переменным). Подобрать тренд – нелинейную функцию, наиболее качественно описывающую связь этих переменных.
8. Построить уравнение множественной линейной регрессии, которое описывает зависимость показателя качества процесса (выделить четвертый столбец) от трех переменных процесса (выделить три первых столбца) с помощью пакета анализ данных (таблица 2).
Таблица 2.
Уравнение получилось Y= 0,69∙X1 – 0,73∙X2 + 1,68∙X3 – 58,8.
Приложение 1