Формулировка задачи
По термодинамическим данным (таблица 1) для реакции (реакция взята из приложения А1)
 (1)
(1)
в интервале температур 300-750 К рассчитать изменения функций  ,
,  ,
,  ,
,  и
и  . Построить графики этих функций с температурным шагом 50 градусов. Проанализировать изменение этих функций при росте температуры. Сделать заключение о направлении реакции в расчетном интервале температур.
. Построить графики этих функций с температурным шагом 50 градусов. Проанализировать изменение этих функций при росте температуры. Сделать заключение о направлении реакции в расчетном интервале температур.
Составление таблицы термодинамических данных
Из приложения А2 сделать выборку термодинамических данных веществ реакции и поместить их в таблицу 1.
Табличные данные показывают, что в интервале температур 300-750 К происходит плавление твердого тетрахлорида тантала.
При температуре 570 К тетрахлорид тантала плавится. Следовательно, расчету подлежат две химические реакции:
 в интервале 300-570 К; (2)
в интервале 300-570 К; (2)
 в интервале 570-750 К. (3)
в интервале 570-750 К. (3)
3. Расчет изменения теплоемкости 
Изменения теплоемкости  реакций
реакций
Таблица 1-Термодинамические данные веществ реакции (III)
| Вещество | Фаза | 
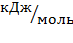
| 
 *K *K
|  К
К
| 
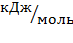
| Коэффициенты уравнения

 *K *K
| |||
| a | b | c | d | ||||||

| тв | -481,5 | 148,6 | 50,2 | 88,76 | 46,89 | - | - | |

| г | 130,6 | - | - | 27,72 | 3,39 | - | - | |

| тв | -586,2 | 196,8 | 21,8 | 110,1 | 38,5 | - | - | |

| ж | - | - | 83,7 | - | - | - | ||

| г | -95,46 | 186,8 | - | - | 28,05 | 3,52 | - | - |

| 
| |||

| 
| |||
| + | ||||

| 
| |||
| - | ||||

| 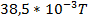
| |||
| - | ||||

| 
| |||

| 
| 
| (4) |

| 
| |||

| 
| |||
| + | ||||

| 
| |||
| - | ||||

| ||||
| - | ||||

| 
| |||

| 
| 
| (5) |
Сравнение уравнений (4) и (5) показывает, что фазовое превращение одного из веществ, приводит к изменению термодинамической характеристики реакции.
Расчет представим таблицей 2 и графиком (рисунок 1).
Таблица 2 - Расчетные значения  и
и  реакции(III)
реакции(III)

| 
| 
| 
|
| -7,15 | 3,065 | -4,086 | |
| -7,15 | 3,575 | -3,575 | |
| -7,15 | 4,086 | -3,064 | |
| -7,15 | 4,597 | -2,553 | |
| -7,15 | 5,108 | -2,043 | |
| -7,15 | 5,618 | -1,532 | |
| -7,15 | 5,823 | -1,327 |
Продолжение таблицы 2
| T, K | 
| 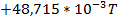
| 
|
| -48,05 | 27,768 | -20,282 | |
| -48,05 | 29,229 | -18,821 | |
| -48,05 | 31,665 | -16,385 | |
| -48,05 | 34,101 | -13,950 | |
| -48,05 | 36,536 | -11,514 |

Рисунок1 - Зависимость изменения теплоемкости реакции(III) от температуры
4. Расчет изменения энтальпии 
Изменение энтальпии реакции (1). В расчете учитываем, что в температурном интервале 300 – 750 К протекают две реакции (2) и (3). Это позволяет общее уравнение (4) представить двумя частями:
 (6)
(6)
для интервала 300 – 570 К. Уравнение (6) описывает широкий интервал температур, начиная со стандартной температуры.
 (7)
(7)
для интервала 570 – 750 К. В равенстве (7) эффект фазового превращения тетрахлорида тантала вычитается, так как это вещество является исходным. Видно, что необходимо определить  :
:




Представляем расчет таблицей 3 и графиком (рисунок 2)
Таблица 3 – Расчетные значения  реакции(1)
реакции(1)
| T, K | 
| 
| 
| 
| 
|
| 130153,17 | 3864,000 | 1526,400 | -1090,000 | 134453,570 | |
| 130153,17 | 4186,000 | 1791,400 | -1006,154 | 135124,416 | |
| 130153,17 | 4508,000 | 2077,600 | -934,286 | 135804,484 | |
| 130153,17 | 4688,320 | 2247,132 | -898,352 | 136190,271 |
Продолжение таблицы 3
| T, K | 
| 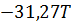
| 
| 
| 
|
| 118431,61 | -11382,280 | 1681,109 | -3140,110 | 105590,329 | |
| 118431,61 | -11726,250 | 1784,250 | -3048,000 | 105441,610 | |
| 118431,61 | -12508,000 | 2030,080 | -2857,500 | 105096,190 | |
| 118431,61 | -13289,750 | 2291,770 | -2689,412 | 104744,218 | |
| 118431,61 | -14071,500 | 2569,320 | -2540,000 | 104389,430 |

Рисунок 2 – Зависимость изменения энтальпии реакции (1) от температуры
Т.к.  до температуры фазового перехода, то
до температуры фазового перехода, то  будет возрастать на этом промежутке. после фазового перехода
будет возрастать на этом промежутке. после фазового перехода  и
и  будет убывать.
будет убывать.
5. Расчет изменения энтропии 
Изменение энтальпии реакции (1). И опять учитываем, что в температурном интервале 300 – 450 К протекают две реакции (2) и(3), поэтому изменение энтропии будем считать по двум уравнениям:
 (8)
(8)
для интервала 300 – 364 К.
 (9)
(9)
для интервала 364 – 450 К. Определяем  :
:




Расчет по уравнениям (8) и (9) представим таблицей 4 и графиком (рисунок 3).
Таблица 4 – Расчетные значения  реакции (III)
реакции (III)
| T, K | 
| 
| 
| 
| 
|
| 99,399 | 73,465 | 10,175 | -1,817 | 181,222 | |
| 99,399 | 74,496 | 11,022 | -1,548 | 183,369 | |
| 99,399 | 75,450 | 11,870 | -1,335 | 185,385 | |
| 99,399 | 75,955 | 12,345 | -1,234 | 186,465 |
Продолжение таблицы 3
| T, K | 
| 
| 
| 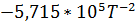
| 
|
| 281,872 | -184,404 | 9,237 | -4,313 | 102,391 | |
| 281,872 | -185,335 | 9,516 | -4,064 | 101,989 | |
| 281,872 | -187,353 | 10,150 | -3,572 | 101,097 | |
| 281,872 | -189,249 | 10,784 | -3,164 | 100,244 | |
| 281,872 | -191,036 | 11,419 | -2,822 | 99,432 |

Рисунок 3 - Зависимость изменения энтропии реакции (1) от температуры
Сравним графики рисунков 2 и 3. Видим, что поведение обеих функций при изменении температуры подобно. Так и должно быть, так как обе функции описываются изменением теплоемкости реакции.
6. Расчет изменения энергии Гиббса 
Изменение энергии Гиббса реакции (1). Расчет представим таблицей 5 и графиком (рисунок 4). Обратим внимание на то, что  не претерпевает разрыва при температуре фазового превращения в отличие от функций
не претерпевает разрыва при температуре фазового превращения в отличие от функций  и
и  . Это верно и следует из уравнения (10), записанного для температуры фазового перехода:
. Это верно и следует из уравнения (10), записанного для температуры фазового перехода:
 (10)
(10)
Таблица5-Расчетные значения  реакции(III)
реакции(III)
| T, K | 
| 
| 
| 
|
| 181,222 | 54366,465 | |||
| 183,369 | 59594,962 | |||
| 185,385 | 64884,657 | |||
| 186,465 | 67873,406 | |||
| 102,391 | 37270,383 | |||
| 101,989 | 38245,743 | |||
| 101,097 | 40438,811 | |||
| 100,244 | 42603,501 | |||
| 99,432 | 44744,560 |
Для анализа полученной зависимости нужно воспользоваться следующим дифференциальным уравнением:
 (11)
(11)
В нашем расчете изменение энтропии реакции (1) во всем расчетном интервале температур меньше нуля. Следовательно, производная уравнения (11) положительна, что делает  возрастающей функцией при росте температуры. Рисунок 4 это иллюстрирует.
возрастающей функцией при росте температуры. Рисунок 4 это иллюстрирует.

Рисунок 4 - Зависимость изменения энергии Гиббса реакции (III) от температуры