Система отсчета, относительно которой выполняется закон Ньютона, называется инерциальной.
Второй закон Ньютона: изменение движения пропорционально приложенной силе и происходит в том направлении, в каком действует сила.
Сила – это физическая величина, характеризующая взаимодействие тел, в результате оторого тела приобретают ускорения или деформируются [F]=[Н]=[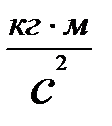 
].
Но разные тела под влиянием одинаковых сил приобретают разные ускорения, следовательно, ускорение зависит не только от силы, но и от собственных свойств тел. Это свойство называется массой.
Масса – это мера инертности тела [m] = [кг].
Инертность – это способность тела приобретать ускорение.
1Н – сила, сообщающая телу массой 1кг ускорение 1м/с2 в направлении действия силы.
Запишем второй закон Ньютона
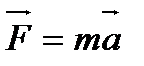, (1)
но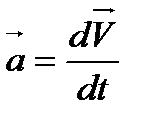 
, следовательно,
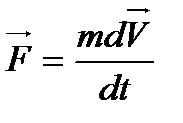. (2)
Подведем m под знак дифференциала
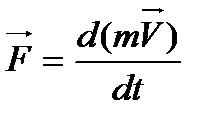, но
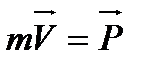(3)
импульс (количество движения).
[Р]=[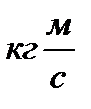 
] направление импульса совпадает с направлением силы.
Перепишем второй закон Ньютона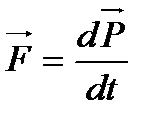 
;
. (9)
второй закон Ньютона через импульс
Динамические уравнения движения – это второй закон Ньютона, записанный для данного тела. Эти уравнения можно записать в векторном виде и в проекциях на оси координат. Составление и решение таких уравнений – главная задача динамики.
Движение твердого тела можно охарактеризовать двумя видами: поступательным и вращательным (из них состоит любое сложное движение).
При поступательном движении тела все его точки двигаются с одинаковыми скоростями и ускорениями. Если мысленно разбить тело наэлементами с массами Dmi, то по второму закону Ньютона получим
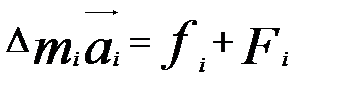, (4)
где fi – внутренняя сила (сила взаимодействия элементов тела);
Fi – внешняя сила, действующая на каждый элемент.
По третьему закону Ньютона сумма вех внутренних сил равна 0, поэтому, суммируя выражения, получим
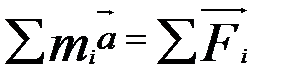(5)
или
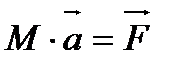, (6)
где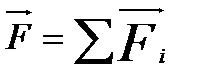 
– векторная сумма всех внешних сил;
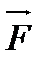– главный вектор внешних сил.
Следовательно, рассмотрение поступательного движения твердого тела можно заменить рассмотрением движения одной материальной точки с массой, равной массе тела, и находящейся под действием силы, равной главному вектору внешних сил.
При сложном движении тела все его точки имеют разные скорости и ускорения. Разобьем тело на столь малые элементы, что их скорости и ускорения остаются постоянными
.
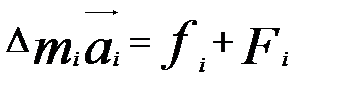Суммируем это равенство fi = 0
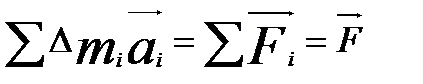(7)
главный вектор внешних сил
Однако ускорения всех элементов тела разные, поэтому введем ускорение ас, определяемое равенством
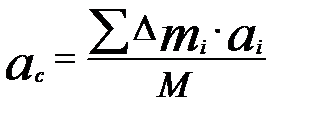, (8)
где М – масса всего тела.
Умножим левую и правую часть равенства на М, используя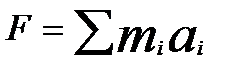 
, получим
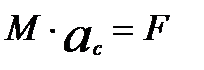, (9)
где ас – ускорение некоторой точки С, координаты которой
; 
; 
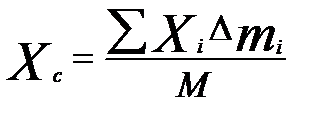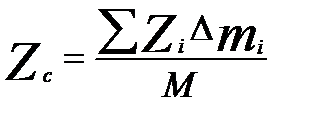, (10)
где С – центр масс тела или центр инерции (совпадает с центром приложения равнодействующей сил тяже).
15. Сложение двух гармонических колебаний одинаковой циклической частоты, происходящих вдоль одной прямой.
Пусть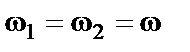 
; 
; 
.
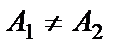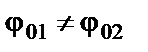Складываемые колебания описываются уравнениями:
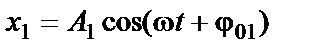; (1)
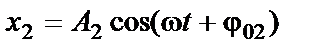. (2)
Так как колебания происходят вдоль одной прямой (вдоль оси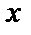 
), то результирующее смещение в любой момент времени равно алгебраической сумме смещений 
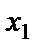и 
:
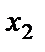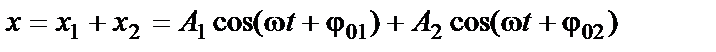(3)
Выполним это сложение геометрически, с помощью векторов амплитуды 
и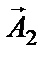 
. На рисунке1 изображены положения векторов амплитуды в начальный момент времени. Вектор результирующей амплитуды 
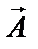равен геометрической сумме векторов 
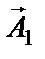и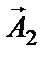 
.
Проекции конца вектора 
определяет результирующее смещение в начальный момент времени. Так как оба вектора,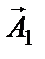 
и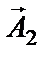 
, вращаются в процессе колебаний с одной и той же угловой скоростью 
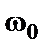, с такой же скоростью будет вращаться и вектор результирующей амплитуды. Следовательно, результирующее колебание представляет собой гармоническое колебание той же частоты и происходит вдоль той же прямой. Из рисунка 1 видно, что
,
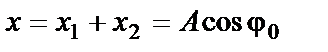для произвольного момента времени:
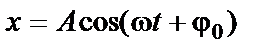, (4)
где 
и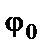 
- амплитуда и начальная фаза результирующего колебания. Из 
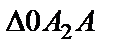по теореме косинусов получаем:
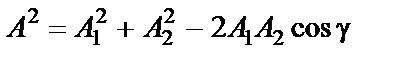
Рисунок 1
или
(5)
так как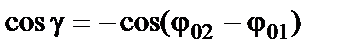 
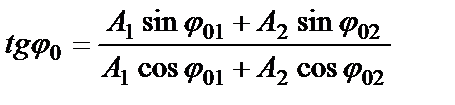(6)
Амплитуда результирующего колебания зависит от разности фаз (
) слагаемых колебаний. Если (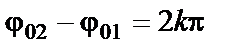
), где 
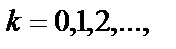то 
и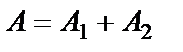 
, т.е. если разность фаз равна четному числу 
, колебания усиливают друг друга. Если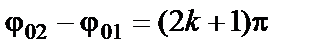 
, то 
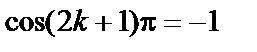и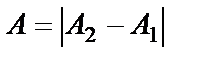 
, т.е.
если разность фаз равна нечетному числу 
, колебания максимально ослабляют друг друга. В зависимости от разности фаз амплитуда колебания может принимать любые значения, лежащие в интервале:
.
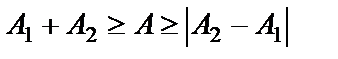