Теорема о трех перпендикулярах

Теорема.

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.

Доказательство.

Пусть AB – перпендикуляр к плоскости α, AC – наклонная и с – прямая в плоскости α, проходящая через основание С наклонной. Проведем прямую CA` параллельную прямой AB. Она перпендикулярна плоскости α. Проведем через прямые AB и A`C плоскость β. Прямая с перпендикулярна прямой CA`. Если она перпендикулярна прямой CB, то она перпендикулярна плоскости α, а значит, и прямой AC.

Обратная теорема о трех перпендикулярах Теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. Доказательство. Аналогично теореме о трех перпендикулярах если прямая с перпендикулярна наклонной CA, то она, будучи перпендикулярна и прямой CA`, перпендикулярна плоскости β, а значит, и проекции наклонной BC. Теорема доказана.

Перпендикулярные плоскости Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым. Плоскость α перпендикулярна плоскости β. Они пересекаются по прямой с. Плоскость γ перпендикулярна с и пересекает плоскости α и β по прямым a и b соответственно.

Признак перпендикулярности плоскостей

Теорема

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство

Пусть α - плоскость, b – перпендикулярная ей прямая, β - плоскость, проходящая через прямую b, и с – прямая, по которой пересекаются плоскости α и β. Следует доказать, что α и β перпендикулярны.
Проведем в плоскости α через точку пересечения прямой b с плоскостью α прямую a, перпендикулярную прямой с. Проведем через прямые a и b плоскость γ. Она перпендикулярна прямой с, так как прямая с перпендикулярна прямым a и b. Так как прямые a и b перпендикулярны, то плоскости α и β перпендикулярны. Теорема доказана.

Расстояние между скрещивающимися прямыми Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них. Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходящими через эти прямые.

Расстояние между скрещивающимися прямыми. Свойства Теорема Две скрещивающиеся прямые имеют общий перпендикуляр, и при том только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые. 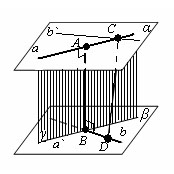Доказательство Пусть a и b – данные скрещивающиеся прямые. Проведем через них параллельные плоскости α и β. Прямые, пересекающие прямую a и перпендикулярные плоскости α, лежат в одной плоскости (γ). Эта плоскость пересекает плоскость β по прямой a`, параллельной a. Пусть B – точка пересечения прямых a` и b. Тогда прямая AB, перпендикулярная плоскости α, перпендикулярна и плоскости β, так как β параллельна α. Отрезок AB – общий перпендикуляр плоскостей α и β, а значит, и прямых a и b. Докажем, что этот общий перпендикуляр единственный. Допустим, что у прямых a и b есть другой общий перпендикуляр CD. Проведем через точку С прямую b`, параллельную b. Прямая CD перпендикулярна прямой b, а значит, и b`. Так как она перпендикулярна прямой a, то она перпендикулярна плоскости α, а значит, параллельна прямой AB. Выходит, что через прямые AB и CD, как через параллельные, можно провести плоскость. В этой плоскости будут лежать наши скрещивающиеся прямые AC и BD, а это невозможно, что и требовалось доказать.