Крепление полосы к косынке 20

ПРИМЕРЫРАСЧЁТА

РЕЗЬБОВЫХ И СВАРНЫХ СОЕДИНЕНИЙ

 

Для студентов специальностей 150700 - Локомотивы

150800 - Вагоны

170900 - Подъёмно-транспортные,

строительные и дорожные

машины и оборудование

181400 - Электрический транспорт

железных дорог.

 

 

Составители: Толстоногов А.А.,

Янковский В.В,

Глобенко Е.В.

.

 

Самара 2002 г.

 

УДК 621.81(075.8)

Методические указания к выполнению расчётно-графических работ по дисциплине "Детали машин" для студентов специальностей 150700, 150800, 170900 / Составители Толстоногов А.А., Янковский В.В., Глобенко Е.В, Самара, СамИИТ, 2002.- 35 с.

 

Утверждено на заседании кафедры, протокол № 2 от 8.10.2002г.

Печатается по решению редакционно-издательского совета академии.

 

 

Составители: Толстоногов Андрей Арленович,

Янковский Виктор Владимирович.

Глобенко Евгений Викторович,

 

Рецензенты: Доцент кафедры ОКМ СГАУ Жильников Е.П.

Доцент кафедры механики СамИИТ Фёдоров В.В.

 

Редактор: Шимина И.А.

 

Подписано в печать 33.33.2002 Формат 60х84 1.16

Бумага писчая. Усл. печ. л 2,24

Тираж 100 экз. Заказ №

 

© Самарская Государственная Академия Путей Сообщения, 2002.

 

ОГЛАВЛЕНИЕ

 

1. Введение 4

2. Резьбовые соединения 4

2.1. Общие принципы расчёта резьбовых соединений 4

2.2. Примеры расчёта резьбовых соединений 5

2.2.1. Расчёт силы затяжки болта 5

2.2.2. Крепление клеммного рычага 7

2.2.3. Крепление пластины 9

2.2.4. Крепление подшипника вала ременной передачи 12

2.2.5. Болты фланцевой муфты 14

Крепление крышки газового резервуара 16

3. Сварные соединения 17

3.1. Общие принципы расчёта сварных соединений 17

3.2. Примеры расчёта сварных соединений 18

3.2.1. Крепление раскоса 18

Крепление полосы к косынке 20

3.2.3. Сварка стальных полос 22

3.2.4. Комбинированный шов 23

3.2.5. Консольное соединение 25

3.2.6. Крепление уголка 27

3.2.7. Крепление кронштейна корпуса подшипника 28

3.2.8. Крепление кронштейна 30

3.2.9. Консольное крепление трубы 32

Приложения 33

Литература 35

 

1. Введение

 

Соединения деталей – конструктивная реализация составления деталей для образования из них частей машины. Под соединениями в машиностроении понимают соединительные детали и прилегающие к ним части соединяемых деталей

Главнейшим классификационным признаком соединений является возможность разборки, поэтому все их виды можно отнести к двум группам: разъёмные и неразъёмные.

Разъёмные соединения допускают разборку без разрушения каких-либо элементов (резьбовые, клиновые, шлицевые, шпоночные, штифтовые и т.п.).

Неразъёмные соединения для разборки требуют полного или частичного разрушения элементов (сварные, паяные, клеевые, клёпаные и т.п.).

Ярчайшими представителями этих двух групп являются соответственно резьбовые и сварные соединения. Их широкое применение обусловлено высокой стандартизацией, технологичностью, надёжностью. Практически ни один механизм, агрегат или машина не обходятся без сварных, а уж тем более без резьбовых соединений.

Поэтому освоение навыков расчёта резьбовых и сварных соединений очень важно для будущих инженеров.

 

 

2. Резьбовые соединения

 

Резьбовыми называют разъёмные соединения, образуемые специальными деталями – винтами и гайками, имеющими специальные винтовые канавки, называемые резьбой. Применяются повсеместно. Конструкции и расчёту резьбовых соединений посвящена обширная литература.

 

2.1. Общие принципы расчёта резьбовых соединений

 

Чаще всего расчёт резьбовых соединений выполняется на стадии проектирования машины, когда конструктор задаёт число и расположение болтов, а затем определяет их диаметр (номер). Иногда возникает необходимость проверить прочность болтов уже спроектированной машины, например, при назначении других условий её работы.

В процессе работы детали резьбовых соединений испытывают либо растяжение, либо срез и смятие в зависимости от схемы приложения сил и от наличия зазоров между болтами и отверстиями соединяемых деталей.

В любом случае необходимо знать силы, действующие на каждый болт или винт, а затем в зависимости от вида расчёта либо определять требуемый диаметр болтов (проектировочный расчёт) либо оценить прочность назначенных болтов, сравнивая их напряжения с допускаемыми.

При этом нельзя забывать, что главный недостаток резьбовых соединений – концентрация напряжений во впадинах резьбы, что обязательно должно учитываться корректным назначением допускаемых напряжений.

 

2.2. Примеры расчёта резьбовых соединений

2.2.1. Расчёт силы затяжки болта

 

Определить силу F_зат ,которую необходимо приложить к стандартному ключу при завинчивании гайки (Рис. 2.2.1) до появления в стержне болта напряжений, равных пределу текучести σ_т = 200 МПа (сталь 10). Определить также напряжения смятия σ_см и среза τ в резьбе. Расчет выполнить для болтов М6, М12, М36 и сравнить полученные результаты. Длину ручки стандартного ключа в среднем принять l = 15d, коэффициент трения в резьбе и на торце гайки f = 0,15.

 

Используя таблицы стандартов, находим необходимые для расчетов размеры (Табл. 1 Прил.).

Сила затяжки, при которой эквивалентное напряжение в стержне болта равно σ_т для болта М6

Момент завинчивания

Здесь принято:

Приведённый коэффициент трения в резьбе

Угол трения

Сила, приложенная к гаечному ключу

Выигрыш в силе F_зат /F_к = 2900 / 39 ≈74 раза.

Напряжения в резьбе при F = F_зат (z=5 – число рабочих витков гайки)

Касательные напряжения среза (высота гайки 5мм; коэффициент полноты треугольной резьбы 0,87; коэффициент неравномерности нагрузки по виткам резьбы 0,6)

Результаты расчетов для других болтов получены аналогично и сведены в таблицу

 

Силовые параметры при затяжке болтов до напряжения σэк=200 Мпа (сталь10)	Болт
М6	М12	М24	М36
Сила затяжки Fзат, Н
Момент завинчивания Тзав, Нм	3,5	32,7
Сила на ключе Fк, Н
Выигрыш в силе Fзат/ Fк
Напряжения смятия в резьбе σсм, МПа
Напряжения среза в резьбе τ, МПа		77,8

 

Из результатов расчёта видно, что болты малого диаметра (до М8) можно легко разрушить при затяжке, так как человек может приложить к ключу силу F_к до 200 Н, а нагрузочную способность болтов большого диаметра (больше М24) трудно использовать полностью. Напряжения смятия σ_см не превышают напряжений среза τ, а допускаемые напряжения [σ_см] в два раза больше [τ]. При этом прочность крепежных резьб по σ_см более чем в два раза превышает прочность по τ. Крепежные резьбы можно не рассчитывать по σ_см.

 

2.2.2. Крепление клеммного рычага

 

Определить требуемые усилия затяжки болтов для двух вариантов крепления рычага к головке клеммы.

 

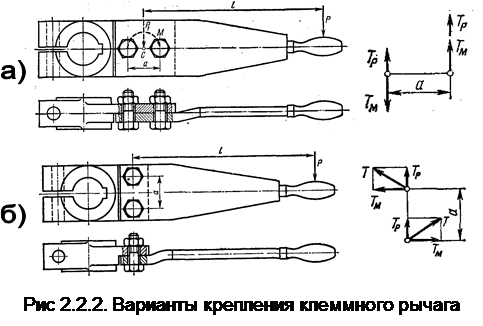Силу Р, действующую на рычаг, приводим по правилам статики к центру тяжести болтового соединения точке С (рис. 2.2.2.а).В результате в плоскости стыка получаем силу Р₁ = Р и момент М = Р×l. Сила и момент должны быть уравновешены силами трения, вызванными затяж­кой болтов. Условно примем, что точки приложения равнодействующих сил трения совпадают с центрами тяжести болтовых отверстий рычага. Действие силы Р₁ и момента рассматриваем раздельно. Сила P₁ уравновешивается силами Т_р, каждая из которых равна 0,5P₁=0,5P (рис. 2.2.2.а). Момент М уравновешивается моментом пар сил T_M:

Наибольшая сила трения

должна быть обеспечена затяжкой правого болта; с учетом увеличения затяжки на 20% по сравнению с минимально необходимой имеем

Расчет на прочность надо выполнить для более нагруженного правого болта; второй (левый) болт следует принять такого же диаметра, как и пер­вый (правый). Для схемы на рис 2.2.2.б силы трения, уравновешивают сдвигающую силу Р и момент М = Рl. По-прежнему

но в этом случае силы T_M направлены горизонтально. Суммарные силы трения

для обоих болтов одинаковы, а, следовательно, и величины затяжки этих болтов также одинаковы:

Для второго случая величина силы затяжки V меньше, чем для первого, а значит:

.

 

Крепление пластины

 

Рассчитать болты крепления пластины, нагруженного силой R (рис. 2.2.3). Расчет выполнить для двух вариантов установки болтов — без зазора и с зазором.

 

R = 20 000 H; l =1050 мм; a = 130 мм; b = 500 мм, d = 20 мм, кронштейн стальной (s_т = 240 МПа); болты из стали 20.

 

Общие указания

При расчете соединения силу R заменяем такой же силой, приложенной в центре тяжести стыка, и моментом T = R*l. Момент и сила стремятся повернуть и сдвинуть пластину. Нагрузка от силы R распределяется по болтам равномерно:

F_R = R/z.

Нагрузки от момента (реакции F_T1, F_T1,.., F_T1Z ) распределяются по болтам пропорционально их деформациям при повороте пластины. В свою очередь, деформации пропорциональны расстояниям бол­тов от центра тяжести стыка, который является центром поворота. Направление реакций болтов перпендикулярно радиусам r₁, r₂ ,..., r _Z.

По условию равновесия

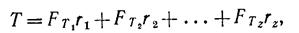
где

Для конструкции, показанной на рисунке 2.2.3:

Суммарная нагрузка каждого болта равна геометрической сумме соответствующих сил F_R и F_T (на рис. 2.2.3 показана нагрузка для первого болта F₁).

За расчетную принимают наибольшую из суммарных нагрузок. Сравнивая значения и направление реакций, можно отметить, что для соединения, изображенного на рис. 2.2.3, наиболее нагруженными болтами являются 1-й и 3-й (реакции F_R и F_T близки по направлению) или 2-й (F_R и F_T направлены одинаково, но F_T2 < F_T1 и F_T3).

В конструкции соединения болты могут быть поставлены без за­зора или с зазором.

Болты без зазора непосредственно воспринимают нагрузку. Прочность болтов и деталей рассчитывают по напряжениям среза и смятия

,

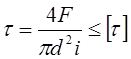где i - число плоскостей среза.

.

При установке болтов с зазором нагрузка воспринимается силами трения стыков, для чего болты соответственно затягиваются. Соединение будет прочным (детали не сдвигаются) если равнодействующая сил трения под каждым болтом не меньше, чем равнодействующая сил F_R и F_T. Необходимая затяжка болтов

F_зат = K * F_max / f,

Где K – коэффициент запаса, F_max – сила, приходящаяся на наиболее нагруженный болт, f - коэффициент трения.

Прочность болтов рассчитывают по формуле

.

 

Решение

Болты без зазора.

где F_T1/F_T2 = r₁/r₂; r₂= b/2 = 250 мм;

T

Далее,

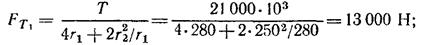
Для первого и третьего болтов суммарную нагрузку находим графически (см. рис. 2.2.3) и получаем F₁ = F₃ = 16000 Н. Для второго болта

Таким образом, наиболее нагруженными являются болты 1 и 3. Определяем диаметр болтов из условия прочности на срез:

где [t] = 0,4s_T = 0,4*240 =96 МПа.

Найденному значению d удовлетворяет чистый болт под развертку с диаметром нарезной части М16 и ненарезной 17 мм.

Проверяем прочность на смятие по формуле:

Болты с зазором.

Необходимую силу затяжки определяем по формуле

приняв F_max = F₁ = 16000 Н, f = 0,15; K = 1,5;

F_зат = 1,5 * 16000 / 0,15 = 160000 H.

Для контролируемой затяжки принимаем [s]=1,5. При этом

Из формулы s_эк = 1,3*4*F/pd² < [s_эк] определяем:

Этому значению d₁ удовлетворяет болт М48.

 

Заключение.

Постановка болтов с зазором в данной конструкции нецелесооб­разна, так как болт М48 слишком велик для такого кронштейна и, кроме того, трудно обеспечить силу затяжки болтов F_зат= 160000 Н.

Назначаем болты без зазора.

 

2.2.4. Крепление подшипника вала ременной передачи

 

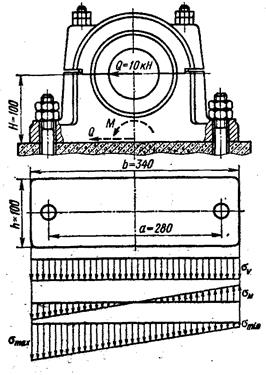
Подшипник вала ременной передачи укреплен на бетон­ном основании двумя фундаментными болтами (рис. 2.2.4). Опре­делить диаметр болтов, изготовленных из СтЗ. Коэффи­циент трения в стыке f = 0,35.

Рис 2.2.4. Крепление подшипника

 

 

Решение.

Приводим силу Q к центру тяжести стыка; в результате получаем сдви­гающую силу Q и момент M = Q H, стремящийся повернуть подшипник.

Затяжка болтов должна гарантировать нераскрытие стыка и отсутствие сдвига подшипника по основанию. От затяжки болтов на стыке возникают напряжения смятия s_V, которые можно считать распределенными по площади стыка равномерно (см. эпюру на рис. 2.2.4);

где V — сила затяжки каждого болта;

F_ст = bh — площадь стыка.

От действия момента на левой половине стыка напряжения смятия воз­растают, а на правой — уменьшаются. Принимаем, что напряжения на стыке от момента распределены по линейному закону ана­логично распределению напряжений изгиба при нейтральной оси, совпадающей с осью симметрии стыка. Тогда наибольшие напряжения от момента

По условию нераскрытия стыка

т. е. в данном случае

С учетом запаса по нераскрытию стыка

Приняв К_ст = 2 (обычно принимают K_ст = 1,3 ¸ 2), получим

Сила затяжки болта

Проверяем достаточность затяжки болтов по условию отсутствия сдвига подшипника; при этом считаем, что сила трения, вызванная затяжкой болтов, должна быть на 20% больше минимально необходимой, т. е.

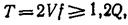
или

T = 2*17,63*0,35 = 12,35 кН; 1,2Q = 1,2*10=12 кН.

Неравенство выполняется.

Максимальные напряжения смятия (возникающие на левой кромке стыка) должны быть не выше [s]_см = 2,0 Н/мм² (допускаемое напряжение смятия для бетона);

это условие также удовлетворяется.

Наиболее нагружен правый болт, воспринимающий внешнюю растягиваю­щую нагрузку от действия момента:

Учитывая массивность основания, на котором установлен подшипник, принимаем коэффициент внешней нагрузки c= 0,15, тогда суммарная осевая нагрузка правого болта

По таблице 2 приложения предполагая, что затяжка болтов не контролируется, уста­навливаем, что такая нагрузка допустима для болта с резьбой М22.

 

2.2.5. Болты фланцевой муфты

 

Рассчитать болты фланцевой муфты (рис. 2.2.5) при условии, что передаваемая мощность N = 40 КВт, частота вращения муфты n = 100 об/мин, диаметр окружности центров болтов D₀ = 236 мм и число болтов z = 6. Расчет выполнить для двух случаев: а) болты установлены с зазором; б) болты установлены без зазора. Коэффициент трения между полу­муфтами f = 0,2. Нагрузка постоянная.

 

 

 

Решение.

Определяем крутящий момент, передаваемый муфтой,

Окружное усилие, приходящееся на один болт,

При расчете болтов с зазором определяем внутренний диаметр болта из условия прочности на растяжение, приняв материал болтов — Ст20 s_T = 260 Н/мм²

Допускаемое напряжение при [S] = 3:

По ГОСТ 9150—59 выбираем болт с ближайшим большим внутренним диа­метром d₁= 23,752 мм, что соответствует болту М27 с крупным шагом, номинальный диаметр которого равен 27 мм.

При расчете болтов без зазора определяем наружный диаметр болта из условия прочности на срез, приняв материал болта—сталь 20 (s_T = 260 Н/мм²), а допускаемое напряжение среза

Принимаем болт М10, так как болт с диаметром стержня d = 8 мм мал.

 

2.2.6. Крепление крышки газового резервуара

 

Определить диаметр резьбы болтов, крепящих крышку газового резерву­ара (см. рис. 2.2.6), если сила давления газа на крышку F_K = 55 кН, число болтов z= 8. Нагрузка постоянная. Материал болтов Ст35, класс прочности 5.6. Материал прокла­док — паронит. Затяжка болтов динамометрическим ключом.

 

Решение.

Для резьбового соединения с контролируемой затяжкой принимаем [S]_T = 2. По табл.3 Приложения находим s_T = 300 Н/мм².

Допускаемое напряжение растяжения

Нагрузка на один болт

Для обеспечения герметичности соединения устанавливают паронитовую проклад­ку, а болты затягивают с силой, обеспечивающей нераскрытие стыка. Принимаем: К_зат=1,75; c = 0,45.

Сила предварительной затяжки

Расчетная сила

Расчетный диаметр резьбы болта

Принимаем резьбу М12 с шагом p = 1,75 мм, для которой d_P = 10,36мм > 9,96мм. Болт М12 пригоден.

 

 

3. Сварные соединения

 

Сварными называют соединения, выполняемые за счёт местного нагрева и диффузии (перемешивания частиц) соединяемых деталей. При этом создаётся, практически монолитная деталь. Эти соединения весьма прочны, т.к. используют силы межмолекулярного сцепления. Не требуют соединяющих деталей. Имеют широчайшее применение в машиностроении, в том числе на железнодорожном транспорте.

 

 

3.1. Общие принципы расчёта сварных соединений

 

Обычно расчёт сварных соединений выполняется на стадии проектирования машины, когда известен общий вид конструкции, примерное расположение и длина швов, по справочным данным назначена марка электрода, определены допускаемые напряжения и толщина (катет) шва. В результате оценивается прочность назначенных сварных швов, т.е. расчёт, в сущности, является проверочным.

В любом случае для расчёта самых сложных сварных швов сначала необходимо привести силу и момент к шву и распределить их пропорционально несущей способности (длине) всех простых участков. Таким образом любой сложный шов сводится к комбинации простейших расчётных схем: лобовых, фланговых, косых, тавровых и угловых.

 

 

3.2. Примеры расчёта сварных соединений

3.2.1. Крепление раскоса

 

Сжатый раскос фермы имеет свободную длину 3 м, его концы считать закрепленными шарнирно. Продольная сила, возникающая при нагружении фермы в поперечном сечении раскоса, N = 250 кН.

 

 

Подобрать сечение раскоса из двух равнобоких угол­ков и определить длину фланговых швов, которыми он приварен к косынке. Материал раскоса — СтЗ. Сварка электродами Э42 вручную.

 

Решение.

Определяем требуемую площадь сечения раскоса с учетом понижения допускаемого напряжения:

для стали СтЗ [s]_C = [s]_р = 160 Н/мм².

Коэффициент j продольного изгиба зависит от гибкости стержня (раскоса), которая пока неизвестна. Поэтому в начале расчета надо задаться коэффи­циентом j ориентировочно. Принимаем j = 0,5, при этом

Требуемая площадь сечения одного уголка

Принимаем уголки 100х100х8 мм по ГОСТ 8509—72 (F₁ = 15,6 см²) и проверяем гибкость стержня:

где m = 1 — коэффициент приведения длины;

i_min — минимальный радиус инерции сечения.

Минимальный главный центральный момент инерции сечения раскоса будет относительно оси х

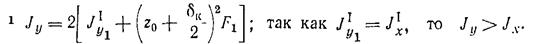
Учитывая, что радиус инерции относительно оси х сечения из двух уголков равен i_x одного уголка.

При l =98, j_таб = 0,618.

Так как j_таб оказалось больше принятого предварительно, производим перерасчет, принимая новое значение j равным среднему арифметическому между предварительно выбранным и полученным;

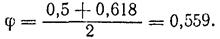
Требуемая площадь сечения уголка

 

Принимаем уголок 90х90х8 мм; F₁ =13,9 см²; i_x = 2,70 см.

Гибкость

Этой гибкости соответствует j_таб = 0,528. Так как это значение меньше предварительного принятого, то напряжения в стержне будут выше допу­скаемых:

Допускаемое напряжение

Превышение рабочих напряжении над допускаемыми составляет примерно 0,4%, поэтому надо принять уголки несколько большого сечения или с боль­шим радиусом инерции. Принимаем уголки 100х100х0,5, для которых F₁ = 12,8 см²; i_x =3,09 см, тогда

 

допускаемое напряжение

расчетное напряжение

что меньше допускаемого на 2,4%.

Суммарная длина фланговых швов для прикрепления уголка

Принимаем катет шва k = 8 мм. Допускаемое напряжение для сварного шва на срез