Лекция №3
Векторное произведение векторов.
Геометрический смысл векторного произведения. Площадь треугольника. Смешанное произведение векторов.
Геометрический смысл смешанного произведения. Объем тетраэдра
Определение 3.1. Векторным произведением двух неколлинеарных и ненулевых векторов 
и 
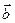, взятых в определенном порядке, называется такой вектор 
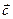, что:
1. 
;
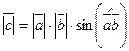2. 
;
3. 
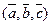- тройка положительно ориентирована и одинаково ориентирована с базисом, в котором она рассматривается.
Обозначается 
Свойства векторного произведения.
1) Векторное произведение векторов и 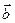равно нулевому вектору, если один из векторов нулевой или векторы и 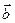коллинеарны: 
или 
2) При перемене порядка сомножителей векторное произведение не меняет своего модуля, но меняет направление на противоположное: 
3) Сочетательное свойство векторного произведения при умножении на скаляр выражается равенством: 
4) Распределительное свойство векторного произведения выражается равенством: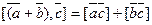 
5) Векторное произведение не изменится, если один из сомножителей, например, вектор 
заменить его проекцией вектором 
на прямую, лежащую в плоскости векторов и 
и перпендикулярную к : 
Рассмотрим векторные произведения единичных векторов прямоугольной системы координат. На основании свойства 1 имеем: 
. Из определения векторного произведения следует, что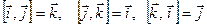 
.
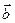Теорема 3.2. Если векторы и в ортонормированном базисе 
имеют координаты 
, то вектор 
имеет координаты: 
.
Доказательство:
1. Разложим векторы и 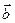по векторам базиса :
, 
.
2. Составим векторное произведение:
[(
), (
)]
Пользуясь свойствами 2, 3, 4 векторного произведения, получим:
Последнее равенство можно записать в виде:
|
|
или
- координаты векторного произведения векторов и 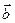в положительно ориентированном базисе.
Координаты векторного произведения векторов и 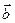в отрицательно ориентированном базисе -
Геометрический смысл векторного произведения.
Теорема 3.3. Абсолютная величина векторного произведения 
равна площади параллелограмма, построенного на этих векторах.
Доказательство:
1. По определению = 
2. S параллелограмма = 
Задача 2: Вычислить площадь и высоту параллелограмма построенного на векторах 
и 
Задача.3: Найти площадь треугольника, если известны координаты его вершин А(1, -2, 3), В(5, 0, -1), С(1, 0, 4)
Физический смысл векторного произведения векторов
Моментом силы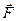 
относительно точки 
называется вектор 
, имеющий начало в точке , направленный перпендикулярно к плоскости, определяемой точкой и вектором силы 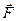. Длина вектора равна произведению длины вектора 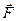на плечо 
( - длина перпендикуляра, опущенного из точки на направление вектора 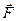), или 
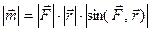, где 
- радиус-вектор точки приложения силы 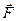. Иначе, 
.
Таким образом, вектор момента силы есть векторное произведение вектора силы и радиус-вектора точки приложения силы.
Определение 3.4. Смешанным (тройным) произведением некомпланарных векторов 
, взятых в определенном порядке, называется скалярное произведение вектора 
и вектора 
Смешанное произведение в ортонормированном базисе.
Теорема 3.5. Если векторы , и 
в ортонормированном базисе имеют координаты , 
то смешанное произведение векторов вычисляется по формуле: 
.
Доказательство.
|
|
1. Выразим координаты вектора в ортонормированном базисе.
По теореме 2.4 лекции 2 имеем: 
.
2. Выразим скалярное произведение векторов и в ортонормированном базисе: 
= 
= = 
.
3. Соберем правую часть равенства в определитель: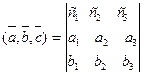 
. Перестановка двух любых строк определителя меняет его знак. Поменяв третью строку со второй, а затем новую вторую с первой, получим: 
.
Свойства смешанного произведения:
1) Если в смешанном произведении два любых вектора равны или коллинеарны, то оно равно нулю;
2) При перестановке местами двух множителей смешанное произведение меняет знак: 
3) При циклической перестановке множителей смешанное произведение не меняется: (
)= 
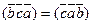(доказательство вытекает из того, что перестановка двух любых строк определителя меняет его знак).
4) Распределительное свойство смешанного произведения: 
5) Сочетательное свойство смешанного произведения при умножении на скаляр: 