ВРЕМЕННОЙ И СПЕКТРАЛЬНЫЙ АНАЛИЗ ПРОХОЖДЕНИЯ
СЛУЧАЙНОГО ПРОЦЕССА ЧЕРЕЗ ЛИНЕЙНЫЕ СИСТЕМЫ
Особенности анализа линейных систем при случайных воздействиях
Линейной системой называют систему, для которой применим принцип суперпозиции, состоящий в том, что отклик системы на сумму воздействий равен сумме откликов на каждое воздействие. Различают линейные системы с сосредоточенными и распределенными, постоянными и переменными параметрами. В дальнейшем для определенности будем рассматривать линейные системы с сосредоточенными постоянными параметрами. Примером такой системы является линейная цепь, составленная из элементов, параметры которых (сопротивление R, индуктивность L, ёмкость С) постоянны.
Основная задача анализа линейной электрической цепи состоит в нахождении отклика y (t) цепи на произвольное воздействие x (t). Связь между x = x (t) и y = y (t) в общем виде устанавливается линейным дифференциальным уравнением n -го порядка
 (4.1)
(4.1)
решение которого при заданных начальных условиях определяет явную функциональную связь между x (t) и y (t). При этом порядок уравнения и величины коэффициентов определяются схемой цепи.
Уравнение (4.1) устанавливает связь между x (t) и y (t) в неявной форме. Чтобы получить явную форму связи, необходимо решить уравнение (4.1) для каждого конкретного воздействия. Эту трудность можно обойти в том смысле, если решить это уравнение один раз для воздействия в виде дельта-функции x (t) =  (t). Полученное решение, в данном случае определяет импульсную характеристику цепи y (t) = h (t).
(t). Полученное решение, в данном случае определяет импульсную характеристику цепи y (t) = h (t).
Дельта-функция обладает фильтрующим свойством:



Пусть имеется некоторая непрерывная функция f (t), тогда
 .
.
Импульсная характеристика h (t) – это отклик линейной цепи при нулевых начальных условиях на воздействие в виде дельта-функции. Зная h (t), можно записать отклик y (t) в виде интеграла свертки h (t) с x (t):
 (4.2)
(4.2)
или в другой форме
 , (4.3)
, (4.3)
где предполагается, что воздействие x (t) подано на вход цепи в момент t = 0, то есть нижний предел интегрирования соответствует моменту подачи входного воздействия, а верхний предел интегрирования t соответствует моменту, при котором ищется отклик y (t), t > 0.
Выражения (4.1), (4.2), (4.3) справедливы в полной мере, если x (t) есть реализация случайного процесса 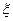 (t). В этом случае эти выражения позволяют найти реализацию y (t) как отклика на конкретную реализацию x (t).
(t). В этом случае эти выражения позволяют найти реализацию y (t) как отклика на конкретную реализацию x (t).
Если же в формулах (4.1), (4.2), (4.3) на место x(t) поставить входной случайный процесс 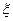 =
= 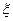 (t), то на выходе, то есть на месте y(t), будет выходной случайный процесс
(t), то на выходе, то есть на месте y(t), будет выходной случайный процесс  =
=  (t). Тогда указанные формулы:
(t). Тогда указанные формулы:
 (4.4)
(4.4)
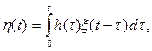 (4.5)
(4.5)
 (4.6)
(4.6)
устанавливают только функциональную связь между 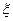 (t) и
(t) и 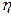 (t). Особенность заключается в том, что эти формулы не могут использоваться для нахождения
(t). Особенность заключается в том, что эти формулы не могут использоваться для нахождения 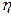 (t), так как
(t), так как 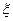 (t) не задаётся конкретной функцией, а представляет собой совокупность реализаций, одна из которых проявляется. Но эти формулы служат для решения основной задачи анализа линейной цепи при случайных воздействиях, заключающейся в нахождении вероятностных характеристик выходного случайного процесса
(t) не задаётся конкретной функцией, а представляет собой совокупность реализаций, одна из которых проявляется. Но эти формулы служат для решения основной задачи анализа линейной цепи при случайных воздействиях, заключающейся в нахождении вероятностных характеристик выходного случайного процесса 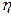 (t), если известны вероятностные характеристики входного случайного воздействия и определена цепь посредством задания порядка и коэффициентов дифференциального уравнения или импульсной характеристики. Так как все зависимости
(t), если известны вероятностные характеристики входного случайного воздействия и определена цепь посредством задания порядка и коэффициентов дифференциального уравнения или импульсной характеристики. Так как все зависимости 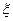 (t),
(t), 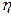 (t), h (t) в формулах (4.4), (4.5), (4.6) заданы во временной области, то анализ цепи с их использованием определяет вероятностный анализ линейных систем во временной области.
(t), h (t) в формулах (4.4), (4.5), (4.6) заданы во временной области, то анализ цепи с их использованием определяет вероятностный анализ линейных систем во временной области.
4.2. Вычисление математического ожидания и корреляционной функции на выходе линейной системы
Пусть линейная цепь задана своей импульсной характеристикой h(t). На вход цепи, начиная с момента времени t = 0, подаётся нестационарный процесс с математическим ожиданием  (t) и корреляционной функцией
(t) и корреляционной функцией  . Требуется найти математическое ожидание
. Требуется найти математическое ожидание  (t) и корреляционную функцию
(t) и корреляционную функцию  выходного процесса
выходного процесса  (рис. 4.1).
(рис. 4.1).
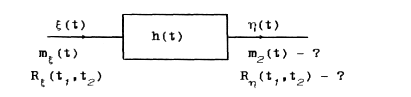
Рис. 4.1
Пусть связь между 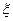 (t) и
(t) и  (t) определяется в соответствии с формулой (4.5) выражением
(t) определяется в соответствии с формулой (4.5) выражением

В этом случае имеем
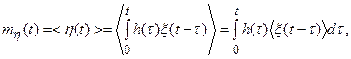
так что
 (4.7)
(4.7)
где символ интегрирования по времени  вынесен за знак оператора математического ожидания <•>, который определяет также интегрирование, но по ансамблю, а интегралы, определяющие интегрирование по различным аргументам, можно менять местами. Кроме того, множитель
вынесен за знак оператора математического ожидания <•>, который определяет также интегрирование, но по ансамблю, а интегралы, определяющие интегрирование по различным аргументам, можно менять местами. Кроме того, множитель 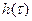 вынесен за оператор <•> как детерминированный. Таким образом, внутри оператора <•> остался только множитель
вынесен за оператор <•> как детерминированный. Таким образом, внутри оператора <•> остался только множитель  , означающий входной случайный процесс, при этом
, означающий входной случайный процесс, при этом 
Из выражения (4.7) следует, что математическое ожидание  (t) определяется в виде формулы интеграла свертки (4.7).
(t) определяется в виде формулы интеграла свертки (4.7).
Если процесс 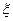 (t) стационарный, то
(t) стационарный, то  (t) =
(t) =  = const и справедливо соотношение
= const и справедливо соотношение
 (4.8)
(4.8)
из которого следует, что  (t) пропорционально переходной характеристике линейной цепи, так как g(t) есть переходная характеристика цепи, определяющая отклик цепи на входное воздействие в виде единичной функции. Если входной процесс имеет
(t) пропорционально переходной характеристике линейной цепи, так как g(t) есть переходная характеристика цепи, определяющая отклик цепи на входное воздействие в виде единичной функции. Если входной процесс имеет  =0, то выходной процесс имеет нулевое математическое ожидание, m=0. Если же m = const и отлично от нуля, то при выполнении условия
=0, то выходной процесс имеет нулевое математическое ожидание, m=0. Если же m = const и отлично от нуля, то при выполнении условия
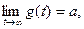 где a = const,
где a = const,
выходной процесс после затухания переходного процесса, вызванного включением стационарного процесса на входе, становится стационарным с математическим ожиданием, равным

Для нахождения  воспользуемся формулой (4.6):
воспользуемся формулой (4.6):
 . (4.9)
. (4.9)
В этом случае связь между  (t) и
(t) и  (t) запишется в виде
(t) запишется в виде
 (4.10)
(4.10)
Из левой и правой части равенства (4.9) вычтем соответственно левую и правую части равенства (4.10). После преобразования получим
 (4.11)
(4.11)
где


В свою очередь, по определению имеем
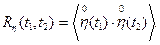 (4.12)
(4.12)
Подставив формулу (4.11) в выражение (4.12) и применив те же приемы, что и при вычислении математического ожидания (4.7), получим

Таким образом, имеем
 (4.13)
(4.13)
где

Из формулы (4.13) следует, что корреляционная функция выходного процесса определяется как двойная свертка между импульсной характеристикой цепи и корреляционной функцией входного процесса.
Если процесс 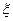 (t) стационарный, для которого
(t) стационарный, для которого

то при t 1 = t и t 2 = t + τ из формулы (4.13) имеем
 (4.14)
(4.14)
Заметим, что R (t, t +  ) зависит от t и t +
) зависит от t и t +  ; даже в случае, если
; даже в случае, если  (t 2 – t 1) зависит только от их разности
(t 2 – t 1) зависит только от их разности  = t 2 – t 1. Из этого следует, что в общем случае при включении на вход стационарного процесса выходной, из-за наличия переходного процесса, является не стационарным.
= t 2 – t 1. Из этого следует, что в общем случае при включении на вход стационарного процесса выходной, из-за наличия переходного процесса, является не стационарным.
При  процесс
процесс  (t) становится стационарным. В этом случае корреляционная функция выходного процесса может быть определена при вычислении предела
(t) становится стационарным. В этом случае корреляционная функция выходного процесса может быть определена при вычислении предела
 (4.15)
(4.15)
Практически выражения (4.8) и (4.15) становятся справедливыми раньше, чем при  , именно после затухания переходных процессов. Например, стационарность выходного процесса по математическому ожиданию в случае цепи первого порядка достигается при
, именно после затухания переходных процессов. Например, стационарность выходного процесса по математическому ожиданию в случае цепи первого порядка достигается при 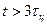 , где
, где  постоянная времени цепи, а по корреляционной функции из-за того, что берется двойная свертка, стационарность процесса достигается в два раза раньше, при
постоянная времени цепи, а по корреляционной функции из-за того, что берется двойная свертка, стационарность процесса достигается в два раза раньше, при 