Искусственный интелект и когнетивная графика

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

Национальный исследовательский ядерный университет

«МИФИ»

 

ИНСТИТУТ ИННОВАЦИОННОГО МЕНЕДЖМЕНТА

КАФЕДРА СИСТЕМНОГО АНАЛИЗА

 

 

Реферат на тему

Искусственный интелект и когнетивная графика

 

Преподаватель: Рыбина Г.В.

Выполнил студент: Михайлов С.А.

Группа: У7-06

Оценка: ________

 

 

Москва 2014

Оглавление.

Введение
1. Когнитивная графика и искусственный интеллект
2. Методы распознавания текста
2.1. Распознавание с помощью метрик
2.2. Распознавание с помощью нейронной сети
2.3. Решающие деревья
3. Методы повышения точности распознавания текста
Заключение
Список литературы

 

Введение.

В настоящее время все документы создаются на компьютерах. Перевод документа из электронной версии в печатную не составляет труда, но перевод из печатной в электронную та ещё проблема, особенно когда документ большой и текста много. Задача перевода информации с печатного на электронный носитель всегда актуальна. Документы, переведенные в электронный вид, существенно облегчают человеку доступ к информации.

Наиболее простой способ перевода печатного документа в электронный вид – сканирование. Результатом сканирования будет изображение, но компьютер не сможет найти на изображении информацию, которую мы ищем. Поэтому необходимо переводить текст на изображении в более удобную форму - текстовое представление информации. Этот вариант имеет ряд плюсов, нежели текст на изображении: снижение затрат на хранение информации, снижение временных затрат на передачу информации, в сети Интернет её легче найти. Поэтому с практической точки зрения этот вариант хранения информации имеет наибольший интерес.

 

1. Когнитивная графика и искусственный интеллект

В искусственном интеллекте термин «когнитивная графика» трактуется как совокупность методов и средств представления знаний и работы с ними на уровне графических (статических и/или динамических) образов. Такие системы предполагают единообразное описание не только графических примитивов, но и сложных графических представлений. Созданные компьютером образы могут рассматриваться как декларативные структуры, трансформирующиеся во внутреннее представление компьютера с помощью процедур, отражающих знания о законах преобразования сформированных образов, и позволяют активизировать представления об объектах, недоступных прямому наблюдению или вообще не имеющих образного представления в обычной реальности.

Установление связи между текстами, описывающими сцены, и соответствующими изображениями потребовало наличия в базах знаний специальных представлений для зрительных образов и процедур соотнесения их с традиционными формами представления знаний.

Графическая информация стала трактоваться с позиций знаний, содержащихся в ней. Если до этого её функция сводилась к иллюстрации тех или иных знаний и решений, то теперь она стала включаться равноправным образом в те когнитивные процессы, которые моделируются в базах знаний и на основе их содержимого. Термин «когнитивная графика» отражает этот принципиальный переход от иллюстрирующих изображений к видеообразам, способствующим решению задач и активно используемых для этого.

Когнитивная функция изображений использовалась в науке и до появления компьютеров. Образные представления, связанные с понятиями граф, дерево, сеть и т.п. помогли доказать немало новых теорем, круги Эйлера позволили визуализировать абстрактное отношение силлогистики Аристотеля, диаграммы Венна сделали наглядными процедуры анализа функций алгебры логики. Систематическое использование когнитивной графики в компьютерах в составе человеко-машинных систем сулит многое. [1]

2. Методы распознавания текста.

2.1. Распознавание с помощью метрик

Пусть Х-произвольное множество. Функция d: X×X → R∪{∞} называется метрикой на Х, если для всех х, y, z ∈ X выполняются следующие условия.

Положительность: d(x, y) > 0, если x≠ y, и d(x, x) = 0.

Симметрия: d(x, y) = d(y, x).

Неравенство треугольника: d(x, z) ≤ d(x, y) + d(y, z). [2]

 

Метрика – некоторое условное значение функции, определяющее положение объекта в пространстве. Таким образом, если два объекта расположены близко друг от друга, то есть похожи, то метрики для таких объектов будут совпадать или быть предельно похожими. Для распознавания в этом режиме была выбрана метрика Хэмминга.

Метрика Хэмминга – метрика которая показывает, как сильно объекты не похожи между собой.
Расстоянием по Хэммингу между двумя q-ичными последовательностями x и y длины n называется число позиций, в которых они различны. [3]

 

Например, возьмем x=10101 и y=01100. Вычислим метрику, сравнивая x и y путем сравнения последовательности. В этом случае метрика Хэмминга равна 3, т.е. эти две последовательности различаются в 3 местах, а именно 10 10 1, 01 10 0.

Следовательно, чтобы определить какая буква изображена нужно найти её метрику.

Чем ближе эта метрика к 0, вернее будет ответ.

 

Но одной лишь метрики не хватит, если буквы схожи между собой. Например такие буквы как «l» «i» схожи, что и приводит к ошибочному распознаванию. Поэтому было принято решение придумать новые метрики, разграничивающие такие буквы в отдельный класс.

Такие буквы как «H» «I» «i» «O» «o» «X» «x» «l» из английского языка, «Ж» «ж» «Н» «н» «О» «о» «Х» «х» из русского языка обладают суперсимметрией, т.е. имеют вертикальные и горизонтальные оси симметрии, поэтому их отнесли в отдельный класс, что позволяет сократить перебор всех метрик.

 

Так же есть такие буквы как «F», которые не имеют осей симметрии, поэтому их можно идентифицировать однозначно. Далее, для каждого класса высчитывается метрика Хэмминга, которая на данном этапе дает лучшие показатели чем при прямом применении.

2.2. Распознавание с помощью нейронной сети

Данные алгоритмы являются попыткой моделирования способности человеческого мышления, в частности, способности обучаться и решать задачи распознавания по прецедентам. Они основаны на достижениях биологии и медицины - простейших моделях человеческого мозга, созданных в середине прошлого века. Биологический мозг рассматривается как множество элементарных элементов - нейронов, соединенных друг с другом многочисленными связями. Нейроны бывают трех типов: рецепторы (принимающие сигналы из внешней среды и передающие другим нейронам), внутренние нейроны (принимающие сигналы от других нейронов, преобразующие их и передающие другим нейронам) и реагирующие нейроны (принимающие сигналы от нейронов и вырабатывающие сигналы во внешнюю среду).

Простейшая и наиболее распространенная модель человеческого мозга, ориентированная на решение задач распознавания – искусственная многослойная нейронная сеть.

Элементарной ячейкой нейронной сети является модель искусственного нейрона (рис. 1).

x2

x1

x3

xN

Вход

…

w2

w1

w3

wN

Z

Выход y=f(Z)

Рис. 1. Модель искусственного нейрона

Каждый внутренний или реагирующий нейрон имеет множество входных связей (синапсов), по которым поступают сигналы от других внутренних нейронов или рецепторов, и одну выходящую связь (аксон). Каждая связь имеет некоторый «вес» . При поступлении на вход нейрона совокупности сигналов они «усиливаются» с соответствующими весами . Нейрон переходит в состояние, числовая оценка которого вычисляется как 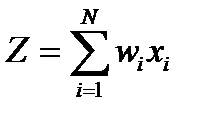. Величина выходного сигнала вычисляется как , где - активационная функция. Примеры активационных функций приведены на рис. 2-5.

 

y x	y x
Рис. 2. Функция единичного скачка	Рис. 3. Единичный скачок с линейным порогом
y x -1	y x
Рис. 4. Гиперболический тангенс f(x)=th(x)	Рис.5. Функция сигмоида f(x)=1/(1+exp(-ax))

Нейрон считается «возбужденным», если выходной сигнал отличен от нуля, а величина характеризует степень возбуждения. Вид функций и область их изменения отражают априорные представления о функционировании биологических нейронов: величина возбуждения зависит монотонно от состояния, ограничена снизу и сверху, и «сильно» меняется в небольшом интервале значений .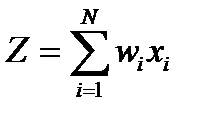

Наиболее простыми, распространенными и исследованными являются многослойные нейронные сети прямого действия. Общий вид подобной сети изображен на рис. 6. Сеть состоит из N слоев, каждые слой состоит из нейронов, каждый нейрон j-го уровня связан с каждым нейроном j+1 – го уровня. Фиктивный нулевой слой состоит из n входных нейронов, на каждый из которых подается значение некоторого признака . Результатами классификации являются выходные значения нейронов N -го слоя.

Распознаваемый объект S поступает на 0-й слой. Далее поступивший сигнал (признаковое описание) последовательно преобразуется по слоям согласно заданным фиксированным весам синаптических связей и выбранной активационной функции. Если есть значение j-го нейрона выходного слоя, то информационный вектор результатов классификации S вычисляется согласно (1.1)

(1.1)

x1

x2

x3

xn

y1N

…

…

…

…

ylN

y2N

0-й слой

N-й слой

i-й слой

i+1-й слой

Рис.6. Структурная схема нейронной классифицирующей сети прямого действия

Значения неизвестных весовых коэффициентов находятся в результате процесса обучения сети. Начальные значения весовых коэффициентов задаются случайно. Объекты обучения последовательно поступают на вход сети. Если предъявленный объект классифицируется правильно, коэффициенты остаются прежними и на вход сети поступает следующий объект. Если при классификации объекта происходит ошибка, весовые коэффициенты изменяются определенным образом. Для однослойной сети они меняются согласно простой итерационной формуле подобно используемой в методе потенциальных функций. Для многослойной сети используются специальные рекуррентные формулы пересчета весовых коэффициентов от последнего уровня до первого (метод «обратного распространения ошибки»). Обучение заканчивается, если изменение коэффициентов не приводит к дальнейшему уменьшению суммарного числа ошибок на обучающей выборке. [4]

2.3. Решающие деревья

Методы распознавания, основанные на построении решающих деревьев, относятся к типу логических методов. В данном классе алгоритмов распознавание объекта осуществляется как прохождение по бинарному дереву из корня в некоторую висячую вершину. В каждой вершине вычисляется определенная логическая функция. В зависимости от полученного значения функции происходит переход далее по дереву в левую или правую вершину следующего уровня. Каждая висячая вершина связана с одним из классов, в который и относится распознаваемый объект, если путь по дереву заканчивается в данной вершине.

Бинарным корневым деревом (БД) называется дерево, имеющее следующие свойства:

а) каждая вершина (кроме корневой) имеет одну входящую дугу;

б) каждая вершина имеет имеет либо две, либо ни одной выходящей дуги.

Вершины, имеющие две выходящие дуги, называются внутренними, а остальные – терминальными или листьями.

Пусть задано N предикатов 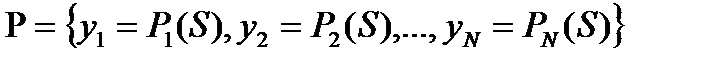, определенных на множестве допустимых признаковых описаний {S}, именуемые признаковыми предикатами. Каждый предикат отвечает на вопрос, выполняется ли некоторое свойство на объекте S или нет. Примерами признаковых предикатов могут быть

Каждой строке 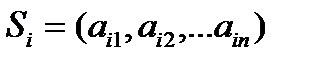таблицы обучения поставим в соответствие бинарную строку значений предикатов на описании . В результате, таблице будет соответствовать бинарная таблица бинарных «вторичных описаний» объектов обучения.

Бинарное дерево называется решающим, если выполнены следующие условия:

1. каждая внутренняя вершина помечена признаковым предикатом из ;
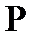2. выходящие из вершин дуги помечены значениями, принимаемыми предикатами в вершине;
3. концевые вершины помечены метками классов;
4. ни в одной ветви дерева нет двух одинаковых вершин.

Пример подобного дерева для конфигурации из трех классов (рис.7) приведен на рис. 8.

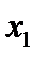
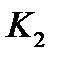
Рис. 7. Конфигурация объектов трех классов. Объекты классов обозначены, соответственно, символами , O, D

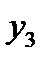
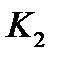
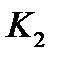
0

Рис.8. Решающее дерево для классов рис. 7

На рис.8 приведено некоторое решающее дерево, позволяющее правильно распознавать объекты трех классов, изображенных на рис.7. Вершины дерева помечены следующими предикатами: Данному решающему дереву соответствуют характеристические функции классов , , , принимающие значение 1 на объектах «своего» класса и 0 на объектах остальных классов.

Приведем еще один пример решающего дерева (рис.9), построенного непосредственно по таблице обучения: 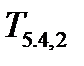= . (1.2)

В качестве признаковых предикатов используются

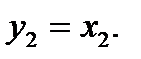
0

0

Рис.9. Решающее дерево бинарной таблицы обучения (1.2)

Здесь в качестве приближений для характеристических функций классов выбраны функции , . В данном примере, для построения решающего дерева использованы только два признака.

Задача построения решающего дерева по обучающим данным решается неоднозначно, методам построения решающих деревьев посвящена обширная литература.[4]

3. Методы повышения точности распознавания текста.

Одним из широко используемых методов повышения точности распознавания является одновременное использование нескольких различных распознающих модулей и последующее объединение полученных результатов (например, путем голосования). При этом очень важно, чтобы алгоритмы, используемые этими модулями, были как можно более независимы. Это может достигаться как за счет использования распознающих модулей, использующих принципиально различные алгоритмы распознавания, так и специальным подбором обучающих данных. [6,7]

Один из таких методов был предложен несколько лет назад и основан на использовании трех распознающих модулей (машин). В первую очередь необходимо создать библиотеку эталонных векторов признаков. Для этого на стадии обучения вводят в систему OCR большое количество образцов начертания символов, позже может появиться необходимость расширить базу знаний. Для каждого образца система выделяет признаки и сохраняет их в виде соответствующего вектора признаков. Набор векторов признаков, описывающих символ, называется классом или кластером. [6,7]

Определяем кластер к каждому символу. Правдоподобие получаемого результата зависит от выбранной метрики пространства признаков. К наиболее известным метрикам относится Евклидово расстояние:

,

где - i-й признак из j-го эталонного вектора; - i-й признак тестируемого изображения символа.

Одна из методик, позволяющих улучшить метрику сходства, основана на статистическом анализе эталонного набора признаков. При этом в процессе классификации более надежным признакам отдается больший приоритет:

,

где w_i, - вес i-го признака. [5]

Итак, первая машина начинает обучение обычным образом. Вторая обучается на результатах первой машины. Третья машина обучается на символах, которые различно распознали первая и вторая машины.

Далее распознаваемые символы подаются на вход всем трем машинам. Оценки, получаемые на выходе всех трех машин складываются. Символ, получивший наибольшую суммарную оценку выдается в качестве результата распознавания.

Заключение.

Использование когнитивной графики в искусственном интеллекте очень масштабно: помимо распознавания текста сюда можно включить распознавание изображений, распознавание лиц и другие графические образы.

Один из самых распространенных методов распознавания – нейронные сети. Этот метод позволяет не просто распознавать текст, а обучаться машине, что позволяет более качественно распознавать текст в дальнейшем.

 

Список литературы

1. Ю.В. Арбузов, Е.А. Ахромушкин, А.В. Беляков, В.Б. Глаголев, А.А. Грушо, Т.И. Гусева, М.С. Заботнев, А.И. Евсеев, А.Л. Конин, И.М. Крепков, Ю.М. Кузнецов, В.П. Кулагин, В.М. Линьков, Б.Р. Липай, С.И. Маслов, В.Ф. Очков, А.Н. Савкин, А.Н. Седов, А.Ю. Семенов, А.Н. Симонов, Т.М. Скворцова, И.В. Станкевич, А.А. Сутченков, А.И. Тихонов, М.Б. Федоров. Информатизация образования: направления, средства, технологии: Пособие для системы повышения квалификации / Под общ. ред. С.И. Маслова. —М.: Издательство МЭИ, 2004. — 868 с.

2. Dmitri Burago, Yuri Burago, Sergei Ivanov. A Course in Metric Geometry. —American Mathematical Society Providence, Rhode Island, 2001. — 489 с.

3. Блейхут Р. Теория и практика кодов, контролирующих ошибки. — М.: Мир, 1986. — 576 с.

4. Журавлев Ю.И., Рязанов В.В., Сенько О.В. Распознавание. Математические методы. Программная система. Практические применения. —М: Фазис, 2005. —159 с.

5. Бондаренко А.В., Галактионов В.А., Горемычкин В.И., Ермаков А.В., Желтов С.Ю. Исследование подходов к построению систем автоматического считывания символьной информации. — М: ИПМ им. М.В.Келдыша РАН, 2003. —15 с.

6. Robert E. Schapire, "The strength ofweak learnability". Machine Learning, 5(2): 197-227, 1990.

7. H.Drucker, R.Schapire, P.Simard. “Boosting Performance in Neural Networks.” International Journal of Pattern Recognition and Artificial Intelligence. 7 705-720, 1993.

8. Аникин И. В., Шагиахметов М. В. Методы нечеткой обработки, распознавания и анализа изображений // Распознавание образов и анализ изображений: 6-ая Междунар. конф. 21-26 октября 2002. — Новгород, 2002. — С. 16-21.

9. Пытьев Ю. П., Чуличнов А. И. Морфологический анализ изображений: принципы и применение // Распознавание образов и анализ изображений: 6-ая Междунар. конф. 21-26 октября 2002. — Новгород, 2002. — С. 464-469.

10. Большакова Е.И., Васильева Н.Э., Морозов С.С. Лексико-синтаксические шаблоны для автоматического анализа научно-технических текстов. //Десятая национальная конференция по искусственному интеллекту с международным участием КИИ-2006 (25-28 сентября 2006 г., Обнинск): Труды конференции. В 3-т., М: Физматлит, 2006

11. Карпов В.Э. Об одной псевдоассоциативной модели текста, М:, 2009 (doc)

12. Рубашкин В.Ш. Семантический компонент в системах понимания текста. //Десятая национальная конференция по искусственному интеллекту с международным участием КИИ-2006 (25-28 сентября 2006 г., Обнинск): Труды конференции. В 3-т., М: Физматлит, 2006

13. Хорошевский В.Ф. Оценка систем извлечения информации из текстов на естественном языке: кто виноват, что делать. //Десятая национальная конференция по искусственному интеллекту с международным участием КИИ-2006 (25-28 сентября 2006 г., Обнинск): Труды конференции. В 3-т., М: Физматлит, 2006

14. Поспелов Д.А. Десять "горячих точек" в исследованиях по искусственному интеллекту //Интеллектуальные системы (МГУ). - Т.1, вып.1-4., 1996, с.47-56