Рассмотрим две аффинные системы координат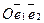 
и 
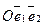. Назовем
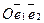- старой системой координат; 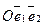- новой системой координат
Задача преобразования координат сводится к тому, что зная координаты нового начала и новых координат векторов в старой системе, выразить координаты 
некоторой точки М в старой системе через координаты 
этой же точки в новой системе.
Дано: 
- в системе координат ;
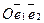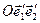- в системе координат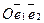 
;
- в системе координат ;
- в системе координат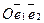
Выразить: координаты точки в старой системе через ее координаты в новой системе.
Решение:
1 случай: Пусть системы отличаются и координатными векторами, и началом координат.
1. По правилу треугольника сложения векторов, имеем: 
(*)
2. Разложим векторы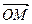 
, 
, 
и 
по базису 
и 
:
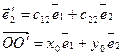
3. Выразим вектор 
через и : 
4. Подставим в равенство (*) все выражения из 2) и 
Так как 
и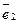 
не коллинеарны, то получаем
Таким образом,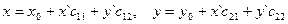 
- формулы преобразования аффинных координат.
2 случай:
Пусть системы отличаются только началом.
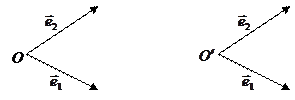O 
O`
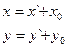
3 случай:
Пусть системы координат отличаются координатными векторами
Формулы преобразования аффинной системы координат примут вид:
Преобразования прямоугольной декартовой системы координат.
Так как прямоугольная декартова система координат является частным случаем аффинной системы координат, то формулы преобразования имеют тот же вид, но, в зависимости от ориентации систем, на них накладываются некоторые условия.
1) Пусть системы 
и 
одинаково ориентированы и на них задана положительная ориентация.
Пусть 
тогда 
. На ориентированной плоскости справедливы следующие равенства:
Таким образом, формулы преобразования аффинных координат принимают вид: 
Действительно, 
, значит, системы одинаково ориентированы, что не противоречит условию.
2) Системы одинаково ориентированы, но отличаются началом:
3) Системы одинаково ориентированы, но отличаются базисом, начала
координат совпадают.
4) Системы ориентированы противоположно
Пусть тогда . Тогда справедливы следующие равенства: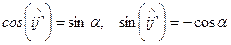 
Формулы преобразования примут вид:
Действительно, 
, значит системы ориентированы противоположно
Задания по содержанию лекции
Задание 1. Провести аналогию тем «Координаты на плоскости» и «Координаты в пространстве», заполнив таблицу.
| Основные вопросы | Координаты на плоскости | Координаты в пространстве |
| Прямоугольная система координат | ||
| Аффинная система координат | ||
| Координаты точки | ||
| Разложение радиус-вектора точки по базисным векторам | ||
| Расстояние между точками | ||
| Координаты точки, делящей отрезок в данном отношении | ||
| Координаты середины отрезка | ||
| Преобразование аффинных координат | ||
| Преобразование прямоугольных координат |
2. Нарисуйте фигуру, которая в данной прямоугольной системе координат задается следующим образом:
o 
,
o 
,
o 
,
o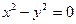 
,
o 
,
o 
,
o 
,
o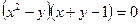 
,
o 
,
o 
,
o 
,
o 
o 
2. Найти координаты образа и прообраза точки 
, зная формулы преобразования координат: 
.
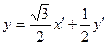