Лекция №4
Аффинные системы координат на плоскости и в пространстве. Основные задачи в координатах. Прямоугольные системы координат на плоскости и в пространстве.
Ориентация плоскости. Преобразования аффинных и прямоугольных координат
Цели: Ввести определения аффинной и прямоугольной систем координат на плоскости и в пространстве; рассмотреть основные задачи в координатах для аффинной системы координат и прямоугольной системы координат; обзорно познакомить с ориентацией плоскости и пространства. Вывести формулы преобразования координат для аффинных и прямоугольных координат.
План лекции:
1. Понятие аффинной системы координат на плоскости.
2. Основные задачи в аффинных координатах.
3. Понятие прямоугольной системы координат.
4. Основные задачи в прямоугольных координатах.
5. Ориентация плоскости и пространства.
6. преобразование аффинных и прямоугольных координат.
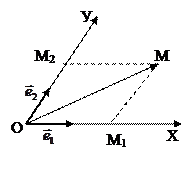Определение 4.1. Тройка, состоящая из точки О и базиса 
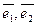называется аффинной системой координат 
.
Точка О – начало координат, а векторы 
и - координатными векторами. Направленные прямые, проходящие через начало координат и параллельные координатным векторам, на которых положительные направления определяются этими векторами, называются осями координат. Ось координат, на которой положительное направление определяется вектором , называется осью абсцисс и обозначается 
, вектором - осью ординат и обозначается 
.
Пусть - аффинная система координат, а М – произвольная точка плоскости.
Вектор 
называется радиус-вектором точки М (относительно точки О). Координаты 
и 
вектора 
в базисе 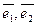называются координатами точки М в системе координат . Число называется абсциссой точки М, а число - ординатой точки М; пишут 
. Таким образом, координатами точки М в системе называются числа и такие, что 
.
Чтобы построить точку М по данным координатам и в системе координат надо:
1. На оси построить точку 
, на оси - точку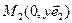 
;
2. Через точки 
и 
провести прямые, параллельные соответственно осям и ;
3. Точка пересечения прямых – искомая точка .
Задача 1.
В аффинной системе координат даны две точки 
и 
. Найти координаты вектора 
.
Решение.
1. 
.
2. Векторы 
- радиус-векторы точек и , значит, векторы имеют координаты: 
, 
.
3. По свойству координат имеем, что вектор как разность векторов имеет координаты: 
.
Итак, каждая координата вектора равна разности соответствующих координат конца и начала вектора.
Деление отрезка в данном отношении.
Пусть и - две точки плоскости, а 
- некоторое действительное число, причем 
. Говорят, что точка 
делит направленный отрезок 
в данном отношении , если 
. Из данного равенства следует:
o 
, то 
и лежит внутри отрезка ;
o 
, то 
и лежит вне отрезка .
Задача 2
В аффинной системе координат отрезок 
задан координатами своих концов: 
, 
. Найти координаты точки , делящей отрезок в отношении .
Решение.
1. Выразим векторы: 
и 
;
2. Равенство примет вид: 
;
Выразим : 
(*).
3. Векторы 
- радиус-векторы точек , , , поэтому эти векторы в базисе 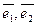имеют координаты: 
, 
и 
;
4. Применив к равенству (*) свойства координат векторов имеем формулы для нахождения координат точки , делящей отрезок в отношении :
Для нахождения координат середины отрезка 
формулы преобразовываются следующим образом: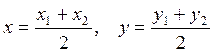 
Определение 4.2. Система координат называется прямоугольной декартовой или просто прямоугольной, если его координатные векторы являются единичными взаимно перпендикулярными векторами.
Такая система координат с началом в точке О обозначается: 
или 
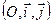, где 
.
Координаты точки в прямоугольной системе координат имеют простой геометрический смысл.
Точки и проекции точки М на
оси координат.
Таким образом, 
, если -
точка положительной полуоси ;
, если - точка отрицательной полуоси ; 
, если совпадает с началом координат.
Аналогичный геометрический смысл имеет и ордината у точки . Итак понятие координат в прямоугольной системе координат совпадает с тем понятием, которое известно из курсов алгебры и геометрии средней школы.
Длина отрезка в прямоугольной системе координат.
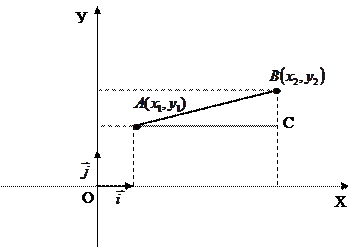
1. Пусть в прямоугольной системе координат точки 
имеют координаты 
и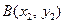 
.
2. По определению длины вектора 
, где 
3. 
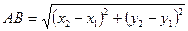
Ориентация плоскости
Пусть L - некоторое множество векторов плоскости. Выделим в этом множестве два базиса 
Выразим векторы второго базиса через векторы первого.
, где 
Матрица перехода от базиса А к базису В имеет вид: 
, 
- определитель второго порядка матрицы перехода от базиса А к базису В.
Определение 4.3. Базисы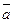 
и 
называются одинаково ориентированными, если определитель А|В больше 0.
Обозначается: A 
B (базис 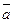одинаково ориентирован с базисом )
Определение 4.4. Одинаково ориентированные базисы 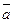и из множества всех базисов подпространства L называются ориентацией векторного подпространства L.
Одна из ориентаций называется положительной, другая – отрицательной.
Определение 4.5. Векторное подпространство L называется ориентированным, если в нем выбрана положительная ориентация.
Определение 4.6. Базисы положительной ориентации называются правыми, отрицательной ориентации – левыми.
Определение 4.7. Плоскость называется ориентированной, если ориентированы подпространства векторов этой плоскости.
Определение 4.8. Система координат называется правой, если базис – правый. Левой, если базис – левый.
Рассмотрим два вектора 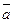и – ненулевые и заданные в определенном порядке.
 |