СЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ ПЛОСКОСТЬЮ

В заданиях на построение усечен­ных геометрических тел можно выде­лить следующие задачи: 1) построе­ние усеченного тела в системе трех плоскостей проекций; 2) определение истинной величины фигуры сечения; 3) построение развертки усеченного тела и 4) вычерчивание его аксоно­метрической проекции. Ниже помеще­ны рекомендации по решению каждой из перечисленных задач.

Вначале по положению секущей плоскости определяют вид фигуры се­чения и в зависимости от формы гео­метрического тела выбирают прием построения проекций сечения. В зада­ниях секущие плоскости занимают проецирующее положение, поэтому одна проекция сечения задается. Не­достающие проекции фигуры сечения призмы или пирамиды строят по точ­кам пересечения их ребер с заданной плоскостью. Если же плоскость пере­секает поверхность вращения по ле­кальной кривой, то начинают с определения ее характерных точек.

Например, фронтально проецирующая плоскость Р (рис. 106) пересекает цилиндр по не­полному эллипсу. Его характерными точками являются: 1) А и В — точки, принадлежащие линии пересечения плоскости Р с основанием цилиндра; 2) С — конец большой оси эллипса; 3) D и Е — концы малой оси эллипса и они же точки, лежащие на очерковых образующих ци­линдра Последовательность нахождения точек эллипса указана стрелками на примере проме­жуточных точек 1 и 2.

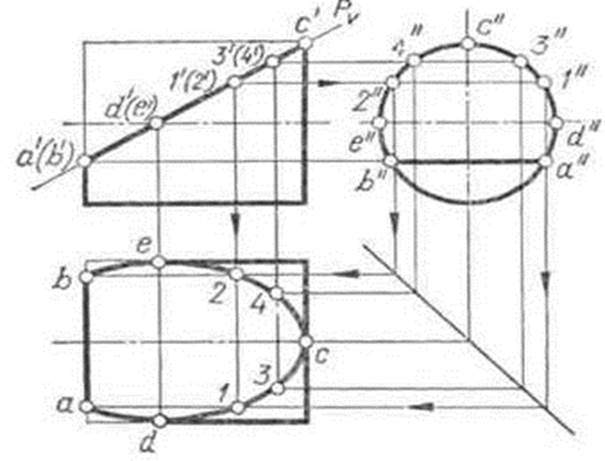
Рис.1

Истинную величину фигуры сече­ния определяют с помощью способа перемены плоскостей проекций или вращения. Если применяют способ перемены плоскостей проекций, то дополнительную плоскость задают параллельно секущей плоскости. Дополнительную плоскость совмещают с основной плоскостью проекций так, чтобы новая проекция сечения не наложилась на имеющиеся проекции. При использовании способа вращения ось вращения целесообразно распола­гать в секущей плоскости и на неко­тором расстоянии от тела.

Для примера показано положение оси вра­щения U (рис. 1) при определении истинной величины сечения четырехугольной призмы фронтально проецирующей плоскостью Р.

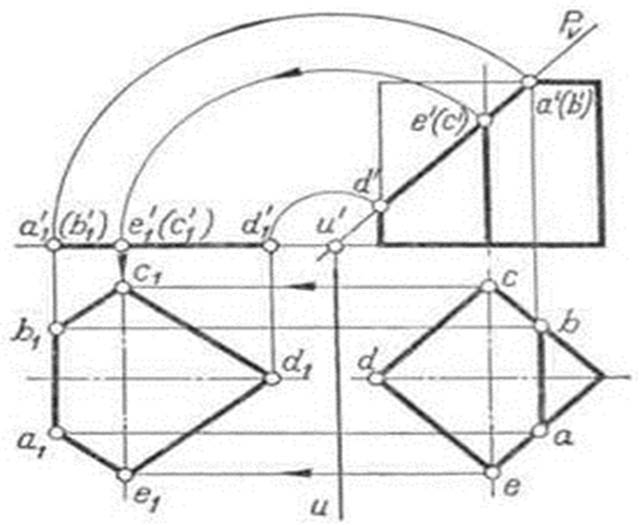
Рис.2

Построение развертки усеченного тела начинают с вычерчивания раз­вертки его полной боковой поверхно­сти. Далее на нее наносят линии се­чения и пристраивают к ней остальные части развертки — основания и фигуру сечения. Если какие-либо элементы, необходимые для построения разверт­ки, на проекциях искажены, то пред­варительно определяют их истинную величину.

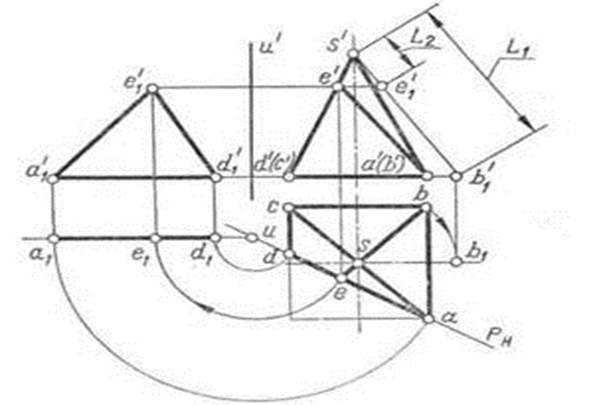
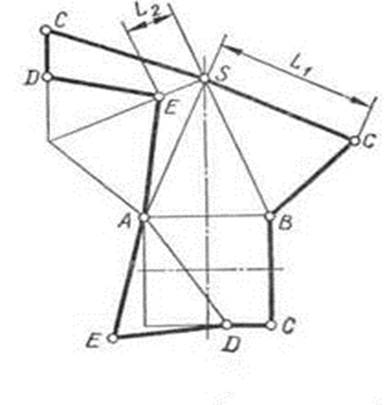
Рис.3

Например, для построения развертки пра­вильной усеченной четырехугольной пирамиды (рис. 3) необходимо определить истинную ве­личину фигуры сечения — треугольника ADE и длину одного из ее боковых ребер, например ребра SB. Для определения истинной величины этих элементов их поворачивают до положения, параллельного плоскости V. Треугольник ADE повер­нут вокруг оси U, а ребро SB — вокруг высо­ты пирамиды. Далее строят развертку согласно рекомендациям в следующем порядке: задают положение вершины S; вычерчивают развертку полной боковой поверхности пирамиды; наносят на нее линии сечения DE и AE с помощью от­резков SE = = s^′e′₁ = L₂ и DC = dc; пристраивают к ребру основания АВ фигуру усеченного основания— четырехугольник ABCD = abcd и к его стороне AD — треугольник ADE = a′₁e′₁ d′₁.

Усеченные тела на аксонометриче­ской проекции вначале вычерчивают целыми. Далее изображают проекцию сечения и контурными линиями обво­дят усеченную часть тела

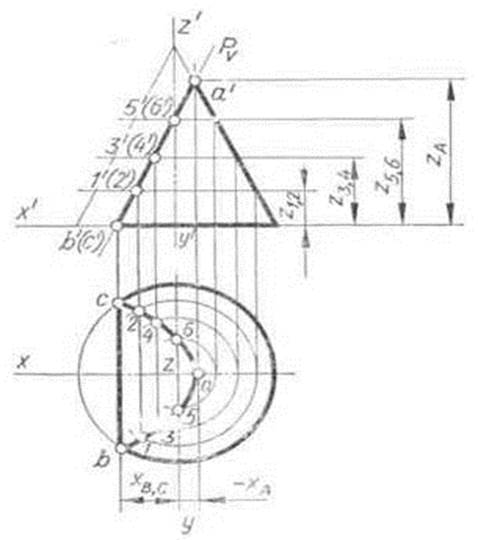
Рис.4

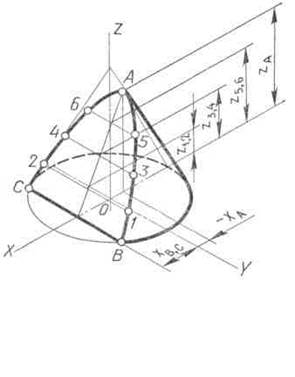рис.5

Для примера на рис. 5++ вычерчена изо­метрическая проекция конуса, усеченного фронтально проецирующей плоскостью Р по параболе. Параболу на изометрической проекции начинают строить с ее вершины А. Эту точку получают с помощью координаты— х_А. Проекции нижних точек параболы В и С строят по координате х_{В, С}. Соединив точку А с серединой отрезка ВС, получают проек­цию оси симметрии параболы. Для построе­ния ее промежуточных точек откладывают по оси конуса от его основания отрезки, равные координатам z_1,2, z_3,1, z_5,6. Через концы от­ложенных отрезков проводят прямые, па­раллельные оси координат X, до пересечения с осью симметрии параболы. Через получен­ные точки проводят хорды параболы, которые параллельны ее нижней хорде ВС. Длину каждой хорды замеряют на горизонтальной проекции усеченного конуса и откладывают на соответствующей хорде изометрической проекции.

 

 

Построение чертежей разверток
Для изготовления многих изделий из листового материала необходимо выполнить ихразвертки. Развертываемыми поверхностями называются такие поверхности, которые могут быть совмещены всеми своими точками с плоскостью без образования складок и разрывов. Рассмотрим процесс построения разверток некоторых многогранников и кривых поверхностей (рис. 125).

 

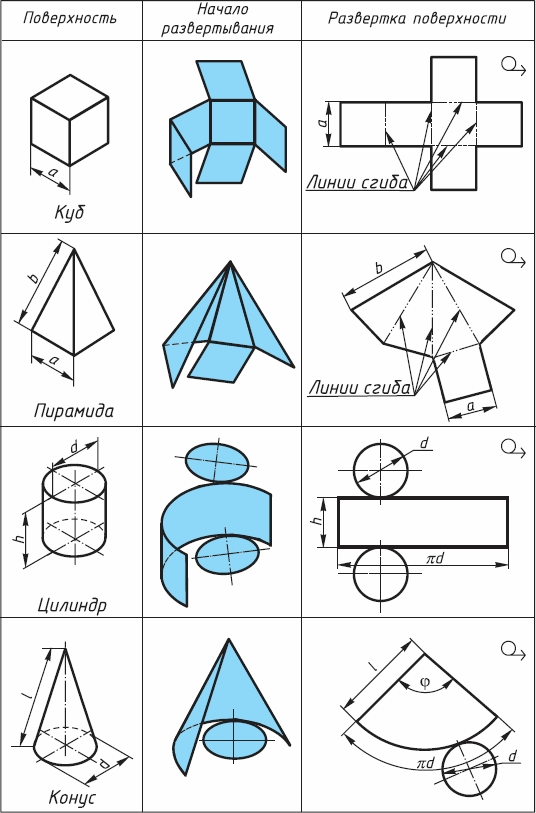
Рис. 125

Развертка поверхности любой прямой призмы, в том числе и куба, представляет собой плоскую фигуру, составленную из боковых граней - прямоугольников и двух оснований - многоугольников. Развертка пирамиды состоит из треугольников (их число равно числу граней пирамиды) и многоугольника основания.
Развертка поверхности цилиндра состоит из прямоугольника и двух кругов. Одна сторона прямоугольника равна высоте цилиндра, другая -длине окружности основания. На чертеже к прямоугольнику пристраиваются два круга, диаметр которых равен диаметру оснований цилиндра.
Развертка поверхностей конуса представляет собой плоскую фигуру, состоящую из сектора - развертки боковой поверхности и круга - основания конуса.

Угол φ можно вычислить и по формуле:

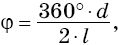
где d — диаметр окружности основания; I - длина образующей конуса. На чертеже развертки над изображением ставят специальный знак. От линий сгиба, где они есть (а их проводят штрихпунктирной с двумя точками), проводят линии-выноски и пишут на полке «Линии сгиба». Выполнить комплексный чертёж конуса https://www.youtube.com/watch?v=SSsuZWf55IA и цилиндра https://www.youtube.com/watch?v=rOy71vfdAlY https://www.youtube.com/watch?v=nheqP8C8hsc

после просмотра видео.

 

Формат должен быть ограничен рамкой. Рамка чертится на каждом листе чертежа, включая титульный лист. Отступ рамки от края формата слева 20 мм., справа, снизу и сверху – 5 мм. В правом нижнем углу чертежа помещается основная надпись. Пример основной надписи приведен на рисунке 6.1.

 

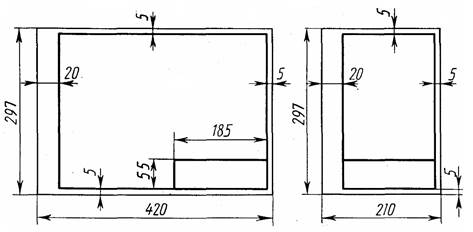
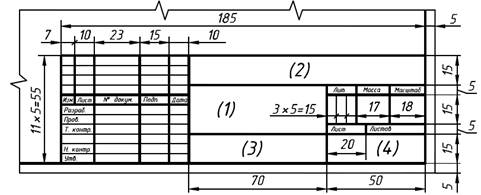Рис.6 Расположение основной надписи на листе

 

Рис. 6.1 Размеры основной надписи

В соответствии с ГОСТ 2.104-2006 на всех конструкторских документах (как чертежах, таки текстовых документах, пояснительных записках и т.п.) применяется одна из трех форм основных надписей. Основные надписи выполняются линиями по ГОСТ 2.303-68.

На рис. 6.1 приведена форма и размеры основной надписи, применяемой для чертежей и схем (форма 1). В графах основной надписи (номера граф на формах показаны в скобках) указывают:

в графе 1 – наименование изделия в именительном падеже в единственном числе (например, «деталь»);

в графе 2 – обозначение документа по ГОСТ 2.201-80. Для учебных чертежей рекомендуется следующая структура обозначений:

ОП 131. 03. 09. 00. 001

где ОП 131 – номер группы, 03 – номер задания, 09 – номер варианта, 00 – номер узла, 001 – номер детали (работы);

в графе 3 – обозначение материала детали (заполняют только на чертежах деталей);

в графе 4 – наименование предприятия (учебного заведения и кафедры);

в графе лист – порядковый номер листа, если лист один, то графу не заполняют;

в графе листов – общее количество листов документа. Графа заполняется только на первом листе;

в графе масштаб – масштаб изображения (например, 1:1);

в графе разработал – фамилия студента;

в графе проверил – фамилия преподавателя, принявшего чертеж.

Задания к чертежам берутся в соответствии со своим вариантом из таблиц.

Изображения равномерно размещаются в пределах формата чертежа. Все надписи, как и отдельные обозначения в виде букв и цифр на чертеже, должны быть выполнены стандартным шрифтом размером 5 мм в соответствии с ГОСТ2.304-81. Чертежи выполняются с помощью чертежных инструментов.

 

ЗАДАНИЕ: Работу выполнить в соответствии

своего варианта(взять последнюю цифру номера из зачётной книжки студента)

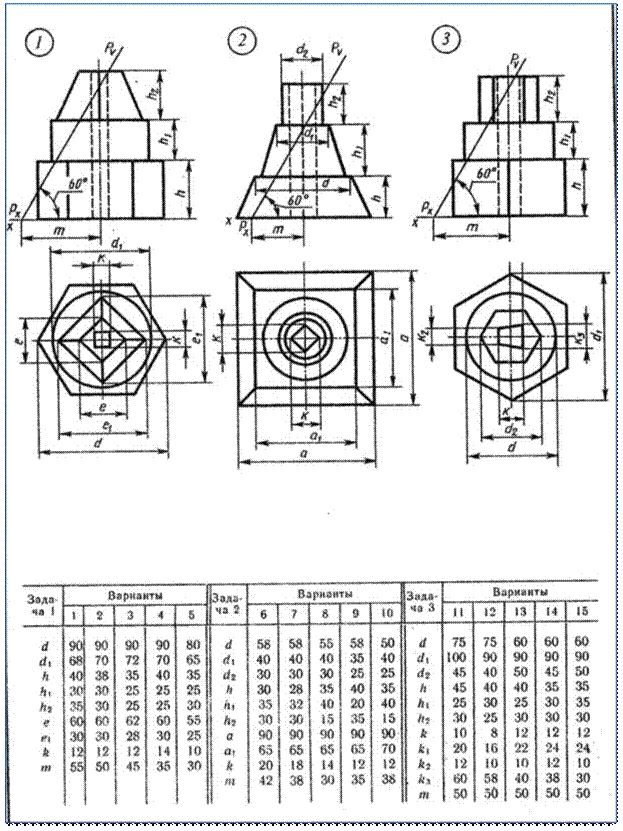
Графическая работа №5(1 часть). «Усечённая призма».

Перечертить данный образец на формат А3.

Нанести размеры на чертеже по образцу.

Оформить чертёж (выполнить рамку и основную надпись).

Задание состоит из четырёх последовательных построений:

1. Выполнение трёх видов усечённого геометрического тела

2. Нахождение натуральной величины фигуры сечения способом поворота секущей плоскости

3. Построение изометрической проекции усечённого геометрического тела

4. Построение развёртки поверхности усечённого геометрического тела

 

 

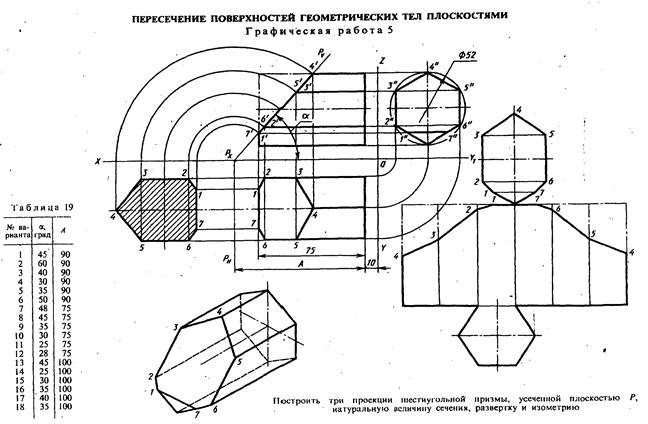
Образец выполнения графической работы №5(1 часть)

 

 

ЗАДАНИЕ: Работу выполнить в соответствии своего варианта(взять последнюю цифру номера из зачётной книжки студента)

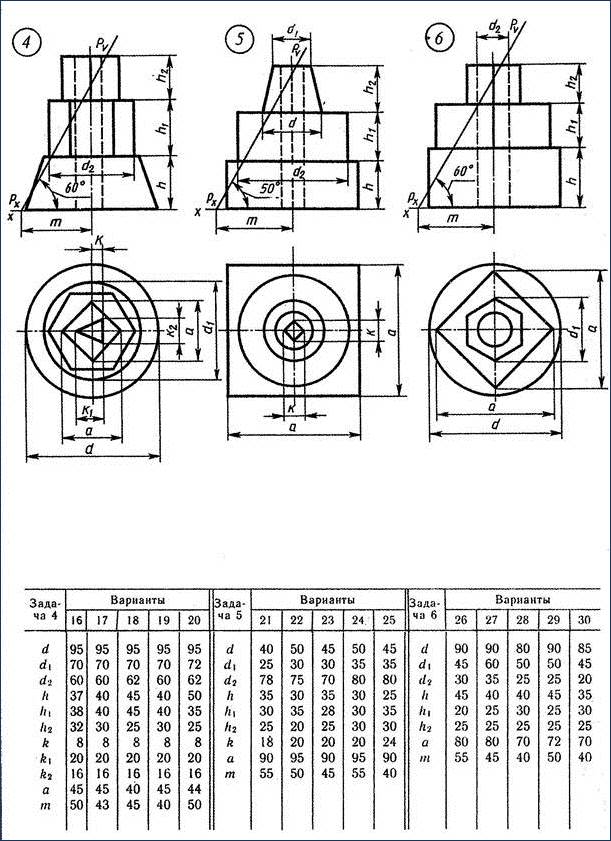
Графическая работа №5(2 часть). «Усечённая пирамида».

Перечертить данный образец на формат А3.

Нанести размеры на чертеже по образцу.

Оформить чертёж (выполнить рамку и основную надпись).

Задание состоит из четырёх последовательных построений:

1. Выполнение трёх видов усечённого геометрического тела

2. Нахождение натуральной величины фигуры сечения способом поворота секущей плоскости

3. Построение изометрической проекции усечённого геометрического тела

4. Построение развёртки поверхности усечённого геометрического тела

 

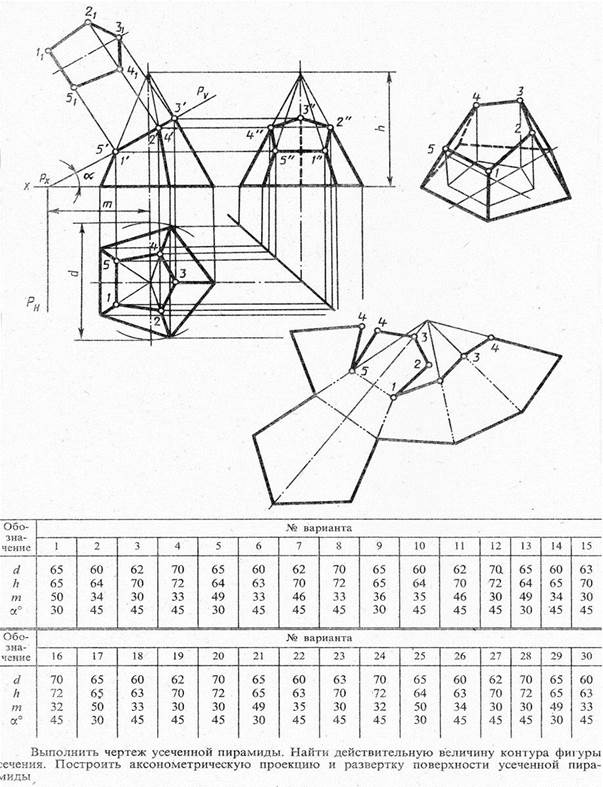
Образец выполнения графической работы №5(2 часть)

 

ЗАДАНИЕ: Работу выполнить в соответствии своего варианта(взять последнюю цифру номера из зачётной книжки студента)

Графическая работа №6(1 часть). «Усечённый конус».

Перечертить данный образец на формат А3

Нанести размеры на чертеже по образцу.

Оформить чертёж (выполнить рамку и основную надпись).

Задание состоит из четырёх последовательных построений:

1. Выполнение трёх видов усечённого геометрического тела

2. Нахождение натуральной величины фигуры сечения способом поворота секущей плоскости

3. Построение изометрической проекции усечённого геометрического тела

4. Построение развёртки поверхности усечённого геометрического тела

 

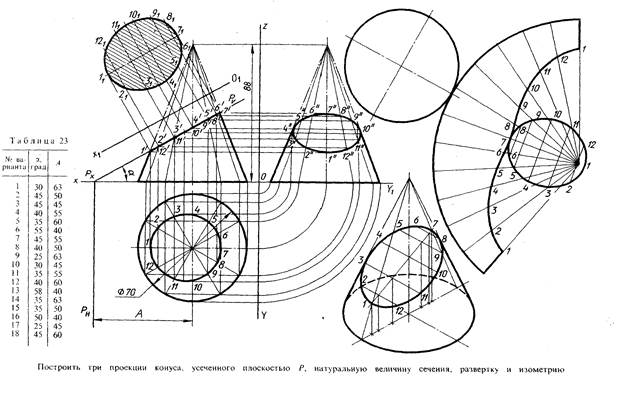
Образец выполнения графической работы №6(1 часть)

 

ЗАДАНИЕ: Работу выполнить в соответствии своего варианта(взять последнюю цифру номера из зачётной книжки студента)

Графическая работа №6(2 часть). «Усечённый цилиндр».

Перечертить данный образец на формат А3.

Нанести размеры на чертеже по образцу.

Оформить чертёж (выполнить рамку и основную надпись).

Задание состоит из четырёх последовательных построений:

1. Выполнение трёх видов усечённого геометрического тела

2. Нахождение натуральной величины фигуры сечения способом поворота секущей плоскости

3. Построение изометрической проекции усечённого геометрического тела

4. Построение развёртки поверхности усечённого геометрического тела

 

 

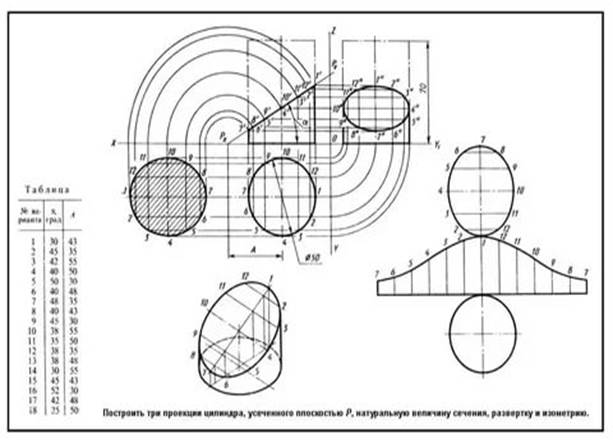
Образец выполнения графической работы №6(2 часть)

Начиная от этого задания делают те, кто выполнил задания на форматах А3 по гр.раб.№5(1и2 часть) и гр.раб.№6(1и2 часть)

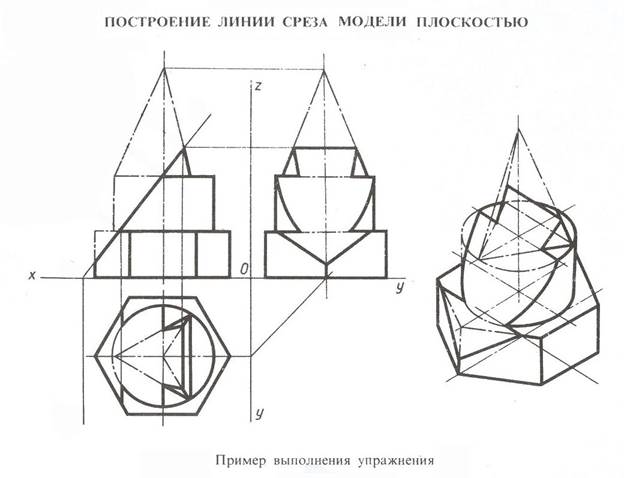
Таблица №1 с 1по 10 вариант

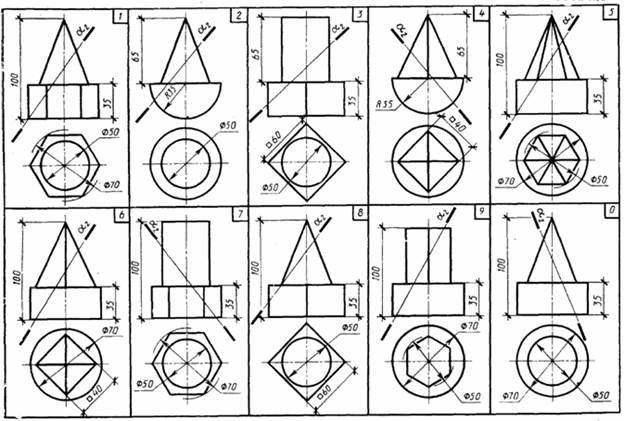
Таблица №2 с 1по 30 вариант

 

Литература:

1. Р.С. Миронова, Б.Г. Миронов. «Инженерная графика»
Москва «Высшая школа» 2016

2. Миронова Р. С., Миронов Б.Г. М 64 Сборник заданий по инженерной графике: Учеб. Пособие. – 2-е изд., испр. – М.: Высш. Шк.; Изд. Центр «Академия», 2000. – 263 с.: ил. ISBN 5-06-00382-5 (Высшая школа) SIBN 5-7695-0615-6 (Изд. Центр «Академия»).

Ресурсы интернета:

• 3. studopedia.ru ›12_140783_v-ozhidanii-malisha.html

4. seniga.ru ›uchmat/55-kompas/185-unit3..(для обучения компьютерной графике)

5. Чертёж конуса https://www.youtube.com/watch?v=SSsuZWf55IA и цилиндра https://www.youtube.com/watch?v=rOy71vfdAlY https://www.youtube.com/watch?v=nheqP8C8hsc