Задание 1.1. Выполнить действия над матрицами.
| Вариант | Задание | Вариант | Задание |
2(А + В)(2 В - А), где

|
(2 А - В)(3 А + В)-2 АВ, где

| ||
3 А - (А +2 В) В, где

|
(А + В) А - В (2 А +3 В), где

| ||
(А - В)2 А +2 В, где

|
А (2 А + В) - В (А - В), где
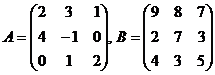
| ||
2(А -0,5 В)+ АВ, где

|
(A – B)(А + В) + 2 А, где

| ||
(А - В) А +3 В, где

| 2 АВ -(А + В)(А - В), где

|
Задание 1.2. Дана система линейных уравнений.
1. Решить систему по формулам Крамера;
2. Решить систему с помощью обратной матрицы.
| Вариант | Задание | Вариант | Задание |

| 
| ||
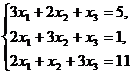
| 
| ||
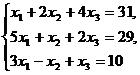
| 
| ||

| 
| ||
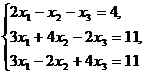
| 
|
Задание 1.3. Решить систему линейных уравнений методом Гаусса.
| Вариант | Задание | Вариант | Задание |
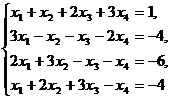
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 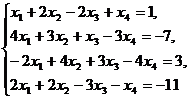
|
Пример выполнения заданий по теме 1
Задание 1.1. Выполнить действия над матрицами: B· (A + 3 B) – A· (A – B), где
А =  ; B =
; B =  .
.
Решение.
1). 3 B = 3 ·  =
=  =
=  .
.
2). A + 3 B =  +
+  =
=  =
= 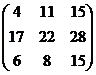 .
.
3). B· (A + 3 B) =  ·
· 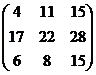 =
=
= 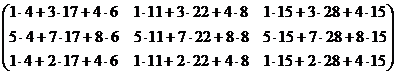 = =
= =  =
=  .
.
4). A – B =  –
–  =
=  =
= 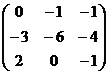 .
.
5). A· (A – B) =  ·
· 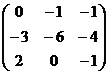 = =
= =  =
=
=  =
=  .
.
6). B· (A + 3 B) – A· (A – B) =  –
–  = =
= =  =
= 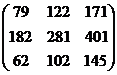 .
.
Ответ: B· (A + 3 B) – A· (A – B) = 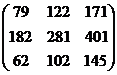
Задание 1.2. Дана система линейных уравнений: 
1. Решить систему по формулам Крамера;
2. Решить систему с помощью обратной матрицы.
Решение.
1. Воспользуемся формулами Крамера: x  =
=  , где j = 1; 2; 3.
, где j = 1; 2; 3.
D = det A, а D j – определитель матрицы, получаемой из матрицы системы заменой столбца j столбцом свободных членов. Тогда
D =  = (5·2·2 + 1·3· (– 1) + (– 1) ·3·4) – (4·2·(–1) + 3·3·5 + 1· (–1) ·2) =
= (5·2·2 + 1·3· (– 1) + (– 1) ·3·4) – (4·2·(–1) + 3·3·5 + 1· (–1) ·2) =
= (20 – 3 – 12) – (–8 + 45 – 2) = 5 – 35 = – 30;
D1 =  = (0·2·2 + 14·3·(– 1) + (–1)·3·16) – (16·2·(–1) + 0·3·3 + 14 ×
= (0·2·2 + 14·3·(– 1) + (–1)·3·16) – (16·2·(–1) + 0·3·3 + 14 ×
× (–1) ·2) = (0 – 42 – 48) – (–32 + 0 – 28) = –90 – (– 60) = – 30;
D2 =  = (5·14·2 + 1·16·(– 1) + 0·3·4) – (4·14·(–1) + 5·16·3 + 1·0·2) =
= (5·14·2 + 1·16·(– 1) + 0·3·4) – (4·14·(–1) + 5·16·3 + 1·0·2) =
= (140 – 16 + 0) – (– 56 + 240 + 0) = 124 – 184 = – 60;
D3 =  = (5·2·16 + 1·3·0 + (–1) ·14·4) – (0· 2·4 + 5·3·14 + 1· (– 1) ·16) =
= (5·2·16 + 1·3·0 + (–1) ·14·4) – (0· 2·4 + 5·3·14 + 1· (– 1) ·16) =
= (160 + 0 – 56) – (0 + 210 – 16) = 104 – 194 = –90.
Тогда x  =
=  1, x
1, x 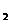 =
=  2, x
2, x  =
=  3.
3.
Ответ: x  = 1; x
= 1; x  = 2; x
= 2; x  = 3.
= 3.
2. Запишем матрицу системы A = 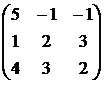 , столбец неизвестных
, столбец неизвестных
X =  , столбец свободных членов B =
, столбец свободных членов B =  . Определитель матрицы A равен
. Определитель матрицы A равен  = – 30
= – 30  0. Тогда решение системы линейных уравнений определяется по формуле X = A
0. Тогда решение системы линейных уравнений определяется по формуле X = A  ·B. Для нахождения A
·B. Для нахождения A  воспользуемся формулой: A
воспользуемся формулой: A  =
=  . Для нахождения A
. Для нахождения A  cоставим для матрицы A транспонированную матрицу A
cоставим для матрицы A транспонированную матрицу A  =
=  и найдем элементы союзной матрицы A
и найдем элементы союзной матрицы A  , как алгебраические дополнения элементов матрицы A
, как алгебраические дополнения элементов матрицы A  .
.
A  = (–1)
= (–1)  .
.
Тогда: A  = (–1)
= (–1)  M
M  =
=  = 2·2 – 3·3 = – 5,
= 2·2 – 3·3 = – 5,
A  = (–1)
= (–1) 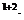 M
M  = –
= –  = –(–1·2 – (–1)·3) = – (– 2 + 3) = – 1,
= –(–1·2 – (–1)·3) = – (– 2 + 3) = – 1,
A  = (–1)
= (–1)  M
M  =
=  = (–1)·3 – (–1)·2 = – 3 + 2 = – 1,
= (–1)·3 – (–1)·2 = – 3 + 2 = – 1,
A  = –
= –  = –(1·2 – 3·4) = – (2 – 12) = – (–10) = 10,
= –(1·2 – 3·4) = – (2 – 12) = – (–10) = 10,
A  =
=  = 5·2 – 4·(–1) = 10 + 4 = 14,
= 5·2 – 4·(–1) = 10 + 4 = 14,
A  = –
= –  = –(5·3 – 1·(–1)) = – (15 + 1) = – 16,
= –(5·3 – 1·(–1)) = – (15 + 1) = – 16,
A  =
=  = 1·3 – 2·4 = 3 – 8 = –5,
= 1·3 – 2·4 = 3 – 8 = –5,
A  = –
= –  = – (5·3 – 4·(–1)) = – (15 + 4) = –19,
= – (5·3 – 4·(–1)) = – (15 + 4) = –19,
A 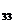 =
=  = 5·2 – 1·(–1) = 10 + 1 = 11.
= 5·2 – 1·(–1) = 10 + 1 = 11.
Тогда A -1 =  =
=  =
=  ;
;
Cделаем проверку:
A×A -1 =  = =
= =  = E.
= E.
Найдем матрицу Х.
Х =  = А-1В =
= А-1В =  ×
× 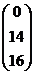 =
=  .
.
Итак, решением системы будет x  = 1; x
= 1; x 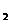 = 2; x
= 2; x  = 3.
= 3.
Ответ: x  = 1; x
= 1; x 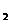 = 2; x
= 2; x  = 3.
= 3.
 Задание 1.3. Решить систему линейных уравнений методом Гаусса:
Задание 1.3. Решить систему линейных уравнений методом Гаусса:
x  + 2 x
+ 2 x 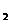 - 3 x
- 3 x  + x
+ x  = - 4,
= - 4,
2 x  + x
+ x 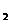 - x
- x  - x
- x  = 1,
= 1,
x  - x
- x 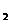 + 2 x
+ 2 x  + 3 x
+ 3 x  = 5,
= 5,
5 x  + 2 x
+ 2 x 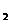 - 4 x
- 4 x  + 2 x
+ 2 x  = - 3.
= - 3.
Решение.
I. Составим расширенную матрицу системы линейных уравнений:

Первую строку матрицы умножим на -2 и прибавим ко второй строке матрицы, также первую строку умножим на -1 и прибавим к третьей строке и умножив первую строку на -5 прибавим ее к четвертой строке. После этого все элементы первого столбца, кроме первого, окажутся равными нулю.

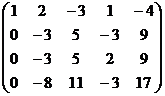 .
.
Четвертую строку умножим на -2 и сложим со второй строкой, умноженной на 5 (таким образом, мы получим на месте элемента a  единицу).
единицу).
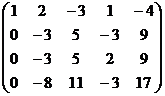
 .
.
Теперь умножим вторую строку сначала на 3 и сложим с третьей, а затем на 8 и сложим с четвертой.

 .
.
Разделим все элементы четвертой строки на 5.

 .
.
Переставим четвертую и третью строки местами.


Умножим третью строку на -2 и сложим с четвертой.


В результате мы получили треугольную основную матрицу системы линейных уравнений. Запишем соответствующую данной расширенной матрице систему линейных уравнений и решим ее.
II. x  + 2 x
+ 2 x 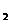 - 3 x
- 3 x  + x
+ x  = - 4 ,
= - 4 ,
 x
x 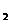 + 3 x
+ 3 x  - 9 x
- 9 x  = 11,
= 11,
7 x  - 15 x
- 15 x  = 21,
= 21,
5 x  = 0.
= 0.
Из последнего уравнения системы находим x  = 0. Подставим x
= 0. Подставим x  = 0 в третье уравнение и найдем x
= 0 в третье уравнение и найдем x  = 3. Подставим x
= 3. Подставим x  = 0 и x
= 0 и x  = 3 во второе уравнение системы, получим: x
= 3 во второе уравнение системы, получим: x 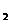 + 3·3 - 9·0 = 11, из которого находим x
+ 3·3 - 9·0 = 11, из которого находим x 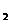 = 2. Подставим x
= 2. Подставим x  = 0, x
= 0, x  = 3, x
= 3, x 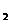 = 2 в первое уравнение системы, получим:
= 2 в первое уравнение системы, получим:
x  + 2·2 - 3·3 + 0 = - 4, из которого получаем: x
+ 2·2 - 3·3 + 0 = - 4, из которого получаем: x  = 1.
= 1.

 Проверка. Подставим найденные значения x
Проверка. Подставим найденные значения x  , x
, x 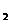 , x
, x  , x
, x  в исходную систему линейных уравнений:
в исходную систему линейных уравнений:
1 + 2·2 – 3·3+ 0 = – 4, – 4 = – 4 – верно,
2·1 + 2 – 3 – 0 = 1, 1 = 1 – верно,
1 – 2 + 2·3 + 3·0 = 5, 5 = 5 – верно,
5·1 + 2·2 – 4·3 + 2·0 = – 3. – 3 = – 3 – верно.
Ответ: x  = 1; x
= 1; x 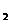 = 2; x
= 2; x  = 3, x
= 3, x  = 0.
= 0.
Тема 2. Аналитическая геометрия