Кинематический анализ и синтез зубчатых механизмов

Краткое содержание: Сложные зубчатые механизмы. Многоступенчатые и планетарные механизмы. Кинематика рядного и ступенчатого зубчатого механизма. Формула Виллиса для дифференциальных механизмов. Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами. Постановка задачи синтеза планетарных механизмов. Условия подбора чисел зубьев. Условия соосности, соседства и сборки. Примеры решения задач по подбору чисел зубьев.

При проектировании зубчатых механизмов многих машин и приборов возникает необходимость обеспечить передачу вращения с большим передаточным отношением или при значительных межосевых расстояниях. В таких случаях применяют многозвенные зубчатые механизмы – либо редукторы, снижающие скорость вращения выходного вала по сравнению со скоростью входного звена, либо мультипликаторы, повышающие ее.

Многозвенные зубчатые механизмы подразделяются на два вида: 1) механизмы с неподвижными осями всех колес (рядовые и ступенчатые зубчатые механизмы); 2) механизмы, в которых оси отдельных колес перемещаются относительно стойки (планетарные и дифференциальные механизмы).

Механизмы с неподвижными осями зубчатых колес имеют число степеней свобод, равное единице, благодаря чему передаточное отношение постоянно.

Общее передаточное отношение многозвенного зубчатого механизма равно произведению передаточных отношений отдельных ступеней:

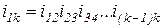
Рядовые зубчатые механизмы представляют собой последовательное соединение нескольких пар зубчатых колес (рис. 14).

Общее передаточное отношение рядового зубчатого механизма постоянно и равно обратному отношению чисел зубьев или радиусов крайних колес:

.

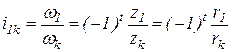Знак передаточного отношения определяется множителем 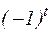, где 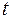- число передач внешнего зацепления. Но передаточное отношение в таких передачах невелико, так как оно ограничено допустимой величино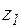й и 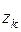, а числа зубьев промежуточных колес не влияют на величину общего передаточного отношения механизма, поэтому их называют паразитными колесами.

Рис. 14

Ступенчатые зубчатые механизмы (рис. 15) представляют собой последовательное соединение блочных (спаренные колеса 1 и 2; 2^” и 3) или одиночных зубчатых колес. В общем случае при j колесах и t внешних зацеплениях полное передаточное отношение ступенчатой передачи

^,

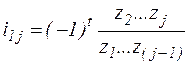т.е. равно отношению произведения чисел зубьев ведомых колес к произведению ведущих колес.

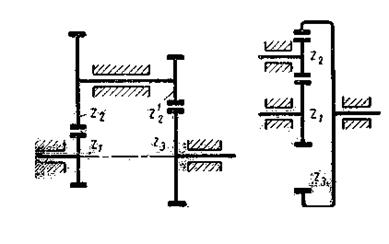
Рис. 15

Зубчатые механизмы с подвижными осями имеют колеса с движущимися геометрическими осями, которые называются саттелитами. На рис. 16 показана схема планетарного механизма: подвижное звено – h, в котором помещены оси саттелитов, называется водилом; вращающееся неподвижной оси колесо – 1, по которому обкатываются саттелиты, называется центральным; неподвижное центральное колесо – 3 называется опорным. Как правило, планетарные механизмы изготовляются соосными, это означает, что оси колес 1, 3 и водила h находятся на одной прямой.

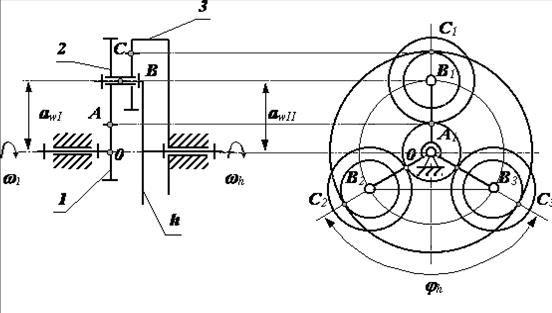
Рис. 16

Обычно у реального механизма имеется несколько симметрично расположенных саттелитов. Их вводят для того, чтобы снизить усилия в зацеплении, разгрузить подшипники центральных колес, улучшить уравновешивание водила. Но при кинематических расчетах учитывается только один саттелит, так как остальные являются пассивными в кинематическом отношении.

Аналитический метод исследования планетарных механизмов основан на способе обращения движения. Всем звеньям механизма сообщается угловая скорость, равная по величине и противоположная по направлению угловой скорости водила 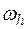. Тогда водило становится неподвижным, и механизм из планетарного обращается в зубчатый механизм, состоящий из нескольких последовательно соединенных пар зубчатых колес (1,2 и 2`3). Передаточные отношения планетарного механизма и обращенного механизма 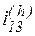связаны условием:

.

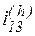
Эта формула справедлива для любой схемы планетарного редуктора при наличии неподвижного центрального колеса. Значит, передаточное отношение от любого саттелита k к водилу при неподвижном опорном колесе j равно единице минус передаточное отношение от этого же колеса к опорному в обращенном механизме:

.

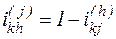Если в планетарном механизме (рис. 16) освободить от закрепления опорное колесо 3 и сообщить ему вращательное движение, то механизм превратится в дифференциал со степенью свободы W = 2 (рис. 17).

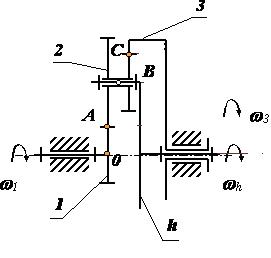
Рис. 17

Для кинематического исследования дифференциальных механизмов используются формула Виллиса, полученная так же на основе метода обращения движения:

,

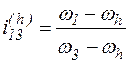Где 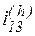- передаточное отношение в обращенном движении ().

Графическое определение передаточного отношения многозвенных механизмов зубчатых можно осуществить методом планов скоростей (треугольников скоростей). Треугольники скоростей можно построить, если известны линейные скорости не менее двух точек звена (по величине и направлению). Используя этот метод и построив треугольники скоростей (рис.18), можно получить наглядное представление о характере изменения скоростей от одного вала к другому, и можно определить графически угловую скорость любого звена (колеса).

Исходные данные: m – модуль зацепления, z_i - числа зубьев колес, .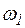

Определить передаточное отношение механизма .

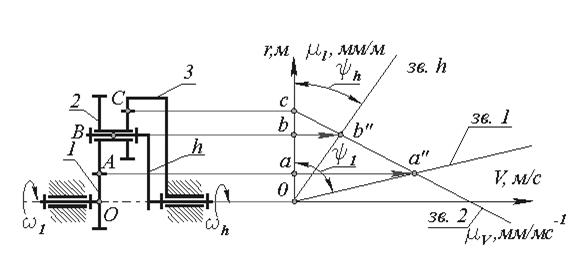
Рис. 18

Решение. Построим кинематическую схему механизма в масштабе 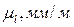, определив радиусы делительных окружностей зубчатых колес

.

Найдем линейную скорость т. А в зацеплении звеньев 1 и 2

.

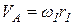В системе координат r0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки а с ординатой r₁ в выбранном произвольном масштабе 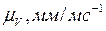отложим отрезок aa”. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси r₁. Эта прямая образует с осью r₁ угол . Так как в точке C скорости звеньев 2 и 3 равны между собой и равны нулю, то, соединяя точку C прямой с точкой a”, получим линию распределения скоростей для звена 2. Так как точка B принадлежит звеньям 2 и h, то ее скорость определяется по лучу сa” для радиуса равного r_B = (r₁+r₂), что в масштабе соответствует отрезку bb”. Соединяя точку b” с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью r угол 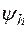. Передаточное отношение планетарного механизма, определенное по данным графическим построениям, можно записать так

.

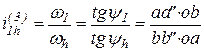Постановка задачи синтеза планетарных механизмов.

При проектировании планетарных механизмов необходимо, кроме требований технического задания (заданного передаточного отношения), выполнять ряд условий связанных с особенностями планетарных и многопоточных механизмов. Задача проектирования и в этом случае может быть разделена на структурный и метрический синтез механизма. При структурном синтезе определяется структурная схема механизма, при метрическом - определяются числа зубьев колес, так как радиусы зубчатых прямо пропорциональны числам зубьев

r_i = m × z_i / 2.

Для типовых механизмов первая задача сводится к выбору схемы из набора типовых схем. При этом руководствуются рекомендуемым для схемы диапазоном передаточных отношений и примерными оценками ее КПД. После выбора схемы механизма необходимо определить сочетание чисел зубьев его колес, которые обеспечат выполнение условий технического задания - для редуктора это передаточное отношение и величина момента сопротивления на выходном валу. Передаточное отношение задает условия выбора относительных размеров зубчатых колес - чисел зубьев колес, крутящий момент задает условия выбора абсолютных размеров - модулей зубчатых зацеплений. Так как для определения модуля необходимо выбрать материал зубчатой пары и вид его термообработки, то на первых этапах проектирования принимают модуль зубчатых колес равным единице, то есть решают задачу кинематического синтеза механизма в относительных величинах.

При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при числе сателлитов и заданном передаточном отношении необходимо подобрать числа зубьев колес, которые обеспечат выполнение ряда условий.