Рассмотрим примеры исследования элементарных функций на уроках математики
1) Функция y = f (x) + b. График этой функции строится путем параллельного переноса графика функции y = f (x) на вектор (0; b) вдоль оси ординат. Обозначим здесь и далее через 
координаты точки, в которую переходит произвольная точка (x; y) координатной плоскости при данном преобразовании. [8]
Пусть f - произвольная функция с областью определения D (f). Выясним, в какую фигуру переходит график этой функции при данном переносе. Получаем, что произвольная точка имеет следующие координаты: (x; f (x) + b), где xєD (f).
Когда сам график сложный в построении перемещать его очень сложно, в таком случае целесообразнее вместо графика переносить оси. Так, для построения графику функции y = f (x) + b, надо переместить ось ОХ на вектор (0; -b).
Пример. Построим график функции: а) y = sin x + 2
В соответствии с правилом переносим график функции y = sin x на вектор (0, 2), то есть вверх по оси OY на 2 единицы (рис 2.7).

Рисунок 2.7. y = sin x + 2
2) Функция строится графически путем растяжения графику функции y = f (x) вдоль оси OY в k раз. Такое преобразование можно задать формулами: 
Для построения точки M ', в которую переходит данная точка M при растяжении, надо построить на прямой АМ, где А - проекция М на ось OХ, точку, ордината которой изменена в k раз относительно ординаты точки M. На рисунке 2.8. показано построение точек, в которые переходят данные при растяжениях с k  и k=-2.
и k=-2.

Рисунок 2.8.Переход точек
Пример: Построим графики функций  и
и  .
.
Построение осуществляется в первом случае из графика функции y = x2 (рис. 2.9), а в другом случае - с графика y=cosx (рис.2.10)

Рисунок 2.9. y = x2
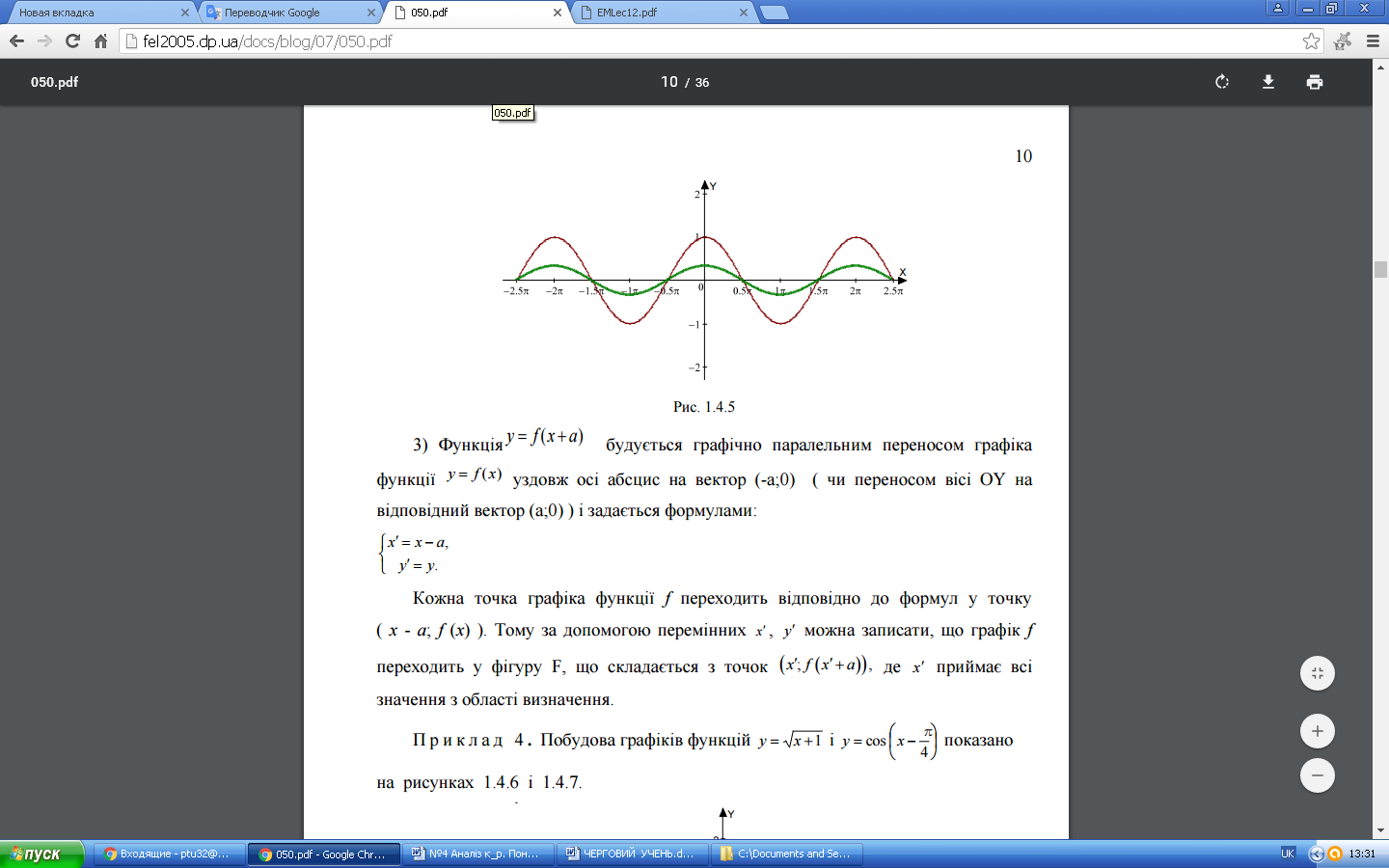
Рисунок 2.10 y=cosx
Рассматривая графики функций, содержащих модули, надо помнить как общие свойства модуля, так и правила отражения на координатной прямой.
Существуют функции, которые содержат переменную не только под знаком модуля. графики такого типа строят, рассматривая функцию на интервалах, где функция имеет постоянный знак (Методом интервалов). [2]
Алгоритм и особенности схематической построения графиков дробно-рациональной функции:
1. Определим область определения функции (D (y)), нули знаменателя будут точками, через которые проходят вертикальные асимптоты или точками разрыва графика, если такой же корень имеет числитель.
2. Найдем нули числителя, они будут нулями заданной функции.
3. Определим промежутки знакопостоянства и поведение функции на этих промежутках и при приближении аргумента к точкам разрыва и к ± ∞.
4. Учитывая полученные результаты, схематично строим график функции.
Заключение
В данной научно исследовательской работе рассмотрены способы схематической построенияграфиков сложных функций с помощью преобразования плоскости и анализасвойств составляющих функции.
Выполнив построение графиков сложных функций различных типов (от графиков смодулем, графиков дробно-рациональных функций), я пришел к выводу, что знаниязакономерностей между зависимыми функциями позволяют получить наглядную картину,определить поведение функции и схематично построить ее график. Замечено, чтолюбая сложная функция является функцией одной или нескольких элементарных функций.
Поэтому пользуясь элементарными методами анализа функции и графическихпреобразований на координатной плоскости можно схематично строить графики различныхтипов сложных функций. [1]
При графическом построении функций главную роль должен был качественный анализ функции. Поэтому наоснове выполненных графических построений был определен следующий алгоритмисследование функции и построения графика:
1. Определение ОПФ функции и точек ее разрыва на координатной прямой.
2. Определение нулей функции (точек пересечения оси ОХ)
3. Определение четности и периодичности функции.
4. Определение промежутков знакопостоянства (используя нули и разрывыфункции).
5. Нахождение вертикальных, горизонтальных и наклонных асимптот.
6. Исследование поведения функции при приближении к точкам разрыва и при 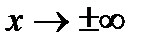 .
.
7. По данным анализа построить график функции.
Исследование функции нужно выполнять с одновременным схематичными очерками накоординатной плоскости (построением асимптот, точек пересечения осей, точек-экстремумов; обозначением промежутков возрастания и убывания, знакопостоянства). Далее,учтя все свойства функции, ОПФ и ОЗФ, проанализировав каждыйпромежуток, можно схематично строить график. Для улучшения точности графику,можно подкорректировать его на сомнительных участках, используя метод построенияграфике по точкам.
Для построения графика не обязательно использовать полный анализ функции,можно рассматривать только те свойства, которые имеют смысл для данной функции. Однакоможно прекращать анализ, не получив сформирован график.
Поэтому при построении графиков сложных функций были сформированы общие принципыанализа и построения графиков элементарными методами, что позволило более глубокопроникнуть в разнообразие графических изображений функций и их свойств.
При выполнении работы были достигнуты следующие результаты:
1) Выполняяпостроение различных графиков функций, были рассмотрены общие принципы исследованияфункции и построения их графиков;
2) было рассмотрено комплексное применение различныхметодов построения графиков функций;
3) Были рассмотрены сложные функции и выполненыпостроения соответствующих графиков.
4) Выполняя работу, были получены болееглубокие знания по анализу и графического построения функций.
Данная курсовая работа может быть использована учащимися, для получения дополнительныхзнаний относительно построения графиков функций и учителями математики при проведениифакультативных занятий.
Список использованной литературы
1. Амелькин В. Задачи з параметром: збірник задач / В. Амелькин — Минск, 1994. – 88 с.: ил..
2. Графики дробно-рациональной функции [Електронний курс]: arm-math.rkc- 74.ru – 1000кб – Доступ до режиму: arm-math.rkc-74.ru/DswMedia/grafikidrobnoracional-noyfunkcii.doc. 7. Графики и их функции [Електронний курс]: https://www.omsu.ru – 2300 кб – Доступ до режиму: https://www.omsu.ru/file.php?id=611
3. Лурьве М. В., Александров Б. И. Задачи на составление уравнений: Учеб. рук- во. — 3-е изд., перераб. / М. В. Лурьве, Б. И. Александров. — М.: Наука, 1990. — 96 с.
4. Махмутов М. Й. Проблемноє обучение. -М.: Педагогика, 1975. – 240 с.
5. Мордкович А. Г. Набольшее и наименьше значения величин. / А. Г. Мордкович. — М.: Школа-Пресс, 1995. — 144 с.
6. «Сложение графиков функций» [Електронний курс]: www.arm-math.rkc-74.ru – 808 кб – Доступ до режиму: www.arm-math.rkc-74.ru/DswMedia/grafikifunkciy.doc
7. Построение графиков сложных функций [Електронний курс]: https://festival.1september.ru – 352 кб – Доступ до режиму: https://festival.1september.ru/files/articles/52/5286/528629/pril.doc.
8. Шахно Г. У. «Сборник задач по элементарной математике повышенной трудности» / Г. У. Шахно. – Мінськ: «Высшая школа» 1965 р. – 523 с.: ил.
9. Шилов Г. Е. «Как строить графики», збірник лекцій / Г. Е. Шилов. – Випуск 30 – Москва: ФИЗМАТГИЗ 1959. – 28 с.: ил.