Совокупность насоса и переливного клапана называется насосной установкой (НУ). Зависимости давления от расхода называются характеристиками: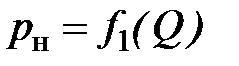 
– насоса, 
– клапана, 
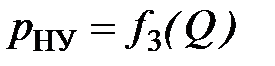– насосной установки. Вначале строятся характеристики насоса и переливного клапана, а затем всей насосной установки.
Характеристики насоса и клапана близки к линейным, поэтому их можно построить по двум точкам.
Для насоса первая точка А на рисунке 2.3 соответствует нулевому значению давления 
при теоретической подаче насоса, определяемой по формуле
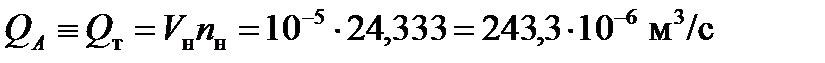(243,3 см3/с),
вторая точка 
определяется по объёмному кпд насоса 
, заданному по условию задачи при давлении 
,
.
Для клапана характеристика также линейна и имеет вид
. (2.1)
В качестве первой точки К удобно взять точку при нулевом значении расхода (
).
Тогда в соответствии с (1.1) 
. Вторая точка 
на рисунке 2.3 определяется по формуле (1.1) при произвольном расходе через клапан, например, 
:
.
По найденным координатам строим характеристики насоса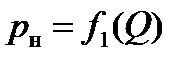 
(линия 
) и переливного клапана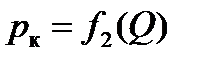 
(линия 
) на рисунке 2.3. Эти линии можно представить в виде зависимостей давления от расхода, что удобно при использовании прикладной программы Mathcad для решения данной курсовой работы).
Уравнения линий получают из условия подобия треугольников. В качестве примера на рисунке 2.3 рассматривается подобие треугольников 
и 
для линии 
– характеристики насоса:
или 
.
Откуда
. (2.2)
Аналогичным образом выводится уравнение линии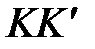 
– характеристики клапана
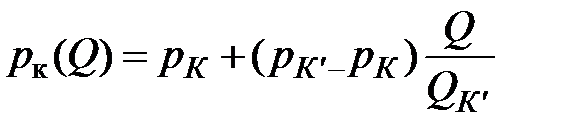. (2.3)
Для получения характеристики насосной установки, или суммарной характеристики насоса и переливного клапана проводим графическое сложение их характеристик. Поскольку переливной клапан постоянно участвует в работе насосной установки, то характеристика насосной установки будет представлять собой суммарную характеристику, получаемую в соответствии с условием
. (2.4)
Поскольку исходные характеристики – прямые линии, то и суммарная характеристика будет состоять из отрезков прямых линий (ломаная линия 
на рисунке 2.3). Точка 
определится на пересечении горизонтали для минимального давления в клапане (точка К) с линией 
, так как в точке К 
и в соответствии с (2.4) 
. Точка С определяется на пересечении с осью давления горизонтали, проходящей через точку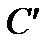 
– точку пересечения характеристик насоса и клапана (при этом давлении суммарный расход равен нулю 
).
Значения давления и расхода в точке 
, можно определить также аналитически путём совместного решения уравнений (2.2) и (2.3) для линий 
и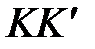 
. В точке 
давления насоса и клапана одинаковы 
Приравнивая правые части уравнений (2.2) и (2.3) и выражая в явном виде расход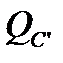 
от известных величин, находим 
.
Рассматривая подобные треугольники для прямой линии 
, входящей в состав характеристики насосной установки, можно получить её уравнение в виде
. (2.5)
Для оценки возможного режима течения жидкости в трубопроводе определяем число Re по максимально возможному расходу в нём 
,
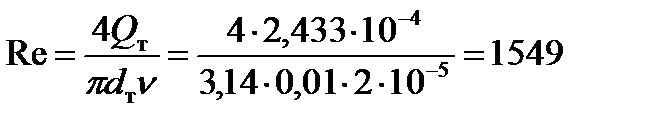что меньше критического значения числа Рейнольдса 
. Следовательно, в трубопроводе возможен только ламинарный режим течения жидкости.