ГОСТом предусмотрен единый блок для обозначения различных циклов (Рисунок 11). В блоке, соответствующем началу цикла указывается имя цикла (Как правило, это одна буква латинского алфавита) и начальное значение переменной цикла. В зависимости от оператора цикла, условие окончания записывается либо в блоке, соответствующем началу цикла (для операторов FOR…DO и WHILE…DO), либо в блоке, соответствующем концу цикла (для оператора REPEAT…UNTIL). Аналогично записывается и шаг изменения переменной цикла.
Примеры использования различных операторов цикла
Пример 15.
Вычислить сумму:
.
Значения величин A, B, m, n ввести с клавиатуры. Алгоритм решения данной задачи описывается с помощью следующей структурограммы:
| Ввод с клавиатуры A, B, m, n; S:=0; | |
| Для I от M до N c шагом +1 делать: | |
| S=S+I2/(N+I); | |
| Вывод на экран значение (A+B*S). |
PROGRAM PR15;
VAR
А, X, S: REAL;
I, М, N: INTEGER;
BEGIN
WRITELN('BBEДИTE A, B, M и N');
READLN(A, B, M, N);
S:=0;
FOR I:=M TO N
DO S:=S + I*I/(N + I);
WRITELN('S = ', A+B*S:6:4)
END.
Большое значение имеет стиль написания программы. Для облегчения просмотра текста рекомендуется по возможности придерживаться следующих правил при составлении текста вашей программы.
• Оператор END начинать с той же позиции, что и соответствующий ему оператор BEGIN. Это удобно в тех случаях, когда в программе используются вложенные составные операторы.
• Оператор DO писать под соответствующим оператором FOR.
• Операторы THEN и ELSE писать под соответствующим оператором IF.
Пример 16.
Найти сумму S всех целых чисел, кратных 3 на отрезке [ М, N ].
Эта задача похожа на предыдущую. Отличие состоит в том, что, просматривая все числа из интервала [ М, N ], мы должны проверить, делится ли число I без остатка на 3 прежде, чем его суммировать к S. Для проверки деления используется операция mod – деление с остатком целых чисел. Таким образом, условие деления числа I на 3 без остатка будет иметь вид: I mod 3 = 0.
|
|
Алгоритм решения этой задачи отличен от предыдущего наличием условия в теле
арифметического цикла и описан с помощью приведенной ниже структурограммы.
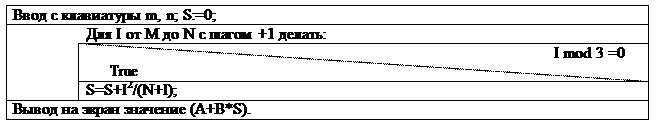PROGRAM PR16;
VAR X, S: REAL;
I, M, N: INTEGER;
BEGIN
WRITELN('BBEДИTE M И N');
READLN(M, N);
S:=0;
FOR I:=M TO N
DO IF I MOD 3 = 0
THEN S:= S + I;
WRITELN('S=', S:6:4)
END.
Табулирование функции
Задача табулирования функции предполагает получение таблицы значений функции при изменении аргумента с фиксированным шагом. В качестве исходной информации должны быть заданы: Х0, Хn – начало и конец промежутка табулирования, при этом (Х0< Хn); n – число шагов разбиения промежутка [ Х0, Xn ]; F(X) – описание табулируемой функции.
При составлении алгоритма предполагается, что X – текущее значение аргумента; h – шаг изменения аргумента (иногда его называют шагом табуляции функции); i – текущий номер точки, в которой вычисляются функция (i = 0.. n).
Количество интервалов n, шаг табуляции h и величины Х0, Хn связаны между собой формулой:
Интерпретация переменных (т. е. их обозначение в математической постановке задачи, смысл и тип, обозначения в блоксхеме и программе) приведена в таблице имен.
Таблица имен
| Математ. величина | Обозначение в программе | Содержательный смысл | Тип переменной |
| n | N | Число интервалов разбиения [Хо, Хn] | integer |
| Х0 | Х0 | Начало промежутка | real |
| Хn | XN | Конец промежутка | real |
| X | X | Текущее значение аргумента | real |
| F(X) | Y | Текущее значение функции | real |
| h | Н | Шаг табулирования | real |
|
|
Пример 17.
Табулировать функцию F(X) в N равноотстоящих точках, заданную на промежутке [ Х0, Xn ], где
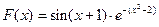
PROGRAM PR17;
VAR
I, N: INTEGER;
X, Y: REAL;
H, X0, XN: REAL;
BEGIN
WRITELN('ВВЕДИТЕ X0, XN, N');
READLN(X0, XN, N);
H:= (XN - X0)/N;
FOR I:=0 TO N
DO BEGIN
Y:= SIN(X+1)*EXP(2-X*X);
X:= X0 + I * H;
WRITELN (X:4:1,",Y:9:6)
END
END.
Теперь запишем решение этой же задачи, но с использованием цикла While...DO.
PROGRAM PR17_while;
VAR
N: INTEGER;
X, Y: REAL;
H, X0, XN: REAL;
BEGIN
WRITELN('ВВЕДИТЕ X0, XN, N');
READLN(X0, XN, N);
H:= (XN - X0)/N;
X:=X0;
WHILE X<=XN
DO BEGIN
Y:= SIN(X+1)*EXP(2-X*X);
X:= X + H;
WRITELN (X:4:1,",Y:9:6)
END
END.
Арифметический цикл с рекуррентной зависимостью
Многие циклические вычислительные процессы используют рекуррентные зависимости при решении различных математических задач. В общем виде формулу для рекуррентных вычислений можно представить так:
В этой рекуррентной формуле для вычисления i -го члена последовательности Yi, где i > k, используются k предыдущих членов последовательности 
. Для вычислений по этой формуле нужно задать k первых членов последовательности – 
.
Использование рекуррентных формул, как правило, сокращает текст программы и время ее выполнения на компьютере. Однако в большинстве случаев рекуррентную формулу нужно написать программисту, что в ряде случаев вызывает определенные трудности.
Пример 18.
Вычислить значение tgx:
Знаменатель формулы для вычисления tgX представляет собой цепную дробь. Для вычисления такого знаменателя в цикле удобно использовать рекуррентную зависимость с памятью в один член последовательности Аi= F(Ai-1). Для вывода рекуррентной формулы следует использовать таблицу 18.
|
|
Таблица 18
| Номер 1 | Член последовательности | Величина |
| A0 | ||
| A1 | 
| |
| A2 | 
| |
| A3 | 
| |
| A4 | 
| |
| A5 | 
|
Из таблицы 23 видно, что рекуррентная формула принимает вид:
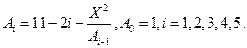
PROGRAM PR18;
VAR
X, A: REAL;
I: INTEGER;
BEGIN
WRITELN('BBEДИTE X');
READLN(X);
A:= 1;
FOR I:= 1 TO 5
DO A:= 11 - 2 * I - X * X/A;
WRITELN('tgX = ', X/A:8:5)
END.
Пример 19.
Пользуясь рекуррентной формулой, для заданного N вычислить 
, известны Y0, Y1, Y2, a Yi (i≥3) вычисляется по формуле:
.
Таблица имен
| Математ. величина | Обозначение в программе | Содержательный смысл | Тип переменной |
| N | N | Номер последнего члена последовательности SN | integer |
| Y0, Yi-3 | Y3 | Член последовательности с номером i-3 | real |
| Y1, Yi-2 | Y2 | Член последовательности с номером i-2 | real |
| Y2, Yi-1 | YI | Член последовательности с номером i-1 | real |
| Yi | Y | Член последовательности с номером i | real |
| SN | S | Искомая сумма | real |
Первым шагом в работе алгоритма является ввод данных Y0, Y1, Y2, N. При вводе трех первых значений последовательности нужно использовать рабочие ячейки Y3, Y2 и Y1 соответственно. На втором шаге требуется проанализировать значение N. Если N < 3, то рекуррентная формула для подсчета S суммы первых N членов не потребуется. Для определения S при условии N < 3 в алгоритме предусмотрен переключатель (оператор CASE), имеющий три ветви: N = 0, N = 1 и «В противном случае», куда попадает и случай N = 2. Для каждой ветви подсчитывается соответствующая сумма S. Третий шаг выполняется только в том случае, если N > 2. На этом шаге для I от 3 до N по рекуррентной формуле вычисляются Y, и подсчитывается их сумма S. Найденное значение S на последнем четвертом шаге выводится на экран.
PROGRAM PR19;
VAR
Y3, Y2, Yl, Y, S: REAL;
I, N: INTEGER;
BEGIN
WRITELN('ВВЕДИТЕ Y0, Yl, Y2, N');
READLN(Y3, Y2, Yl, N);
CASE N OF
0: S:= Y3;
1: S:= Y3 +Y2
ELSE S:= Y3 + Y2 + Y1
END; {CASE}
IF N > 2
THEN FOR I:= 3 TO N
DO BEGIN
Y:= LN(ABS(Y1*Y1 + Y3 + 1));
S:= S + Y;
Y3:= Y2;
Y2:= Y1;
Y1:= Y
END;
WRITELN('S=', S:10:8)
END.
Вложенный арифметический цикл
Под вложенным арифметическим циклом понимают такую алгоритмическую структуру, при которой в тело одного цикла с параметром включен другой цикл со своим параметром. Другими словами составная инструкция:
FOR I:=...
DO FOR J:=...
DO...
является признаком вложенного арифметического цикла.
Пример 20.
Вычислить 
Для решения этой задачи необходима дополнительная переменная, как иногда говорят, рабочая ячейка R для накопления в процессе вычисления S вложенной суммы:
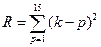
PROGRAM PR20;
VAR
R, S: REAL;
К, P: INTEGER;
BEGIN
S:=0;
FOR K:=1 TO 10
DO BEGIN
R:=0;
FOR P:=1 T0 15
DO R:= R + SQR(K - P);
S:=S + K*K*K*R
END;
WRITELN('S=', S:10:8)
END.
Количество уровней вложения арифметических циклов может быть более трех десятков. В следующем примере используется алгоритмическая конструкция, имеющая шесть уровней вложения арифметических циклов.
Пример 21.
Используя вложенный цикл, определить число счастливых билетов S, номера которых меняются от 000001 до 999999.
В основе алгоритма решения этой задачи лежит принцип десятичного счетчика, имеющего шесть разрядов. Роль разрядов играют индексы в следующем порядке I, J, К, L, М, N. Счастливым называется такой номер, у которого три левых разряда в сумме равны сумме трех правых разрядов, то есть I+J + K = L + M + N.
PROGRAM PR24;
VAR
S: REAL;
I, N, J, K, L, M: INTEGER;
BEGIN
S:=-l;
FOR I:= 0 TO 9
DO FOR J:=0 TO 9
DO FOR K:=0 TO 9
DO FOR L:=0 TO 9
DO FOR M:=0 TO 9
DO FOR N:=0 TO 9
DO
IF I+J + K = L+M + N
THEN S:=S+ 1;
WRITELN('Число счастливых билетов = ', S:6:0)
END.
В связи с тем, что номер 000000 в катушке билетов отсутствует, то этот номер нужно вычесть из найденного числа. Это можно сделать разными способами. В предложенном алгоритме это реализовано так S:= -1. Это решение логично. При исходном состоянии счетчика: I = 0, J = 0, К = 0, L = 0, М = 0, N = 0, условие I + J + K = L +М + N принимает значение TRUE, и S становится равным нулю S = -1 + 1 = 0. Таким образом, все переменные приняли исходное значение для дальнейших расчетов.
Основным достоинством вложенного цикла является возможность в выражениях (в заголовке цикла или его теле) использовать параметры внешних циклов. Например, в описанном выше примере, в теле цикла с параметром N используются также текущие значения параметров I, J, К, L, М внешних циклов по отношению к этому циклу. К параметрам внутренних циклов из внешнего цикла не должно быть обращений. Транслятор с Паскаля такие обращения не проверяет, но для внешних циклов значения параметров внутренних циклов не определено. Допускается выход из тела цикла FOR... DO... любого уровня вложения на любой предыдущий
уровень до полного завершения цикла с помощью оператора GOTO, но не рекомендуется это делать. При выходе из цикла (досрочном или нормальном) значение параметра цикла становится неопределенным. Можно непосредственно из цикла завершить работу программы. Для этой цели используют оператор HALT [(Код)], где код — это необязательный параметр, представляющий собой целое число типа WORD, которое является кодом возврата вашего ЕХЕ модуля.
Пример 22.
Вычислить 
. Вычисления остановить при выполнении условия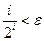 
.
Для решения этой задачи удобно использовать оператор цикла с предусловием
WHILE...DO.
PROGRAM PR22;
VAR
У, Е: REAL;
I: INTEGER;
BEGIN
WRITELN('ВВЕДИТЕ E');
READLN(E);
I:= 1; Y:=0.5;
WHILE I * EXP(-I * LN(2)) > E
DO BEGIN
Y:=Y + I*EXP(-I*LN(2));
I:= I+ 1;
END;
WRITELN('Y =', Y:12:8)
END.
Пример 23.
Вычислить с точностью ε квадратный корень из величины 
.
Вычисление проводить по рекуррентной формуле:
выбрав в качестве начального приближения величину
При решении подобных задач условие остановки вычислительного процесса
формулируется следующим образом: | Yi — Yi-1 |<ε.
| Математ. величина | Обозначение в программе | Содержательный смысл | Тип переменной |
| i | I | Номер итерации | integer |
| Yi-1 | Y1 | Член послед. У с номером i-1 | real |
| Yi | У | Член последовательности У с номером i | real |
| X | X | Величина X, квадратный корень которой мы ищем | real |
| ε | Е | Требуемая точность расчетов | real |
Вводим с клавиатуры величины X и Е. Далее вычисляем первое приближение Y. Если X<1, то Y принимается равным X, в противном случае за Y принимается величина Х/2. Далее на основании Y нужно найти следующее приближение. Поэтому вычисленное значение записывается в ячейку с именем Y1 и с этого момента времени считается предыдущим значением. Текущее значение Y рассчитывается по рекуррентной формуле на основании Y1 и X. Этот циклический процесс повторяется до тех пор, пока не выполнится условие | Y — Y1 | < Е. После чего Y считается равным значению корня из X с точностью Е и выводится на экран монитора.
PROGRAM PR23;
VAR
X, Y, YI, E: REAL;
BEGIN
WRITELN('BBEДИTE X, E');
READLN(X, E);
Y:= X;
IF X>= 1 THEN Y:= Y/2;
REPEAT
Y1:=Y;
Y:= (Y1 +X/Y1)/2
UNTIL ABS(Y-Y1)<E;
WRITELN(Y =', Y:12:8)
END.