Нечеткое множество, или фаззи-множество (в англ. - fuzzy set) А, - совокупность всех пар вида (х, mА(х)), которая образована из значений базовой переменной х ÎХ и из функций принадлежности mА(х), устанавливающих связь между этими значениями и числами в интервале [0, 1], т.е.
| (2) |
Для приведенного выше примера с тепловым режимом в помещении (см. рис. 2, г) существуют пять фаззи-множеств, характеризуемых функциями m l (х): mж(х) – «жарко», mт(х) – «тепло» и т.д.
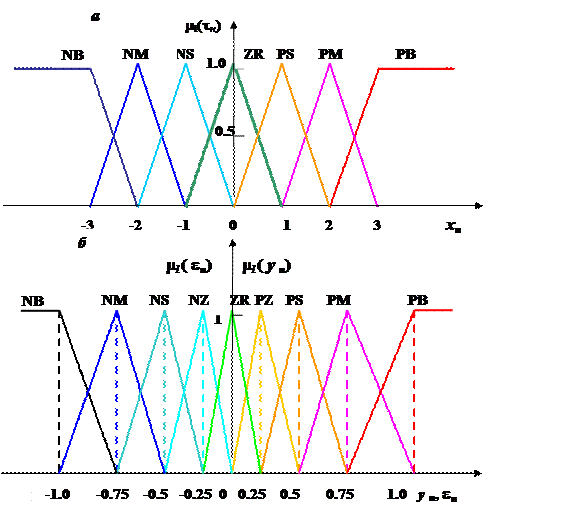
| Рис. 3. Унифицированные системы функции принадлежности для нормированных значений переменной состояния (а), ошибки регулирования (б, тонкие линии) и управляющего воздействия (б, вертикальные линии) |
Множество А состоит из элементов, каждый из которых характеризуется парой значений (х i, m i (х)). Такую элементарную составляющую нечеткого множества называют синглтоном (в англ. - singleton). Пример синглтона – дискретные значения функций ml(у) на рис. 3, б.
Любое нечеткое множество А можно рассматривать как объединение синглтонов, которое в общем случае - для бесконечно большого количества элементов - обозначают так:
 .
| (3) |
Если фаззи-множество А состоит из конечного числа элементов, то вместо условного обозначения в виде интеграла (3) используют сумму
 .
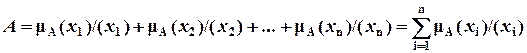| (4) |
Здесь, как и в выражении (3), знак дроби не означает деление, а суммирование (или интегрирование) соответствует принятой в теории множеств операции объединения, т.е.
 .
| (5) |
Процедура введения терм-множеств А, их функций принадлежности mА(х) и установления конкретного значения mА(х *), соответствующего измеренному значению х *, называется фаззификацией.
Для фаззи-множеств применимы все свойства и oперации, используемые для обычных множеств. Так, фаззи-множества А и В равны друг другу, если равны их ФП mА и mВ, т. е.
| А = В, если mА (х) = mB(х), х Î Х. | (6) |
Фаззи-множество А включает в себя фаззи-множество В, т. е.
| В Í А, если mB(х) £ mА(х), х Î Х. | (7) |
Фаззи-объединением двух нечетких множеств А и В, заданных на общем базовом множестве Х, называют наименьшее нечеткое множество С, которое содержит одновременно как А, так и В и имеет вид
 С:= А È В  {(х, mАÈВ(х))½ х Î Х },
| (8) |
Где
mС(х) = mАÈВ(х) = max{mА(х), mВ(х)} 
| (9) |
Символы:= и означают «равно по определению». Фаззи- пересечением двух нечетких множеств А и В, заданных на общем базовом множестве Х называют наибольшее нечеткое множество С, которое содержится одновременно и в А и в В и имеет вид
| С:= А Ç В {(х, mАÇВ(х))½ х Î Х },
| (10) |
Где
| mС(х)= mАÇВ(х) = min{mА(х), mВ(х)} | (11) |
Фаззи-дополнением нечеткого множества А, заданного на базовом множестве Х, называют нечеткое множество вида
| ØА {(х, mØА(х)},
| (12) |
Где
| mØА(х) = 1- mА(х). | (13) |
Понятия объединения и пересечения, введенные для случая двух исходных множеств А и В, могут быть распространены и на случай нескольких исходных множеств.
На рис. 4 показано ФП производных фаззи-множеств (8), (10), (12) из ФП mА, mВ, mс треугольной формы, характеризующих три исходных множества А, В и С на интервале [-2,+2].
 |
| Рис. 4. Основные операции над нечеткими множествами |
Основные понятия фаззи-логики
При построении нечетких алгоритмов управления используются различные высказывания - повествовательные предложения естественного или формализованного языка, которые могут быть истинными или ложными. Фаззи-логика изучает логические операции над высказываниями, в которых фигурируют лингвистические переменные и нечеткие множества. Причем, логические операции в фаззи-логике, как и в обычной алгебре логики, служат для получения из нескольких простых, исходных, высказываний одного, более сложного высказывания. Но если в алгебре логики (булевой алгебре) истинность или ложность того или иного высказывания принято обозначать числами 1 (истинность) и 0 (ложность), то в фаззи-логике каждое высказывание (исходное или образованное с помощью логической операции) характеризуется истинностными значениями во всем интервале [0,1].
В табл. 1 приведены истинностные значения 0 или 1, которые характеризуют исходные высказывания А и В и высказывания, образованные с помощью известных логических операций алгебры: отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции. Поясним, что используемая в дальнейшем операция импликации соответствует высказыванию «если А, то В ». При этом высказывание А называется посылкой высказывания А Þ В, а В - его заключением.
Операции алгебры логики (см. табл.1) применимы и к нечетким высказываниям, используемым в фаззи-логике, ecли каждое высказывание, например А, характеризовать функцией истинности (ФИ)- m(А), аналогичной в определенном смысле функции принадлежности.
Таблица 1