| Входные переменные регулятора | Управляющее напряжение U, В | |||||||||
| NB | NM | NS | NZ | ZR | PZ | PS | PM | PB | ||
| Отклонение положения e1, м | NB | ZR | NZ | NS | NM | NB | NB | NB | NB | NB |
| NM | PZ | ZR | NZ | NS | NM | NB | NB | NB | NB | |
| NS | PS | PZ | ZR | NZ | NS | NM | NB | NB | NB | |
| NZ | PM | PS | PZ | ZR | NZ | NS | NM | NB | NB | |
| ZR | PB | PM | PS | PZ | ZR | NZ | NS | NM | NB | |
| PZ | PB | PB | PM | PS | PZ | ZR | NZ | NS | NM | |
| PS | PB | PB | PB | PM | PS | PZ | ZR | NZ | NS | |
| PM | PB | PB | PB | PB | PM | PS | PZ | ZR | NZ | |
| PB | PB | PB | PB | PB | PB | PM | PS | PZ | ZR |
При составлении подобных таблиц, т. е. при лингвистическом синтезе регулятора, предпочтительно, чтобы лингвистические значения управляющею воздействия, располагаемые в соседних по вертикали и горизонтали клетках, соответствовали их “естественному” порядку в принятом терм-множестве (см. рис. 3). Тогда переходные процессы, возникающие в системе при переключении управляющего воздействия с одною значения на другое, будут наиболее плавными. Из этих же соображений стремятся ФП для входных переменных регулятора выбирать так, чтобы они перекрывались, а сумма ординат двух соседних ФП при определенном х н была равна единице.
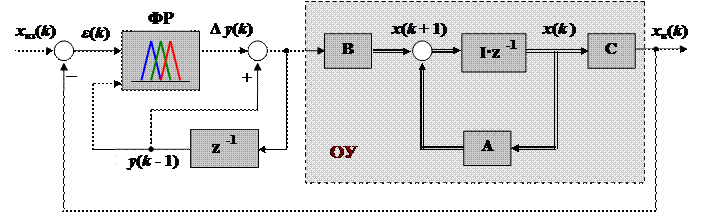 |
| Рис. 14. Структура системы фаззи-регулирования положения тележки |
На основе рассмотренной простейшей системы фаззи-регулирования с одной выходной переменной (перемещение тележки) могут быть синтезированы и более сложные системы - с двумя выходными координатами (перемещение тележки и угол отклонения груза). Причем, эти системы могут быть построены как по принципу последовательного (подчиненного) регулирования, так и с двумя параллельными контурами.
«Пропорционально–интегральный» фаззи-регулятор. Широко используемый в промышленной автоматике линейный непрерывный ПИ- регулятор

| (40) |
можно заменить достаточно близким но стратегии и логике управления фаззи-регулятором, если в качестве его выходной переменной рассматривать приращение управляющего воздействия D у. Действительно, закон регулирования (40) можно представить в следующей дифференциальной форме:
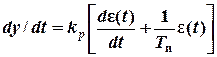
| (41) |
Или в разностной форме
| D y (k) = y (k) – y (k - 1) = k p [ De(k) + (Dt/ T и) e(k)]. | (42) |
Таким образом, для входных переменных e(k) и De(k) и выходной D y (k) может быть синтезирован фаззи-регулятор, реализующий нелинейный закон
| D y (k) = F [e(k), De(k)] | (43) |
и эквивалентный в определённом смысле ПИ-регулятору (40). Лингвистические правила такого ПИ-подобного фаззи-регулятора приведены в табл. 3.
Таблица 3
Лингвистические правила ПИ-подобного фаззи-регулятора
| D e | e | ||||||
| NB | NM | NS | ZR | PS | PM | PB | |
| NB | NB | NB | NB | NB | NM | NS | ZR |
| NM | NB | NB | NB | NM | NS | ZR | PS |
| NS | NB | NB | NM | NS | ZR | PS | PM |
| ZR | NB | NM | NS | ZR | PS | PM | PB |
| PS | NM | NS | ZR | PS | PM | PB | PB |
| PM | NS | ZR | PS | PM | PB | PB | PB |
| PB | ZR | PS | PM | PB | PB | PB | PB |