Лекция 2
Основные законы МСС
- Законы сохранения, 2-й закон термодинамики, уравнения Максвелла
- Определяющие соотношения: закон Фика, реологические соотношения (т.е. соотношения между деформацией и напряжением).
Тензоры напряжений и деформаций
В двумерных и трехмерных задачах деформации и напряжения в сплошной среде описываются тензорами.
Тензор напряжений sij - сила, действующая в направлении j на единичную площадку, перпендикулярную оси i.
Тензор напряжений – симметричный.
 =
= 
Пусть ui является проекцией на ось i перемещения материальной точки с исходным координатным вектором x:
ui =x’i -xi.
Тензор деформаций определяется следующим образом:
uij = ½ (∂ui/∂xj + ∂uj/∂xi + ∂uk/∂xi ∂uk/∂xj)
Расстояние между бесконечно близкими точками dl изменяется:
dl'2 = dl2 + 2uikdxidxk
Тензор деформаций uij является симметричным: uij = uji.
Значения его компонент зависят от системы отсчета. Но есть комбинации компонент – инварианты тензора, которые не зависят от системы отсчета.
Первый инвариант тензора деформации I1 = относительное изменение объема dV/V.
I1 = ∑ uii
Здесь, как обычно при обращении с тензорами, предполагается суммирование по повторяющемуся индексу.
Реологические определяющие соотношения – это соотношения между компонентами uij и их производными и sij и их производными.
Для многих сред в реологических соотношениях присутствует
тензор скоростей деформаций
eij = ∂uij/∂t
Классификация сплошных сред
жидкости sij = - Pii gij + τij
Здесь gij – метрический тензор (единичный тензор для прямоугольной декартовой системы координат), Pii - давление, τij - тензор сдвиговых напряжений.
Ньютоновская жидкость τij = 2η eij
η – коэффициент динамической вязкости
коэффициент кинематической вязкости  , где
, где  - плотность жидкости.
- плотность жидкости.
Рассмотрим одномерное течение Куэтта - в плоскости  происходит течение, при котором скорости частиц жидкости направлены вдоль оси
происходит течение, при котором скорости частиц жидкости направлены вдоль оси  и пропорциональны координате
и пропорциональны координате 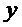 .
.

Деформация является деформацией чистого сдвига. Здесь γ – угол сдвига, dγ/dt – скорость сдвига.
Тензор деформации равен
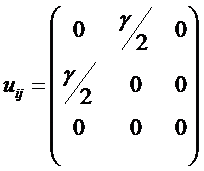
Тогда тензор скоростей деформации будет равен


Для одномерного течения Куэтта обозначают также τ = η dγ/dt
Ньютоновские и Неньютоновские жидкости:


1- ньютоновская
2- псевдопластическая жидкость – снижение кажущейся вязкости из-за распада частиц и др. явлений.
3- дилатантная жидкость – дезориентация частиц потоком, сухое трение
4- Вязкопластическая жидкость (вязкопластическое тело): модель Шведова-Бингама
dγ/dt = 0, если τ < τ0
τ = η dγ/dt + τ0, если τ > τ0
Лучше говорить о характере течения (вязкопластическое, псевдопластическое, дилатантное)
Графики для напряжения сдвига и кажущейся вязкости


1.3. Неньютоновские биологические жидкости
Уравнение Кэссона (Кассона).






Кровь, Желчь
Уравнения (законы сохранения) для многофазной и/или многокомпонентной сплошной среды
Уравнения баланса массы и импульса

+ уравнения баланса энергии, момента импульса
+ определяющие соотношения для потоков тепла, массы
+ реологические соотношения, связывающие тензоры напряжений и деформаций
Мягкие ткани: основные тензорные уравнения и свойства
1. Анизотропия
Для линейно-упругого анизотропного тела
 Всего 34 = 81 коэффициент
Всего 34 = 81 коэффициент  , из них 21 коэффициент независимый.
, из них 21 коэффициент независимый.
Энергия деформации

У изотропного тела есть только две упругие константы.
Тело Гука
σij = Kukk δij + 2μ(uij – 1/3 δijukk)
Уравнения движения