МИНИСТЕРСТВО ТРАНСПОРТА И КОММУНИКАЦИЙ
РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»
Кафедра «Архитектура»
Т. С. ТИТКОВА
ПОСТРОЕНИЕ ТЕНЕЙ
В ПЕРСПЕКТИВЕ
Учебно-методическое пособие
Гомель 2017
МИНИСТЕРСТВО ТРАНСПОРТА И КОММУНИКАЦИЙ
РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»
Кафедра «Архитектура»
Т. С. ТИТКОВА
ПОСТРОЕНИЕ ТЕНЕЙ
В ПЕРСПЕКТИВЕ
Одобрено методической комиссией факультета ПГС
в качестве учебно-методического пособия
Гомель 2017
УДК 514.18 (075.8)
ББК 22.151.3
Т45
Рецензенты:ст. преподаватель кафедры «Архитектура» И. В. Михальцова; ст. преподаватель кафедры «Промышленные и гражданские сооружения» О. Н. Коновалова (БелГУТ)
| Титкова, Т. С. Т45 Построение теней в перспективе: учеб.-метод. пособие / Т. С. Титкова; М-во транспорта и коммуникаций Респ. Беларусь, Белорус. гос. ун-т трансп. – Гомель: БелГУТ, 2017. – 22 с. ISBN 978-985-554-640-6 Учебно-методическое пособие содержит теоретические сведения по построению теней в перспективе, снабженные пояснениями и иллюстрациями, необходимыми для понимания материала. Предназначено для студентов специальности «Архитектура». УДК 514.18 (075.8) ББК 22.151.3 |
| ISBN 978-985-554-640-6 | © Титкова Т. С., 2017 |
| © Оформление. БелГУТ, 2017 |
ВВЕДЕНИЕ
Для придания перспективному изображению большей наглядности на нем строят тени, преимущественно принимая освещение солнечными лучами. Тени могут быть построены двумя способами. Первый заключается в том, что тени переносят на перспективу с ортогональных проекций в процессе построения самого перспективного изображения (достаточно трудоемкий), второй, наиболее распространенный, – в том, что тени строят непосредственно на перспективном изображении объекта.
Тени в перспективе могут быть построены при естественном (солнечном) или искусственном (лампочка) освещении.
ПОСТРОЕНИЕ ТЕНЕЙ ПРИ ЕСТЕСТВЕННОМ ОСВЕЩЕНИИ
Направление лучей. Положение источника света
Построение теней в перспективе и аксонометрии имеет много общего. Так же, как и в аксонометрии, для построения теней в перспективе необходимо иметь две проекции – перспективу луча и вторичную ее проекцию. Точки схода вторичных проекций лучей находятся на линии горизонта, так как источник света (Солнце) считается удаленным в бесконечность.
В зависимости от направления лучей и положения источника света относительно зрителя и картины возможны три основные схемы построения теней (рисунок 1).
|
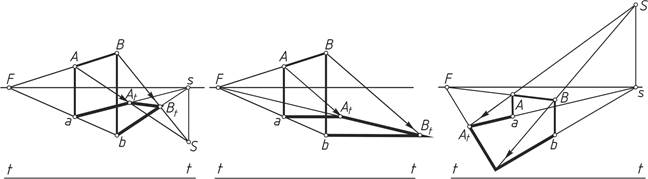
Рисунок 1 – Положение источника света:
а – позади зрителя, слева; б – лучи света параллельны картинной плоскости; в – перед зрителем, справа
На первой схеме солнце находится позади зрителя, слева. При этом точка схода проекций лучей s расположена на горизонте, а точка схода самих лучей (перспектива солнца) S – ниже горизонта на одной вертикали с точкой s.
На второй схеме лучи света параллельны картинной плоскости, поэтому они изображаются и на перспективе параллельными, а вторичные их проекции – параллельными основанию картины.
На третьей схеме солнце расположено перед зрителем, справа. Точка схода вторичных проекций лучей s находится на горизонте, а точка схода S перспектив лучей – выше горизонта.
При построении теней в перспективе наиболее часто применяют первое и второе направления лучей света, при которых изображенные на перспективе грани освещены.
Тень точки, прямой
Закономерности построения теней в ортогональных проекциях и аксонометрии в основном сохраняются и при построении теней в перспективе.
Тенью точки, падающей на плоскость или поверхность, является точка пересечения светового луча, проходящего через данную точку, с плоскостью или поверхностью. Поэтому построение точки сводится к решению основной позиционной задачи на построение точки пересечения прямой с плоскостью или поверхностью (рисунок 2, а). Тень точки А (А 
)на предметную плоскость определяется как точка пересечения перспективы луча AS, проходящей через данную точку, с вторичной проекцией as луча, проходящего через вторичную проекцию точки (а).
На рисунке 2, б изображена вертикальная прямая АВ. Точка А лежит в предметной плоскости, поэтому тень от нее совпадает с ее перспективой и вторичной проекцией. Тень от точки B (B )есть точка пересечения перспективы луча BS, проходящего через перспективу точки, со вторичной проекцией этого луча bs, проходящего через вторичную проекцию этой точки (b).
Таким образом, тень от вертикальной прямой всегда совпадает со вторичной проекцией луча.
На рисунке 2, в изображен отрезок прямой АВ, параллельный предметной плоскости. Перспектива и вторичная проекция такой прямой пересекаются на линии горизонта в точке F. Строят тени от точек А (А )и В (B ). Соединив тени от двух точек, получают тень от отрезка прямой, которая при продолжении проходит через точку F.
Вывод: если прямая параллельна предметной плоскости, то вторичная проекция луча и тень от нее сходятся в одной точке на линии горизонта.
а) б) в)
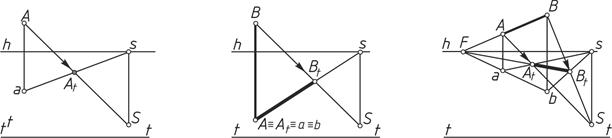
Рисунок 2 – Построение теней точки, прямой:
а – тень точки; б – тень вертикальной прямой; в – тень горизонтальной прямой
Рассмотрим особенности построения падающих теней от прямых на различных плоскостях.
Пример 1 (рисунок 3, а). Построить в перспективе тень от вертикальной прямой АВ на предметной плоскости и горизонтально проецирующей плоскости Р.
Точка В заданного отрезка лежит в предметной плоскости. Тень от точки В совпадает с ее перспективой. Тень от вертикальной прямой на предметной плоскости совпадает со вторичной проекцией луча. Для построения тени от точки А на плоскости Р строится линия пересечения вспомогательной плоскости Т, в которую заключается луч света, с плоскостью Р. Пересечение перспективы луча света AS с линией пересечения 1–2плоскостей Т и Р есть тень от точки А на плоскости Р (А ).
Из чертежа видно, что тень от вертикальной прямой на горизонтально проецирующей плоскости есть вертикальная прямая (параллельная заданной прямой).
Пример 2 (рисунок 3, б). Построить в перспективе тень от горизонтальной прямой АВ на горизонтально проецирующей плоскости Р,ей параллельной.
Так как прямая АВ параллельна предметной плоскости, то ее перспектива и вторичная проекция сходятся в точке F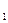 
, лежащей на линии горизонта. Тени от точек А и В на плоскости Р строят аналогично примеру 1. Вспомогательные плоскости, в которые заключают лучи света, не показывают (дважды решается задача на пересечение прямой с плоскостью). Соединив точки А и В , получают тень от прямой, которая при продолжении пройдет через точку F .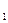
Вывод: перспектива отрезка горизонтальной прямой, его вторичная проекция и тень этого отрезка на горизонтально проецирующей плоскости, ему параллельной, сходятся в одной точке F, лежащей на линии горизонта.
а) б)
Рисунок 3 – Построение тени прямой:
а – вертикальной; б – горизонтальной
Пример 3 (рисунок 4). Построить в перспективе тень от горизонтальной прямой АВ на горизонтальной плоскости CDEK. Направление лучей света задано.
Рисунок 4 – Построение тени горизонтальной прямой на горизонтальную плоскость
Отрезок прямой АВ и плоскость заданы перспективой и вторичной проекцией. Так как параллельные между собой прямые АВ, CD и KE параллельны предметной плоскости, то их перспективы и вторичные проекции сходятся в точке F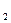 
, лежащей на линии горизонта. Стороны CK и DE параллельны предметной плоскости и между собой, поэтому имеют точку схода F 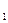на линии горизонта.
Для построения тени от точки А на горизонтальной плоскости CDEK необходимо:
1 Луч, проходящий через точку А, заключить мысленно в горизонтально проецирующую плоскость.
2 Определить линии пересечения этой плоскости с предметной плоскостью (прямая a 1), вертикальной плоскостью cCDd (прямая 1–1 ')и плоскостью CDEK (прямая 1 'A ); 1 'A // a 1.
3 Пересечение луча AA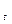 
с прямой 1 'A 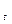есть искомая точка. Аналогично строится тень от точки В на эту же плоскость. Соединив тени точек А и В, получают тень от отрезка прямой на горизонтальной плоскости.
Тень от горизонтальной прямой в пространстве на плоскость, ей параллельную, параллельна самой прямой, поэтому в перспективе (при продолжении) пройдет через ту же точку схода F, что перспектива и вторичная проекция отрезка прямой.
Пример 4 (рисунок 5, а). Построить в перспективе тень от горизонтальной прямой АВ на горизонтально проецирующую плоскость Р. Направление лучей света задано.
Поскольку точка В принадлежит плоскости Р, тень от нее совпадает с самой точкой. Находим тень от точки А на пересечении перспективы светового луча и его вторичной проекции (А 
). Так как прямая АВ параллельна предметной плоскости, то ее тень по предметной плоскости пройдет через точку схода прямой F 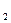. Точка 1 – точка излома тени.
Пример 5 (рисунок 5, б). Построить тень от вертикальной прямой АВ на наклонной плоскости Р. Поскольку прямая АВ вертикальная, тень от нее на предметной плоскости совпадает со вторичной проекцией луча (В 1). Мысленно заключаем световой луч во вспомогательную плоскость, которая пересекает плоскость Р по линии 1–2 '. Пересечение перспективы луча света AS с линией 1–2 ' и есть тень от точки А на плоскости Р (А ).
а) б)
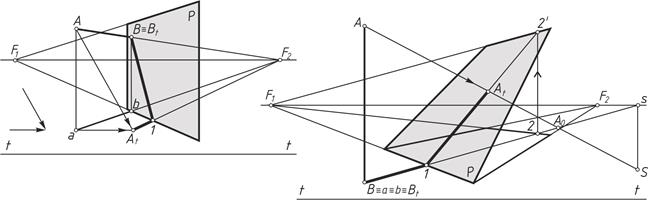
Рисунок 5 – Построение тени прямой:
а – фронтально проецирующей; б – вертикальной на наклонную плоскость
Пример 6 (рисунок 6). Построить тень от наклонной прямой АВ на наклонной плоскости Р.
|
). Тень от прямой АВ на предметной плоскости – отрезок В 
А . Мысленно заключают световой луч, проходящий через точку А, во вспомогательную плоскость, которая пересекает плоскость Р по линии 1–2 '. Пересечение перспективы луча света AS с линией 1–2 ' и есть тень от точки А на плоскости Р (А ).
Пример 7 (рисунок 7). Построить в перспективе тень от горизонтальной прямой АВ на две плоскости – вертикальную и горизонтальную. Направление луча света задано.
Строят тень от точки А на вертикальной плоскости и тень от точки В на горизонтальной плоскости CDEК. Так как перспектива горизонтальной прямой АВ и ее тень сходятся в одной точке F 
, проводят прямую через точки B 
и F до пересечения с линией CK, ограничивающей горизонтальную плоскость. Получают точку L . Соединив точки L и А , получают тень на вертикальной плоскости от горизонтальной прямой АВ.
При помощи обратного луча света, проведенного из точки L , можно определить границу участка прямой АВ, от которого тень падает на вертикальную, либо на горизонтальную плоскость.
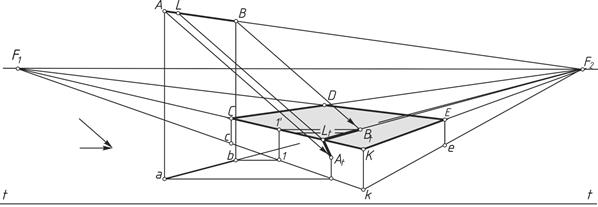
Рисунок 7 – Построение тени горизонтальной прямой на две плоскости
Тень плоской фигуры
Падающую тень от любой плоской фигуры можно построить как совокупность падающих теней точек и прямых, составляющих эту фигуру.
Пример 8 (рисунок 8, а). Построить тень от горизонтально проецирующей плоскости ABCD.
Поскольку точки С и D лежат в предметной плоскости, то тени от них совпадают с самими точками. Падающую тень дают стороны СВ, ВА, AD. Поскольку прямые СВ и AD вертикальные, то тени от них совпадают со вторичной проекцией луча. Прямая ВА – горизонтальная, следовательно тень от нее проходит через ту же точку схода, что и перспектива прямой (F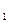 
).
Пример 9 (рисунок 8, б). Построить тень от наклонной плоскости ABCD. Направление лучей света задано.
Прямая AD принадлежит предметной плоскости, поэтому тень от нее совпадает с самой прямой. Находим тень от точки С, используя ее вторичную проекцию с. Луч света, проходящий через точку С, пересечется со своей вторичной проекцией сС в искомой точке С . Аналогично находим тень от точки В (В ). Соединяем поочередно найденные точки и получаем тень от плоскости ABCD (A B C D ).
а) б)
Рисунок 8 – Построение тени плоскости:
а – горизонтально проецирующей; б – наклонной
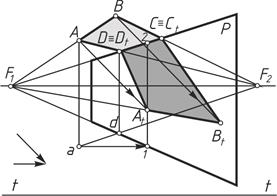Пример 10 (рисунок 9). Построить тень от горизонтальной плоскости ABCD на горизонтально проецирующую плоскость Р. Направление лучей света задано.
Плоскость ABCD пересекает плоскость Р по линии CD, тени точек C и D совпадают с самими точками.
|
. Проводим через точку А луч света, заключаем его в лучевую плоскость и находим А на вертикальной прямой 1–2 (линия пересечения плоскости Р с лучевой плоскостью). Тенью прямой АВ будет параллельная ей прямая, следовательно АВ и A B пересекутся в точке схода F 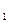. Соединяем теневые точки и получаем падающую тень D A B C .
Тени геометрических тел
При построении теней от объемных тел сначала определяется граница собственной тени, так как контур падающей тени есть тень от контура границы собственной тени. Для этого мысленно проводятся перспективы и вторичные проекции лучей света. Если они пересекаются с плоскостями или прямыми, ограничивающими их, то эти плоскости будут освещаться. Остальные плоскости будут находиться в собственной тени.
На рисунке 10, а параллелепипед стоит на предметной плоскости. Грани ABCK и CDEK находятся в собственной тени. Значит, границей собственной тени будет ломаная ABCDE.
На рисунке 10, б параллелепипед расположен над предметной плоскостью. В собственной тени находятся грани ABCK, CDEK, AFEК. Значит, границей собственной тени будет ломаная ABCDEFА.
а) б)
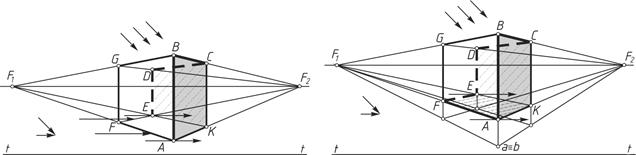
Рисунок 10 – Определение границы собственной тени параллелепипеда:
а – расположенного на предметной плоскости; б – расположенного над предметной плоскостью
Используя правила, рассмотренные выше, строятся тени от всех звеньев ломаной линии.
Пример 11 (рисунок 11). Построить падающую тень от параллелепипеда, расположенного на предметной плоскости.
Тень от отрезка прямой АВ совпадает со вторичной проекцией луча света (тень от вертикального отрезка). От отрезка прямой ВС тень при продолжении пройдет через точку схода F . Тень от отрезка прямой CD при продолжении пройдет через точку схода F 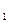. Тень от отрезка DE совпадает со вторичной проекцией луча света, как от любой вертикально расположенной прямой.
Пример 12 (рисунок 12). Построить падающую тень от параллелепипеда, расположенного над предметной плоскостью.
Для построения теней точек используется вторичная проекция параллелепипеда на предметной плоскости. Тень отрезка АВ совпадает с вторичной проекцией светового луча. Тень от отрезка ВС проходит через точку схода F , от отрезка CD – через точку схода F 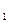как тени от горизонтальных прямых на горизонтальной плоскости. Тень от отрезка ED совпадает со вторичной проекцией луча как тень от вертикальной прямой. Тень от отрезка EF проходит через точку схода F , а от отрезка FA – через точку схода F 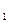как тени от горизонтальных прямых на горизонтальной плоскости.
Соединяем теневые точки и получаем падающую тень A B C D E F A .
Рисунок 11 – Построение падающей тени параллелепипеда, расположенного на предметной плоскости
Рисунок 12 – Построение падающей тени параллелепипеда, расположенного над предметной плоскостью
На рисунке 13 показано построение теней от двух пересекающихся призм. Сначала определяется контур собственной тени на обеих призмах (две ломаные ABCGg и EDМKk).
Тень от вертикального ребра АВ на предметной плоскости совпадает со вторичной проекцией луча (А 1), на вертикальной грани второй призмы – параллельна самому ребру (1–2 // АВ), на горизонтальной грани второй призмы – параллельна вторичной проекции луча (2 В ). Тень от ребра ВС будет направлена в точку F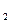 
, от ребра СG – в точку схода F 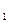как тень от горизонтальной прямой. Тень от вертикального ребра Gg совпадает со вторичной проекцией луча, расположенной на верхней грани низкой призмы.
Тень от низкой призмы строится аналогично построениям на рисунке 11. Тень от вертикального отрезка DE на предметной плоскости совпадает со вторичной проекцией луча, тени от горизонтальных отрезков DМ и МK направлены в точки схода самих отрезков: D М – в точку F 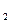, М K – в точку F .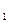
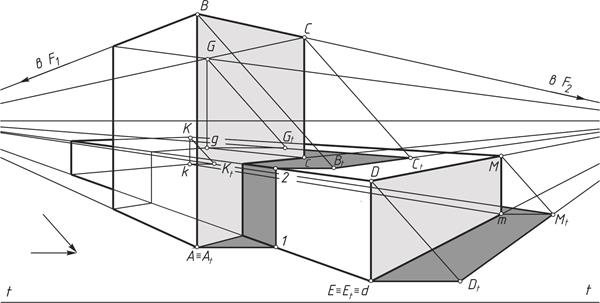
Рисунок 13 – Построение падающих теней от двух пересекающихся призм
На рисунке 14 показано построение теней от группы пересекающихся призм. Тень от ребра АВ строится аналогично построениям на рисунке 13. Часть тени от горизонтального ребра ВС на горизонтальной плоскости низкой призмы направлена в точку F 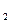(В 3). Далее тень идет по вертикальной плоскости mMPR средней призмы (3 L). Для того, чтобы ее построить, надо мысленно продлить плоскости АВСс и mMPR до пересечения (линия 1–2), соединить точки 2 и 3. Точка L – искомая точка тени. Далее тень от ребра АВ идет по горизонтальной плоскости MPNK средней призмы в точку схода F (LС ). Построение теней от остальных ребер понятно из чертежа.
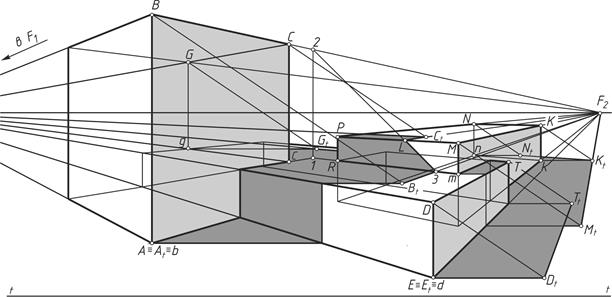
Рисунок 14 – Построение падающих теней от группы пересекающихся призм
Тень от наклонного ребра АВ на рисунке 15 падает на три плоскости. По предметной плоскости тень (А 3) идет в мнимую тень от точки В (В ). По вертикальной плоскости низкой призмы тень (3 L) проходит через точку 2 (линия 1–2 – линия пересечения плоскостей АВСсN 1 А и 1 EDN при мысленном их продлении). По горизонтальной плоскости низкой призмы тень проходит через точку В . Построение теней от остальных ребер понятно из чертежа.
Рисунок 15 – Построение падающих теней от группы пересекающихся призм
Тени цилиндра, конуса, шара. Чтобы построить падающую тень цилиндра (рисунок 16, а), сначала строят его собственную тень, проводя вторичные проекции лучей, касательные к основанию цилиндра (точки 1, 2). Падающую тень отбрасывают образующие 1–1' и 2–2' и часть окружности верхнего основания – линия 1'3'2'.
При построении теней конуса (рисунок 16, б) сначала строят падающую тень от вершины (С ) на плоскость его основания, затем через нее проводят касательные лучи к основанию конуса (С 1, С 2). Образующие 1 С и 2 С являются границей собственной тени конуса.
Для того, чтобы построить собственную тень шара (рисунок 16, в), необходимо провести через точку s касательные линии к экватору (точки 3, 4) и касательные к очерку через точку S (точки 1, 2). Эллипс 1–4–2–3 будет контуром собственной тени шара.
а) б) в)
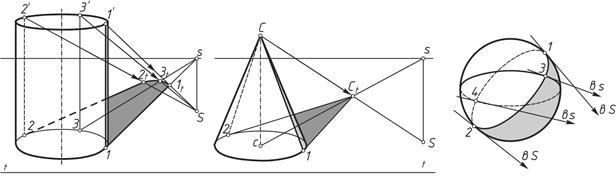
Рисунок 16 – Построение теней:
а – цилиндра; б – конуса; в – шара
Тени архитектурных деталей и фрагментов
Тени на лестнице от прямого барьера.
На рисунке 17 представлено построение тени на лестнице от прямого барьера при заданном направлении лучей света.
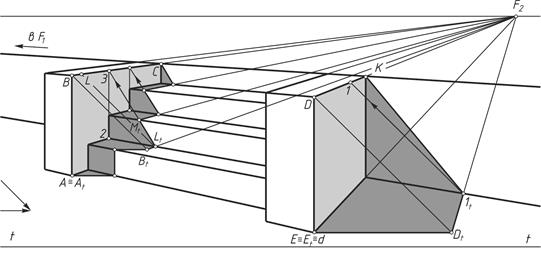
Рисунок 17 – Построение теней на лестнице от прямого барьера
Вначале строим тень от правого барьера. Тень от вертикального ребра DE на предметной плоскости совпадает со вторичной проекцией луча. Тень от горизонтального ребра DК на предметной плоскости направлена в точку схода F (D 
1 – реальная часть этой тени на предметной плоскости). Точка К принадлежит стене, поэтому тень отрезка 1 К падает на стену.
Рассмотрим построение тени от левого барьера. Тень от вертикальной прямой АВ на предметной плоскости и первой проступи параллельна вторичной проекции луча, на вертикальной плоскости нижнего подступенка параллельна самому ребру АВ. Точка В отбрасывает тень на первую проступь (В ).Далее строим тень от горизонтального ребра ВС. Часть его тени на первой проступи параллельна ребру и направлена в точку схода F 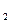(B L ). На вертикальной плоскости второго подступенка тень от ребра (L M ) строится с помощью линии 2–3 пересечения теневой плоскости барьера и плоскости подступенка. На остальных ступенях построения ведутся аналогично.
Тени на лестнице от наклонного барьера (рисунок 18).
Рисунок 18 – Построение теней на лестнице от наклонного барьера
Для построения падающей тени от боковой стенки лестницы на ступенях использован прием продолжения ребра, от которого строится тень (в данном случае ребро ВС), до пересечения с той гранью, на которой строится падающая тень.
Вначале строим тень от вертикальной прямой АВ, которая на предметной плоскости совпадает со вторичной проекцией луча (А В ). Далее строим тень от наклонного ребра ВС. Для этого продлеваем ребро ВС до пересечения с линией 1 А, принадлежащей предметной плоскости. Тень пройдет через точки 2 и В до первого подступенка (В 3). Далее продлеваем плоскость первого подступенка до пересечения с ребром ВС (линия 1–4). Тень пройдет через точки 3 и 4 (3–5). На оставшихся проступях и подступенках тень строится аналогично и заканчивается тенью от точки С (С ).
Тень от горизонтального ребра CD проходит через точку схода F .
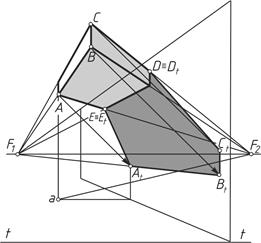
Тень от трубы на крышу (рисунок 19, а). Сначала определяют собственную тень трубы (ломаная ABCDE). Чтобы построить падающую тень, необходимо построить вторичную проекцию трубы. Тень от вертикального ребра АВ строится как на рисунке 5, б. Аналогично находят тень точки С. Тень от горизонтального ребра DE направлена в точку схода F , что и само ребро.
а) б)
в) г)
Рисунок 19 – Построение теней архитектурных деталей:
а – трубы; б – плиты балкона; в – плиты на столб; г – главки
На рисунке 19, б представлено построение тени от плиты балкона на плоскость стены. Падающую тень дают ребра, которые определяют границу собственной тени – EA, AB, BC, CD. Находят тень от точки А (А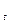 
). Тень от горизонтального ребра AB направлена в точку схода F 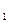, что и само ребро (А 
В ), тень от вертикального ребра BC падает вертикально.
Тень от квадратной плиты на призматический столб (рисунок 19, в) построена с использованием продолжения передней грани до пересечения с ребром АС в точке D.
Собственная тень главки (рисунок 19, г) построена аналогично собственной тени шара. Падающую тень от главки на цилиндрическую поверхность барабана главы строят с помощью вертикальных лучевых сечений. Точка 5 «исчезновения» тени может быть определена обратным лучом, проведенным из точки 5 
пересечения контуров падающих теней на предметной плоскости.
Тени цилиндрического столба с квадратной плитой (рисунок 20, а) строятся аналогично построению теней в аксонометрии. Сначала определяют собственную тень столба проведением вторичной проекции луча касательно к основанию столба.
Для построения контура падающей тени от двух горизонтальных ребер плиты выбраны характерные точки, которые определены вторичными проекциями лучей, проведенными в обратном направлении:
– точка В определена вторичной проекцией луча, касающейся верхнего основания цилиндра в точке, принадлежащей границе его собственной тени;
– точка С бросает тень на очерковую образующую цилиндра, здесь контур падающей тени касается очерка.
Построение тени точки А понятно из чертежа.
Тени цилиндрического столба с цилиндрической плитой (рисунок 20, б). Собственные тени круглой колонны и плиты найдены проведением горизонтальных проекций лучей, касательных на нижней плоскости плиты. Тень, падающая от плиты на столб, определена по точкам: 1 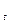– на очерке столба и 4 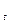– на границе собственной тени столба. Тень, падающая на землю, определена по точке В .
а) б)
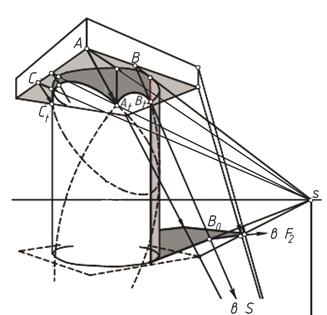
Рисунок 20 – Построение теней цилиндрического столба:
а – с квадратной плитой; б – с цилиндрической плитой
Тени в арочном проеме (рисунок 21). Тень в проеме определяется точками схода s и S. От вертикального ребра аА тень падает на предметную плоскость и частично на вертикальную стенку арки. Для построения тени, падающей от криволинейной части контура арки, находим положение точки s ' – точки схода перспектив проекций световых лучей на плоскости стены арки. Для этого из точки схода F 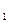через точку А проводим прямую до пересечения ее с контуром арки в точке 1. Тогда прямая, соединяющая точки А и 1 в пересечении с перпендикуляром, восстановленным к линии горизонта в точке F 
, определит искомую точку s '.
Для построения тени от любой точки арки, например от точки В, проводим через эту точку проекции луча в точки s ' и S. Отметив на контуре арки в пересечении с лучом точку 2, проводим из нее прямую в точку схода F 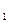. В пересечении проведенной прямой с лучом ВS найдем искомую тень В .
Касательная, проведенная к очерку арки из точки s ', определяет точку C – крайнюю точку тени и границу собственной тени CC .
Рисунок 21 – Тени в арочном проеме
Тени карниза (рисунок 22).Чтобы построить собственные и падающие тени, необходимо построить лучевое сечение профиля карниза. Для этого в произвольном месте карниза проводят вертикальный отрезок, на который переносят членения карниза. Через точки 1, …, 4 проводят прямые в точку схода s проекций лучей до пересечения с соответствующими прямыми профиля карниза и вычерчивают лучевое сечение 1–2–3 –4 –5 –6 –7 . В плоскости сечения в точку S проводят луч, касательный к построенному сечению (точка 8), и определяют контур собственной тени выкружки. Через точки 2, 4 
проводят лучи в точку S и определяют контуры падающих теней на профиле карниза (точки 9, 10).
Падающая тень на стену строится по алгоритму решения задачи на пересечение прямой с плоскостью. Для построения тени от точки А проводят через эту точку вспомогательную вертикальную лучевую плоскость ASs, которая пересекает «потолок» по линии АА , а стену по линии А А . Точка А – искомая тень от точки А на стене. Тень от вертикального отрезка АВ падает на стену вертикально (А В ). Участок ВС нижнего ребра плиты дает тень на стену, параллельную самому отрезку (В С идет в точку схода F ). 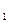Далее строят тень от точки D аналогично построению тени от точки А, получают тень от линии профиля С D (С D ). Затем строят тени от участка ЕD горизонтального ребра, вертикального отрезка Е К, горизонтального ребра KG.
Рисунок 22 – Тени карниза
Тени схематизированного здания. В случае наличия в здании скатной кровли может оказаться спорным вопрос: находится ли скат (наклонная плоскость) в собственной тени или попадает под световые лучи.
На рисунке 23 показаны три случая положения теней