Основы логики
Задача
Какая из логических операций не будет иметь истинного значения, когда на входе операции все аргументы истинны? В ответе укажите номер операции в списке.
1. Импликация
2. Дизъюнкция
3. Конъюнкция
4. Исключающее ИЛИ
Задача
Четыре года подряд Коля, Сережа, Ваня и Петя ходили в походы в мае, июне, июле и августе. Каждый мальчик по одному разу был в походе в каждый из перечисленных месяцев, при этом не было такого года, чтобы в один и тот же месяц в поход пошли сразу несколько мальчиков. В первый год Ваня ходил в поход в июле, а во второй - в августе. Во второй год в мае в поход ходил Коля. На третий год в июне в поход ходил Петя, а на четвертый год в июле в поход ходил Сережа. В каком месяце ходил в поход Сережа в первый год? В ответе укажите название месяца маленькими буквами в именительном падеже.
Задача
Для логической функции F(X,Y,Z) известен фрагмент таблицы истинности.
| X | Y | Z | F |
Какие из предложенных выражений соответствуют функции F? В ответе укажите в порядке возрастаний номера соответствующих выражений через запятую.
1) not (X and Y) and Z
2) not (X or not Y) or Z
3) not (X and Y) or Z
4) (X or Y) and Z
5) not (X or Z) or not Y
Задача
Три школьника из трех различных городов приехали на отдых в один лагерь. На вопрос вожатого, из каких городов они приехали, каждый дал ответ. Петя: «Я приехал из Тольятти, а Леня — из Самары». Леня: «Нет, это я приехал из Тольятти, а Петя — из Екатеринбурга». Коля: «Из Тольятти приехал я, а из Екатеринбурга приехал Леня». Вожатый, удивленный противоречиями в ответах ребят, попросил их объяснить где, правда, а где ложь. Тогда ребята признались, что в ответе каждого из них одно утверждение верно, а другое — ложно. Перечислите через запятую сначала имя мальчика, который приехал из Тольятти, затем имя мальчика, который приехал из Самары и затем имя мальчика, который приехал из Екатеринбурга.
.
| 5. Задача |
В соревнованиях планировали участвовать три атлета (A, B, C). После начала соревнований стало известно, что следующие высказывания являются истинными:
1. Атлет A участвует в соревнованиях, а атлет B — не участвует.
2. Неверно, что из двух атлетов B и C в соревнованиях участвует только один. Определите, какие атлеты в результате приняли участие в соревнованиях. В ответе укажите через запятую латинские буквы, обозначающие атлетов.
Задача
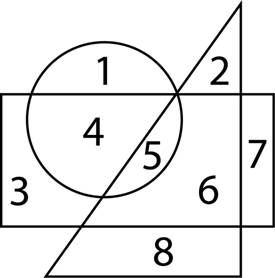
Высказывания A, B, C истинны только для точек, принадлежащих кругу, треугольнику и прямоугольнику соответственно. На схеме цифрами обозначены непересекающиеся области. Напишите через запятую в порядке возрастания номера областей, в которых будет истинным выражение: (B andnot C) or C and (A ↔ B)
7. Задача
Четыре брата (Федор, Иван, Петр и Григорий) купили игровую приставку. Одновременно играть на приставке может только один человек. Пытаясь решить, как поделить время использования приставки, каждый брат обозначил по два временных промежутка, в которые он мог бы играть. Федор хочет играть утром или днем, Иван — днем или вечером, Петр — утром или ночью, Григорий — вечером или ночью. Подберите варианты распределения времени, которые устроили бы всех братьев. Если вариантов несколько, укажите в ответе их коды через запятую. Если вариант один — укажите в ответе его код. Код каждого варианта формируется следующим образом: первые буквы имен братьев пишутся подряд без пробелов в порядке следования временных промежутков: утро, день, вечер, ночь.
Задача
Высказывания A, B, C истинны только для точек, принадлежащих прямоугольнику, кругу и звезде соответственно (А – квадрат, В - круг, C – звезда). Какая из диаграмм Эйлера-Вена эквивалентна выражению:
(A or (not A and B)) and ((not B and C) or C)
В ответ введите число от 1 до 12, соответствующее номеру правильной диаграммы. Варианты ответов:
1. 
| 4. 
| 7. 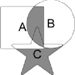
| 10. 
|
2. 
| 5. 
| 8. 
| 11. 
|
3. 
| 6. 
| 9. 
| 12. 
|
Задача
При выполнении какой из перечисленных побитовых логических операций над двумя многозначными двоичными операндами результатом будет многозначное двоичное число, значение которого не менее большего из аргументов?
Дизъюнкция
Импликация
Исключающее ИЛИ
Конъюнкция
Эквивалентность
Задача
В летний детский лагерь отдыха приехали ребята разных возрастов и их определили по трем отрядам: первый отряд – ребята 10-11 лет, второй отряд – 12-13 лет и третий отряд – 14-15 лет. Известно, что во втором отряде мальчишек в два раза больше, чем девчонок этого же отряда, и их количество (мальчишек 12-13 лет) составляет треть всех ребят лагеря (мальчиков и девочек). Также известно, что девочек во втором отряде на 5 меньше, чем в первом или третьем. Сколько всего мальчишек в первом и третьем отрядах, если всего в лагерь приехали 84 ребенка.
Задача.
Имеется логический исполнитель, которому на вход подаются два десятичных аргумента А и В. Исполнитель переводит аргументы в четырехразрядные двоичные операнды и может выполнять следующие команды:
1 – выполняет операцию побитового логического умножения двух операндов А и В, результат записывает в А;
2 – выполняет операцию побитового логического сложения двух операндов А и В, результат записывает в В;
3 – выполняет побитовую логическую операцию «исключающее ИЛИ» двух операндов А и В, результат записывает в В;
4 – выполняет побитовую инверсию операнда В, результат записывает в А.
На вход исполнителю подали десятичные аргументы А = 8 и В = 5. Найдите, сумму операндов А и В после выполнения программы { 3124 }. Результат запишите в десятичной форме. В ответе укажите целое число.
Задача
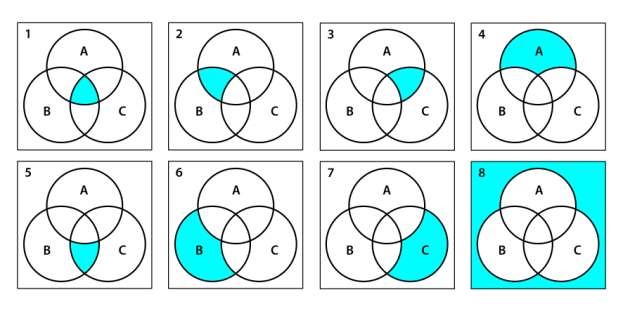
Дана логическая функция от трех переменных:
F(A, B, C) = (A or not B) -> C
Известно, что эту же функцию можно представить как дизъюнкцию нескольких функций из набора, который представлен ниже в виде диаграмм Эйлера-Венна. Выпишите в ответ через пробел в порядке возрастания номера функций, дизъюнкция которых будет эквивалентна исходной функции. На диаграммах цветом выделены области, в которых соответствующая функция принимает истинное значение.
Задача 9 – логика, таблицы истинности – 1 балл
Задан фрагмент таблицы истинности для логической функции F(A, B, C).
| A | B | C | F(A, B, C) |
Выберите среди перечисленных ниже ту логическую функцию, которая не будет противоречить этому фрагменту таблицы истинности.
1. A and B and C
2. not A and not B and C
3. A and B and not C
4. not A and not B and not C
5. A or B or not C