Введение. (см. Методические указания)
Векторы, действия над векторами. Координаты вектора.
Практическое занятие№1.Основные задачи, решаемые координатным способом.
Некоторые физические величины (скорость, сила, ускорение) характеризуются не только числовым значением, но и направлением. Например, чтобы охарактеризовать движение тела в данный момент, недостаточно указать скорость движения, а нужно указать и направление движения тела, т.е. направление скорости. Таким образом, скорость является векторной величиной. Другими примерами векторных величин могут служить сила притяжения, центробежное ускорение и т.п.
Если на некотором отрезке задано начало отрезка и его конец, то такой отрезок называется направленным.
Определение 1.
Вектором называется направленный отрезок прямой, т.е. отрезок, у которого одна из ограничивающих его точек принимается за начало, а другая - за конец.
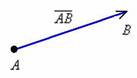
В данном случае началом отрезка является точка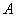 
, концом отрезка – точка 
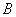. Сам вектор обозначен через 
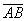. Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор 
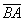, и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института или выйти из дверей института – это совершенно разные вещи. Вектор можно отложить от любой точки:
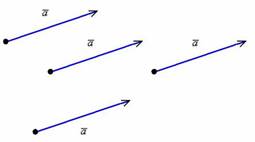
Определение 2.
Длиной или модулем вектора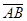 
называется длина отрезка АВ и обозначается 
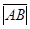. Если вектор 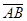обозначается через а, то его модуль обозначается 
.
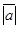Определение 3.
Вектор, начало и конец которого совпадают, называется нулевым вектором. Нулевой вектор обозначается 0. Модуль нулевого вектора равен нулю.
|
|
Определение 4.
Направлением вектора 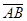называется направление, определяемое полупрямой АВ. Нулевой вектор направления не имеет.
Определение 5.
Векторы 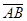и 
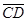называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены лучи AB и CD.
Определение 6.
Два ненулевых вектора называются коллинеарными, если они одинаково или противоположно направлены. Нулевой вектор считается коллинеарным любому вектору.
Определение 7.
Ненулевые векторы называются компланарными, если они параллельны одной и той же плоскости.
Определение 8.
Углом между двумя ненулевыми векторами a и b называется угол между направлениями этих векторов. Этот угол обозначается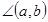 
.
Определение 9.
Два вектора называются равными, если они одинаково направлены и имеют одну и ту же длину.
Линейные операции над векторами.
1. Сложение векторов.
а) Правило треугольника.
+ 
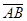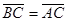
б) Правило параллелограмма.
 |
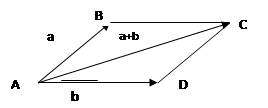Сложение векторов обладает следующими свойствами:
Свойство коммутативности: a+b=b+a,
Свойство ассоциативности: (a+b)+с= (a+b)+c,
Свойство «поглощения» нулевого вектора: а+0=а.
2. Вычитание векторов.
Для вычитания векторов их строят из одной точки, соединяют концы и ставят стрелку в сторону уменьшаемого.
 |
| |||
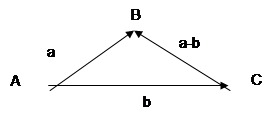3. Умножение вектора на число.
Произведением вектора а на число l называется вектор, длина которого равна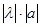 
, а направление совпадает с направлением вектора а, если l>0и противоположно вектору а, если l<0.
|
|
Операция умножения вектора на число обладает следующими свойствами:
Свойство ассоциативности относительно числовых множителей:
a(bа)=(ab)а
Свойство дистрибутивности векторного множителя относительно операции сложения чисел:
(a+b)а=aа+bа
Свойство дистрибутивности числового множителя относительно операции сложения векторов:
a (a+b) =aa+ab
1. Линейной комбинацией векторов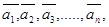 
называется сумма произведений этих векторов на какие-либо числа k1,k2,k3,…kn.. Справедливо следующее утверждение: любой вектор плоскости может быть представлен единственным способом в виде линейной комбинации неколлинеарных векторов 
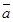и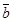 
, т. е. 
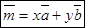. Говорят, что вектор 
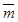разложен по векторам 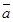и 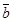. Базисом на плоскости называется пара неколлинеарных векторов, взятых в определённом порядке.
2. Скалярное произведение векторов.
Скалярным произведением двух отличных от нуля векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
.
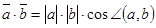Основные свойства скалярного произведения:
1. Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
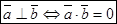
2. Скалярный квадрат вектора равен квадрату его длины.
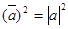
Декартова система координат.
Прямоугольная система координат определяется заданием прямоугольного базиса (i,j) и точки О; i- единичный вектор оси абсцисс (Ох); j- единичный вектор оси ординат (Оу).
Если в качестве базиса взять два взаимно перпендикулярных единичных вектора i и j, то говорят, что вектор разложен в декартовой системе координат (по имени её создателя Рене Декарта). Точка пересечения прямых, проведённых через указанные векторы, называется началом координат, а сами прямые - осями координат. Горизонтальная ось называется осью абсцисс, а вертикальная - осью ординат.
|
|
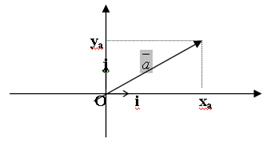
Координаты вектора
Так как любой вектор плоскости можно разложить единственным образом по базисным векторам, то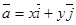 
. Коэффициенты х и у называются координатами вектора в данной системе координат.
Если вектор выходит из начала координат, то его координатами называют координаты конца этого вектора.
Если вектор задан координатами конца и начала (начало не совпадает с началом координат), то для нахождения координат вектора из координаты конца вычитают соответствующую координату начала.
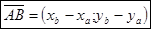
Запомни!
Координатами вектора являются координаты его конца при условии, что начало вектора совпадает с началом координат.
Если вектор задан координатами конца и начала, то для нахождения координат вектора из координаты конца вычитается соответствующая координата начала.
Если векторы равны, то их координаты тоже равны.
Действия над векторами в координатной форме.
При сложении (вычитании) векторов соответствующие координаты складываются (вычитаются).
При умножении вектора на число каждая координата умножается на это число.
Скалярное произведение векторов равно сумме произведений соответствующих координат: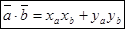 
Пример.
Даны д точки плоскост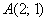и 
и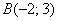 
. Найти координаты вектора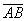
Решение: по соответствующей формуле: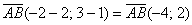 
Пример.
Даны векторы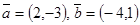 
. Найти координаты вектора 
.
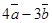Решение:
Сначала найдём координаты векторов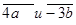 
, а затем сложим эти векторы.
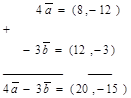
Формула нахождения длины вектора (абсолютной величины вектора):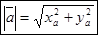 
Или
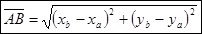, есливектор задан координатами конца и начала.
Формула нахождения угла между векторами:
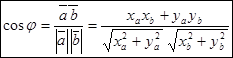
Основные формулы для решения задач координатным способом:
 |
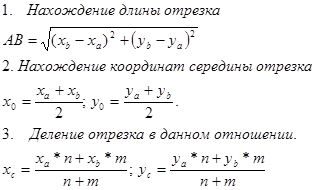
A (xa,ya) m C n B (xb,yb)
Пример 1.
Вычислить расстояние между точками М и К, если М(-5,7) и К(7,-9).
Решение:
Найдём длину отрезка по формуле:
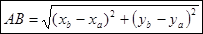
Тогда
МК=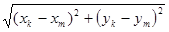 
= 
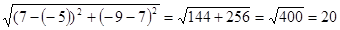
Пример 2.
В треугольнике АВС А(2,2), В(-1,6) и С(-5,3).Найти длину медианы АМ.
Решение:
Пример 3.
Даны точки В(-3,1) и С(8,-12). Найти координаты точек М и N, которые делят отрезок на три равные части.
Решение:
Вопросы и упражнения для самоконтроля:
1. Что называется вектором? Абсолютной величиной вектора? Нулевым вектором?
2. Дайте определение коллинеарных векторов.
3. Дайте определение равных векторов.
4. Как найти координаты вектора, заданного парой несовпадающих точек?
5. Как найти длину вектора?
6. Дать определение скалярного произведения векторов.
7. Написать формулу для вычисления скалярного произведения двух векторов по их координатам.
8. Сформулировать условие коллинеарности двух векторов.
9. Сформулировать условие перпендикулярности двух векторов.
10. Напишите формулу для вычисления угла между векторами.
11. Как найти расстояние между двумя точками?
12. Как найти координаты середины отрезка?
13. Вычислить скалярное произведение векторов:
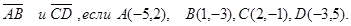
14. Вычислить угол между векторами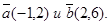 
15. Докажите, что треугольник с вершинами А(-1, 6), В(-5,3), С(-2,-1) –равнобедренный.
16. Найти конец В отрезка АВ, если даны его начало А(2,3) и середина С(4,9).
17. Найти на конце отрезка АВ точку С, делящую отрезок АВ в отношении АС:СВ=7:5, если А(2,9), В(-4,3).
Решить самостоятельно:
В треугольнике АВС найти: - периметр;
- медиану ВD;
- координаты точки пересечения медиан, если:
| А | В | С | |
| (4,-5) | (-1,2) | (0,8) | |
| (3,5) | (-2,9) | (1,6) | |
| (-5,1) | (7,-4) | (3,-2) | |
| (6,-2) | (-1,8) | (-1,2) | |
| (3,-2) | (4,-3) | (-1,0) | |
| (0,-7) | (4,-5) | (-3,9) | |
| (7,-4) | (0,-4) | (2,-6) | |
| (-1,2) | (6,-2) | (-4,7) | |
| (-1,0) | (-5,1) | (4,-5) | |
| (-1,8) | (0,8) | (4,-3) |