Глава 1. МЕТОД ЖОРДАНОВЫХ ИСКЛЮЧЕНИЙ

1.1. Метод обыкновенных жордановых исключений

Рассмотрим систему линейных уравнений:

(1.1)

В данной системе – постоянные коэффициенты (i = 1, 2,…, m; j = 1, 2,…, n).

Рассмотрим следующее преобразование данной системы, называемое в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную и подставим во все оставшиеся равенства. Это возможно только в том случае, когда 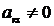. Коэффициент будем называть разрешающим элементом. После выражения и подстановки получаем новую систему (1.2), эквивалентную системе (1.1):

(1.2)

Чтобы определить коэффициенты системы (1.2) необходимо выразить их через коэффициенты исходной системы. Начнем с r -го уравнения, которое после выражения переменной x_s через остальные переменные будет выглядеть следующим образом:

(1.3)

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.4)

Вычислим новые коэффициенты b_ij (i ¹ r) произвольного (i -го) уравнения:

Раскрывая скобки и приводя подобные члены получим:

(1.5)

То есть коэффициенты системы (1.2), не вошедшие в разрешающую строку, вычисляются по формулам (1.6):

(1.6)

Таким образом, при совершении одного шага метода обыкновенных жордановых исключений (то есть, при переходе от системы (1.1) к системе (1.2)) коэффициенты пересчитываются по формулам (1.4) и (1.6).

Как и в случае решения линейных уравнений, методом Гаусса, преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых». Например, для исходной системы жорданова таблица будет выглядеть так:

Табл. 1.1

	x ₁	x ₂	…	x_j	…	x_s	…	x_n
y ₁	a ₁₁	a ₁₂		a _{1 j}		a _{1 s}		a _{1 n}
…………………………………………………………………..
y_i	a_i ₁	a_i ₂		a_ij		a_is		a_in
…………………………………………………………………..
y_r	a_r ₁	a_r ₂		a_rj		a_rs		a_rn
………………………………………………………………….
y_n	a_m ₁	a_m ₂		a_mj		a_ms		a_mn

Разрешающий элемент для наглядности выделим жирным шрифтом. Строку, в которой он находится, называют разрешающей строкой. Столбец, соответственно, разрешающим столбцом. В верхней строке записываются независимые элементы . В левый столбец – зависимые переменные . При переходе от таблицы 1.1 ко таблице 1.2 (и к каждой следующей) одна независимая переменная из верхней строки меняется местами с зависимой переменной из левого столбца (для разрешающего элемента переменная меняется местами с ).

Табл. 1.2

	x ₁	x ₂	…	x_j	…	y_r	…	x_n
y ₁	b ₁₁	b ₁₂		b _{1 j}		b _{1 s}		b _{1 n}
…………………………………………………………………..
y_i	b_i ₁	b_i ₂		b_ij		b_is		b_in
…………………………………………………………………..
x_s	b_r ₁	b_r ₂		b_rj		b_rs		b_rn
y_n	b_m ₁	b_m ₂		b_mj		b_ms		b_mn

1.2. Метод модифицированных жордановых исключений

При решении задач линейного программирования симплекс методом чаще используется модифицированный метод жордановых исключений. При этом метод обыкновенных жордановых исключений используется для решения двойственных задач (свойственный симплекс-метод). Отличие модифицированного метода жордановых исключений от метода обыкновенных жордановых исключений заключается в том, что свободные переменные системы уравнений берутся со знаком «минус». Т.е. один шаг модифицированного метода жордановых исключений заключается в преобразовании системы (1.7) к системе (1.8) с разрешающим элементом :

(1.7)

(1.8)

Нетрудно показать, что при совершении одного шага метода модифицированных жордановых исключений (то есть, при переходе от системы (1.7) к системе (1.8)), коэффициенты пересчитываются по формулам (1.9):

(1.9)

Решение задач, связанных с преобразованием систем линейных уравнений (в частности, задач линейного программирования) методом модифицированных жордановых исключений оформляется, как и для метода обыкновенных жордановых исключений, в виде жордановых таблиц. При этом исходной системе (1.7) соответствует таблица 1.3:

Табл. 1.3

	– x ₁	– x ₂	…	– x_j	…	– x_s	…	– x_n
y ₁	a ₁₁	a ₁₂		a _{1 j}		a _{1 s}		a _{1 n}
…………………………………………………………………..
y_i	a_i ₁	a_i ₂		a_ij		a_is		a_in
…………………………………………………………………..
y_r	a_r ₁	a_r ₂		a_rj		a_rs		a_rn
………………………………………………………………….
y_n	a_m ₁	a_m ₂		a_mj		a_ms		a_mn

Системе (1.8) соответствует таблица 1.4, в которой свободная переменная меняется с базисной не только местами, но и знаками:

Табл. 1.4

	– x ₁	– x ₂	…	– x_j	…	– y_r	…	– x_n
y ₁	b ₁₁	b ₁₂		b _{1 j}		b _{1 s}		b _{1 n}
…………………………………………………………………..
y_i	b_i ₁	b_i ₂		b_ij		b_is		b_in
…………………………………………………………………..
x_s	b_r ₁	b_r ₂		b_rj		b_rs		b_rn
………………………………………………………………….
y_n	b_m ₁	b_m ₂		b_mj		b_ms		b_mn

Впервые при решении задач линейного программирования метод жордановых исключений применил в 1947 году швейцарский математик Эдуард Штифель. В дальнейшем при решении задач линейного программирования мы будем использовать только модифицированный метод, который будем называть просто методом жордановых исключений или методом Штифеля.

1.3. Алгоритм решения задачи линейного программирования методом жордановых исключений

Общей задачей линейного программирования называется задача нахождения максимума или минимума линейной функции

, (1.10)

определенной на некотором выпуклом подмножестве (многограннике) n -мерного пространства, совпадающим с множеством решений некоторой системы ограничений (1.11):

, (1.11)

Если все ограничения системы (1.11) являются равенствами и все переменные x_i ограничены на знак (), то задача называется канонической, а если все ограничения системы (1.11) являются неравенствами и при этом все переменные ограничены на знак, то задача называется стандартной.

Функция (1.10) называетсяцелевой функцией. Любое решение системы ограничений (1.11), включая ограничения переменных на знак, называется планом задачи. План, на котором функция цели достигает своего максимума (минимума), называется оптимальным. Задача линейного программирования может иметь единственное решение (единственный оптимальный план), бесчисленное множество решений или вообще не иметь решений. Причем задача может не иметь решений или из-за отсутствия планов (несовместности системы ограничений) или из-за неограниченности целевой функции.

Множество планов, если оно не пусто, является выпуклым многогранником. Крайние точки (вершины) многогранника называются опорными планами. Известно, что если задача имеет единственный оптимальный план, то он совпадает с одним из опорных планов (линейная функция достигает максимума или минимума в одной из крайних точек многогранника). Если задача имеет бесчисленное множество оптимальных планов, то, по крайней мере, два из них совпадают с опорными планами.

Так как система (1.11) содержит лишь конечное число ограничений, то число опорных планов так же конечно. Данное обстоятельство позволило разработать специальный метод решения задач линейного программирования (симплекс-метод), основанный на переборе опорных планов и позволяющий за конечное число шагов найти решение задачи (оптимальный опорный план).

Идея симплекс-метода заключается в следующем:

1. Симплекс-методпозволяет за конечное число шагов найти первоначальный опорный план или доказать, что задача не имеет решения из-за отсутствия планов.

2. Симплекс-метод за конечное число шагов позволяет найти оптимальный опорный план или установить неограниченность целевой функции. Причем на каждом шаге значение функции цели улучшается (увеличивается, если задача на максимум).

Обычно симплекс-методом решаются канонические задачи. Задачи, содержащие не более трех переменных можно решать геометрически. Существуют способы перехода от общей задачи к канонической или к стандартной задаче. Однако они связаны с неоправданным увеличением количества переменных и ограничений (размерности задачи). Кроме того, при использовании стандартного симплекс-метода часто приходится использовать метод искусственного базиса, что так же приводит к увеличению ее размерности.

При использовании метода Штифеля (т.е. симплекс-метода, основанного на методе модифицированных жордановых исключений) мы можем решить любую общую задачу линейного программирования, не сводя ее к канонической задаче. Все дело в том, что в отличие от стандартного симплекс-метода, основанного на методе Гаусса-Жордана, основными задачами, решаемыми методом Штифеля, являются не канонические, а стандартные задачи. Наличие же в задаче особенностей, отличающих ее от стандартной задачи, лишь упрощает ее решение (уменьшается количество переменных и ограничений).

Алгоритм решения общей задачи линейного программирования оформляется в виде жордановых таблиц, и его можно разбить на три основных этапа:

1. Этап упрощения задачи. На данном этапе методом жордановых исключений из системы ограничений исключая равенства, что приводит к соответствующему уменьшению количества столбцов жордановой таблицы. При этом из таблицы последовательно исключаются неограниченные на знак переменные, что приводит к соответствующему уменьшению количества строк жордановой таблицы.

2. Этап выхода в область планов задачи. На данном этапе методом жордановых исключений мы находим первоначальный опорный план задачи, или доказываем, что задача не имеет планов (т.е., что система (1.11) – не совместна).

3. Этап нахождения оптимального опорного плана задачи. На данном этапе методом жордановых исключений мы находим оптимальный опорный план задачи или доказываем, что задача не имеет решения из-за неограниченного роста целевой функции.

Подробно все эти этапы были изучены в работах [1], [2].Рассмотрим данные этапы на примере конкретной задачи:

Пример 1.1. Требуется найти максимум функции

, (1.12)

при условии выполнения следующих ограничений

(1.13)

Сначала запишем условие задачи в виде жордановой таблицы. Для этого преобразуем систему (1.13) следующим образом.

(1.14)

При таком преобразовании все ограничения становятся равенствами, но при этом появляются добавочные переменные .

Теперь запишем задачу (1.12), (1.14) в виде жордановой таблицы:

Табл.1.5

-	-	-	-
			-2
	-2
-3			-2
-5			-2

В таблице 1.5 последняя строка отводится для коэффициентов целевой функции, которые берутся с противоположным знаком (если задача на «максимум».

1. Этап упрощения задачи. Выберем в качестве разрешающего элемента элемент , стоящей на пересечении базисной компоненты и свободной компоненты , не ограниченной на знак. После такого преобразования второй столбец можно исключить из таблицы. Мы приходим к таблице 1.6:

Табл.1.6

-	-	-
	-11		-20
-5		-1
-3		-2
	-11		-36

Строку, соответствующую неограниченной на знак переменной , можно, после предварительного запоминания из жордановой таблицы исключить. Получим таблицу:

Табл.1.7

-	-	-
	-11		-20
-5		-1
	-11		-36

Мы получили базисное решение задачи . Причем базисная компонента . Таким образом, полученное ними базисное решение системы ограничений не является планом нашей задачи (т.к. не выполняется одно из ограничений на знак).

2. Этап выхода в область планов задачи. Для выхода в область планов задачи, нам необходимо избавиться от отрицательных элементов правого столбца таблицы 1.7. В соответствии с [2] мы должны выбрать разрешающий элемент во втором столбце, содержащем отрицательный элемент напротив отрицательной правой части .

В дальнейшем мы в разрешающем столбце будем выбирать разрешающий элемент в соответствие с теоремой о минимальном симплексном отношении [2]. Симплексные отношения для элементов второго столбца таблицы 1.7 равны Минимальное из них приходится на первую строку, поэтому в качестве разрешающего элемента выбираем элемент . После пересчета получим таблицу:

Табл.1.8

-	-	-
-1	-1/11	-4/11	20/11

-4	-1		-16

Так как все элементы правого столбца неотрицательны, то таблице 1.8 соответствует первоначальный опорный план: 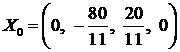. Добавочные компоненты и не выписаны, т.к. они носят вспомогательный характер, но при этом они обязаны оставаться неотрицательными. Компонента найдена из запомненной 3-ей строки таблицы 1.6. нас не должно смущать то обстоятельство, что , т.к. данная переменная не ограничена на знак. Значение целевой функции на первоначальном опорном плане равно . Так как среди оценок свободных переменных присутствуют отрицательные числа и , то, в соответствии с [2] делаем вывод, что первоначальный план не является оптимальным.

3. Этап нахождения оптимального опорного плана задачи. Выберем в качестве разрешающего столбца – первый столбец таблицы 1.8, т.к. именно он содержит наименьшую отрицательную оценку . Разрешающим элементом в данном столбце может быть только элемент , т.к. только для него существует симплексное отношение [2]. После пересчета получим таблицу:

Табл.1.9

-	-	-
1/6	5/66	3/22	71/33
1/6	1/6	1/2	1/3
2/3	-1/3		-44/3

Новый опорный план , соответствующий таблице 1.9 мы выписывать не будем, т.к. он (как и предыдущий опорный план ) не является оптимальным. Об этом говорит наличие отрицательной оценки во втором столбце. Однако заметим, что при переходе от плана к плану значение целевой функции возросло и слало равным .

Сделаем еще один шаг методом жордановых исключений, выбрав в качестве разрешающего столбца – второй столбец. Для выбора разрешающего элемента в нем вычислим симплексные отношения: . Так как второй строке соответствует наименьшее симплексное отношение, т выбираем в качестве разрешающего элемента элемент . После пересчета приходим к таблице:

Табл.1.10

-	-	-
1/11	-5/11	-1/11

			-14

Анализируя полученную таблицу, мы можем сделать вывод, о том, что ей соответствует оптимальный опорный план, причем данный опорный план является единственным оптимальным планом задачи. Об этом говорит то обстоятельство, что все оценки свободных переменных строго больше нуля.

Приравнивая свободные переменны к нулю, а базисные к элементам правого столбца, получим координаты оптимального плана.

Компонента найдена из запомненной 3-ей строки таблицы 1.6после подстановки в нее других компонент опорного плана. Максимальное значение целевой функции равно .

В приведенном примере с помощью жордановых таблиц решалась задача на «максимум». Задачу на «минимум» можно решать как задачу на «максимум», если поменять знаки целевой функции на противоположные. То есть, если требуется найти минимум функции

То при той же системе ограничений нужно рассмотреть другую целевую функцию . После того, как задача на максимум будет решена и будет найден оптимальный опорный план , можно будет воспользоваться равенством: .

1.4. Двойственность в линейном программировании

Пусть задана общая задачи линейного программирования

(1.15)

Тогда задачей, двойственной к задаче (1.15) называется следующая задача:

(1.16)

Двойственная задача строится следующим образом:

1. каждой переменной основной задачи ставится в соответствие ограничение двойственной задачи и, наоборот, каждому ограничению основной задачи ставится в соответствие переменная двойственной задачи. Таким образом, двойственная задача содержит n ограничений и m переменных .

2. Если исходная задача (1.15) является задачей на максимум с ограничениями, являющимися равенствами, или неравенствами вида «£». Тогда двойственная задача (1.16) является задачей на минимум с ограничениями, являющимися равенствами, или неравенствами вида «³».

3. Коэффициенты целевой функции двойственной задачи (1.16) совпадают с правыми частями системы ограничений исходной задачи (1.15).

4. Правые части системы ограничений двойственной задачи (1.16) совпадают с коэффициентами функции цели исходной задачи (1.15).

5. Матрица системы ограничений задачи (1.16) является транспонированной матрицей системы ограничений задачи (1.15).

6. Те ограничения двойственной задачи (1.16), которые соответствуют ограниченным на знак переменным исходной задачи (1.15), имеют вид неравенств вида «³». Остальные ограничения двойственной задачи являются равенствами.

7. Те переменные двойственной задачи (1.16), которые соответствуют ограничениям исходной задачи вида «£», ограничены на знак. Остальные переменные двойственной задачи ограничений на знак не имеют.

Основные теоремы двойственности:

Теорема 1.1. Задача, двойственная к двойственной задаче (1.16) совпадает с исходной задачей (1.15).

Теорема 1.2. Пусть – произвольный план задачи (1.15), – произвольный план задачи (1.16), тогда имеет место неравенство .

Теорема 1.3. Если и - оптимальные планы задач (1.15) и (1.16), соответственно, то имеет место равенство .

Теорема 1.4. Если одна из задач (1.15) и (1.16) не имеет решения из-за неограниченности целевой функции, то другая не имеет решения из-за отсутствия планов. И наоборот.

Теорема 1.5 («о равновесии»). Если при подстановке оптимального опорного плана в систему ограничений одной из взаимно-двойственных задач какое-то ограничение обращается в строгое неравенство, то соответствующая компонента оптимального опорного плана другой задачи равна нулю.Еслиже некоторая компонента оптимального опорного плана одной из взаимно-двойственных задач строго больше нуля, то при подстановке оптимального опорного плана другой задачи в свою систему ограничений соответствующее ограничение будет обращаться в строгое равенство.

В качестве примера использования теорем двойственности решим задачу, двойственную к задаче (1.12) – (1.13).

Пример 1.2. Требуется решить задачу, двойственную к задаче

(1.17)

Решение. Умножим второе ограничение задачи (1.17) на –1для того, чтобы оно имело вид неравенства вида « »:

(1.18)

Составим задачу, двойственную к задаче (1.18):

(1.19)

Обозначим через – искомый оптимальный опорный план двойственной задачи (1.19). Для его поиска воспользуемся теоремой о равновесии. Сначала подставим координаты оптимального опорного плана в систему ограничений задачи (1.18):

Так как первое ограничение превратилось в строгое неравенство, то соответствующая компонента оптимального опорного плана двойственной задачи равна нулю (). Осталось найти компоненты и . Для этого воспользуемся второй частью теоремы о равновесии.

1. Так как вторая и третья компоненты оптимального опорного плана строго больше нуля, то соответствующие ограничения двойственной задачи, при подстановке в них компонент оптимального плана , обратится в равенства. Данные равенства дают нам систему линейных уравнений для нахождения и :

(1.20)

Решая систему (1.20), с учетом того, что , получим оптимальный опорный план двойственной задачи (1.19): 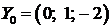. При этом выполняется теорема 1.3: .

Глава 2. АЛГОРИТМЫРЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО
ПАРАМЕТРИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Многие прикладные задачи сводятся к решению задач параметрического программирования. Дело в том, что коэффициенты целевой функции, а также правые части и коэффициенты системы ограничений задачи линейного программирования могут изменяться в зависимости от внейшних условий, в которых решается задача.

Так, например, если решается задача управления производством, то коэффициенты целевой функции совпадают с ценой на единицу продукции того или иного вида выпускаемой продукции. Они могут зависеть от курса доллара, нефтяных котировок, времени хранения продукции, времени года и т.д. Правые части системы ограничений (запасы сырья) могут зависеть от своевременности поставок, времени года, наличия средств на их приобретения. Технологические коэффициенты (коэффициенты системы ограничений) могут зависеть от тех или иных технологических требований.

Наиболее простыми задачами параметрического программирования, содержащими параметры, являются задачи, содержащие один параметр, линейно входящий в соответствующие коэффициенты.

При каждом значении параметра задача является обычной задачей линейного программирования. Однако каждый раз решать задачу, как только изменяется хотя бы один входящий в нее параметр, представляется крайне нерациональным. Это связано с тем, что многие задачи содержат большое количество переменных и требуют определенного времени на их решение.

Рассмотрим наиболее распространенные задачи параметрического программирования.

2.1. Алгоритм решения задачи параметрического программирования
с переменными коэффициентами целевой функции

Рассмотрим следующую задачу линейного программирования

, (2.1)

(2.2)

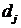В целевой функции числа и известны и постоянны, а величина является переменным параметром.

В данном случае найти оптимальный план непросто, так как он может оказаться не единственным при разных значениях t. При изменении параметра t градиент целевой функции (2.1) непрерывно меняет свое направление, а многогранник, состоящий из решений системы (2.2) остается неизменным. Поэтому вопрос задачи ставится следующим образом.Требуется разбить отрезок 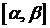на конечное число интервалов, на каждом из которых действует один и тод же оптимальный опорный план.

Алгоритм решения этой задачи состоит из двух действий:

Находим оптимальный опорный план, соответствующий случаю, когда 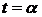. (Левый конец интервала ).

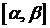1) Определяем все значения параметра t, для которых максимум достигается в той вершине. Найденный интервал исключаем из заданного отрезка 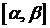. Для оставшегося интервала снова решаем задачу, т. е. переходим к п.1 алгоритма. Так продолжаем до тех пор, пока не будет разделен на частичные интервалы весь отрезок .

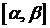Рассмотрим алгоритм подробно

1) Полагаем 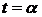. Тогда целевая функция принимает вид

(2.3)

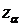Составляем жорданову таблицу, в которую добавляем две строки: для коэффициентов и (табл. 2.1). В строке этой таблицы в каждом столбце фактически будет стоять не два числа и , а одно число, равное их сумме. В последних двух строках таблицы записана линейная форма для произвольного параметра . Для получения надо умножить на коэффициенты последней строки и сложить их с коэффициентами предпоследней.

Табл. 2.1

	-x₁	-x₂	…	-x_n
y₁= y₂= … y_m=	(a_ij)	a₁ a₂ a_m
z_a=	c₁+d₁a c₂+d₂a … c_n+d_na
	c₁ d₁	c₂ d₂		c_n d_n

Решаем записанную в таблице задачу, т. е. обычным симплекс-методом находим оптимальныйопорный план. При этом всем преобразованиям подвергаем и коэффициенты последних двух строк. Новые коэффициенты обозначим через и ; здесь же появятся свободные члены и .

Преобразованная таблица будет иметь вид:

Табл. 2.2

…

Поделиться:

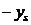
Поиск по сайту

©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2018-01-31 Нарушение авторских прав и Нарушение персональных данных

Поиск по сайту:

Читайте также:

Деталирование сборочного чертежа

Когда производственнику особенно важно наличие гибких производственных мощностей?

Собственные движения и пространственные скорости звезд

Тема 11. Банковские риски и способы их оценки

Опросник «Активность повседневной жизни»

Интересно:

Как защитить исследовательскую работу (проект)

Что такое ХЭШТЕГ и как им пользоваться в сети

Какие несчастные случаи на производстве подлежат расследованию и учету?

Как устроена магнитная головка

Обратная связь