Определение теплоемкости металлов

Лабораторные работы

По курсу общей физики

²Строение вещества²

Утверждено редакционно- издательским советом института

 

 

Москва 2007

 

 

УДК 537(076.5)

Рецензент докт. физ.-мат. наук, проф. С.В. Селищев

Берестов А.Т., Боргардт Н.И., Куклин С.Ю.

Лабораторные работы по курсу общей физики ²Строение вещества²/ М.: МИЭТ, 2007. - 50 с.: ил.

Пособие содержит описания лабораторных работ по курсу общей физики ²Строение вещества². Описания работ включают краткое изложение сущности изучаемых явлений, сведения о методике, приемах проведения измерений и обработки экспериментальных результатов.

Предназначено для студентов 2-го курса технических факультетов МИЭТ.

 

ã МИЭТ, 2007

Предисловие

Данное пособие содержит описания 7 лабораторных работ по курсу общей физики ²Строение вещества², изучаемого студентами второго курса технических факультетов МИЭТ. Работы посвящены изучению элементов квантовой механики и физики твердого тела. В курсах лабораторных работ ²Механика², ²Электричество и магнетизм², ²Оптика² изучались законы классической физики, сформулированные к концу ХIХ столетия. Отличие данного курса лабораторных работ состоит в том, что законы, обсуждаемые и проверяемые в нем, сформулированы в ХХ столетии и являются основой современной электроники. Можно сказать, что этот курс является связующим звеном между курсом общей физики и спецкурсами, которые будут изучаться студентами технических факультетов на других кафедрах.

Представленные в пособии лабораторные работы являются развитием практикума, который существует на кафедре общей физики с середины 70-х годов, в становление которого следует отметить большой вклад Музюкина Л.П..

Модернизация и обновление лабораторных работ, введение в практикум новых работ, выполненные в последние годы под руководством Берестова А.Т. и Кривошеева В.И., потребовали существенного переработки и дополнения описаний лабораторных работ. Большую техническую помощь в настройке лабораторных установок, введении их в учебный процесс и в подготовке новых описаний оказали инженеры кафедры общей физики Королева Е.Н., Кривошеев В.И., Смелова Е.А.

Авторы выражают благодарность преподавателям кафедры общей физики Гайдукову Г.Н., Фаттахдинову А.У., Лосеву В.В. и др. за полезные замечания и советы, сделанные в процессе подготовки рукописи.

Каждое описание включает краткое изложение сущности изучаемых явлений, сведения об экспериментальной методике, описание приемов проведения измерений и обработки результатов. Лабораторные работы рассчитаны на четырехчасовые занятия и состоят из нескольких упражнений.

Обработку результатов измерений необходимо проводить сразу после их получения, т.е. в лаборатории, но никак не дома. Как правило, при обработке результатов возникает необходимость что-то уточнить, проверить, дополнительно измерить, Поэтому можно считать обязательным условием последовательную обработку результатов измерений.

При оформлении лабораторных работ следует соблюдать следующее:

1) заголовок должен быть выделен;

2) рисунки и графики следует оформлять в карандаше, графики – на ²миллиметровке², причем их необходимо вклеивать в лабораторный журнал;

3) результаты измерений и расчетов целесообразно свести в таблицу;

4) все результаты приводятся с указанием погрешности.

 

Лабораторная работа № 1

 

Тепловое излучение

 

Цель работы:исследование теплового излучения вольфрамовой нити лампы нака­ливания, оз­на­комление с работой пирометра с исчезающей нитью и проверка справедли­вости закона Стефана-Больц­мана.

 

Теоретическая часть

 

Излучение электромагнитной энергии веществом за счет его внутренней энергии называется тепловым излучением. Свойства теплового излучения определяются материалом тела и его температурой Т. Если из любого материала сделать замкнутую по­лость и под­держивать температуру ее стенок постоянной, то система (стенка + излучение) придет в состояние тер­модинамического равновесия, и в объеме полости установится рав­новесное тепловое излучение.

По­ток энергии, испускаемый единицей поверхности излучающего тела за единицу времени по всем на­правлениям (в пределах телесного угла 2p), называ­ется энергетиче­ской светимостью тела R. Излу­чение состоит из волн различных частот w (или длин волн l). При малой величине интервала частот d w поток энергии, излучаемый единицей по­верхности в интервале частот d w, пропорционален d w:

dR _w = r _w d w

Величина r _w называется испускательной (излучательной) способностью тела. Зная r _w, можно оп­ределить энергетическую светимость тела:

.

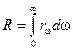Пусть на элементарную площадку поверхности тела падает поток энергии 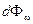, обусловлен­ный электромагнитными волнами, частота которых заключена в интер­вале частот от w до w + d w. Часть потока 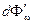будет поглощена телом. Безразмерная вели­чина

называется поглощательной способностью тела. Она зависит от температуры тела Т. Тело, для которого для всех частот, называют абсолютно черным. Если а _{w Т} = const < 1, то тело называют серым.

Кирхгоф сформулировал следующий закон: отношение испускательной и поглоща­тель­ной спо­собностей не зависит от природы тела, оно является для всех тел одной и той же универсальной функ­цией частоты и температуры:

Функция называется функцией Кирхгофа, она по сути представляет собой испускатель­ную способность абсолютно черного тела.

Стефан и Больцман, исходя из экспериментальных данных и термодинамических сооб­ражений, установили, что энергетическая светимость абсолютно черного тела R ^* про­порциональна четвертой степени температуры (закон Стефана-Больцмана):

,

где s = 5,67×10^-8 Вт×м^-2 ×К^-4 - постоянная Стефана-Больц­мана.

Планк, сделав предположение, что электромагнитное излучение испускается в виде от­дельных порций энергии e (квантов), величина которых пропорциональна частоте излуче­ния, установил вид функции Кирхгофа (формула Планка):

,

где = 1,05×10^-34 Дж×с - постоянная Планка; = 1,38×10^-23 Дж/К - постоянная Больцмана; = 3×10⁸ м/с -скорость света в вакууме.

Зная функцию и поглощательную способность тела a _{w T}, можно определить энергетическую светимость тела

.

Температурная зависимость R (Т) реального тела отличается от зависимости R ^*(Т) для абсолютно черного тела, однако общий вид обычно сохраняется:

R~Tⁿ,

где n близко к четырем.

 

Экспериментальная часть

 

В данной работе наблюдается излучение вольфрамовой нити лампы накаливания. Для вольфрама согласно закону Кирхгофа

,

поэтому

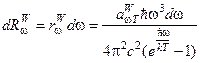. (1)

Измерение температуры излучающих тел осуществляется с помощью пирометров – приборов для измерения температуры бесконтактным методом по интенсивности их те­плового излучения. Пирометры подразделяются на три основные группы: радиационные, яркостные и цветовые.

В данной работе используется яркостный пирометр с исчезающей нитью, сравни­вающий излучение вольфрамовой нити лампы накаливания с из­лучением абсолютно черного тела на одном и том же фиксиро­ванном узком участке спектра от w до w + Dw. Наблюдая в окуляр совмещен­ные в одной плоскости изображения светящейся спирали и нити накала пирометра (см рис.), с помощью реостата подбира­ется такой накал нити пирометра, чтобы ее яркость совпала с яр­костью изображения спирали. В этом случае нить «исчезает», т.е. становится неразличимой на фоне изображения спирали. Прибор проградуирован так, что показывает значение температуры Т ^* абсолютно черного тела, излучающего на длине волны l = 660 нм так же, как излучает исследуемая спираль в дан­ных условиях.

Для определения температуры Т спирали необходимо сделать пересчет. Для абсо­лютно черного тела

. (2)

При одинаковой яркости спирали лампы и нити пирометра будут одинаковыми и энерге­тические светимости в заданном интервале частот. Используя условие (объясните, почему оно выполняется) и, приравнивая энергетиче­ские светимо­сти (1) и (2), получаем

, (3)

где - яркостная температура (температура, определяемая с помощью нити пирометра, прокалиброван­ной по излучению абсолютно черного тела); 1,438×10^-2 (м×К); l = 660 нм - длина свето­вой волны (средняя длина волны, пропускаемая светофильтром); - температура вольфрама; = 0,43 - поглощательная способность вольф­рама в исследуе­мом диапазоне температур.

Выполнение работы

 

Изменение яркости свечения лампы накаливания осуществляется регулировкой на­пря­жения пи­тания с помощью ручки регулировки на стенде (рис.1). Напряжение нити и ток через нее измеряется вольт­метром и амперметром. Это позволяет подсчитать подводимую мощ­ность .

Рис 1. Передняя панель установки

 

Яркость свечения нити пирометра регулируется вращением кольца-движка потен­цио­метра, расположенного под окуляром прибора. Сила тока измеряется ампермет­ром пирометра, шкала которого проградуирована в градусах Цельсия. Имеется два диапазона измене­ния температуры: 700 -1400 °C и 1200 - 2000 °С. Для перехода на второй диапазон на пути света от лампы накаливания ставится светофильтр (нажатием и поворотом кнопки, расположенной за шкалой амперметра). С помощью двух выдвижных тубусов (со стороны окуляра и объектива пирометра) обеспечива­ется фокусировка изображения ни­тей.

При достаточно высокой температуре практически вся подводимая мощность рас­сеивается через излучение и пропорциональна энергетической светимости R ~ Tⁿ спи­рали. Поэтому

Р = ВТⁿ,

где В – константа.

Отсюда следует, что

ln P = n ln T + ln B.

Это уравнение прямой в логарифмических координатах.

По результатам измерений постройте график зависимости ln P от 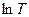и найдите вели­чину n как угловой коэффициент этого графика. Оцените погрешность полученной величины.

 

Литература

 

1. Савельев И.В. Курс общей физики. - М.: Астрель, АСТ. 2003 – кн.5, Гл. 1

2. Сивухин Д.В. Общий курс физики. Оптика. - М.: ФИЗМАТЛИТ МФТИ 2002 - Гл. X.

 

Лабораторная работа № 2

 

Определение теплоемкости металлов

Цель работы:экспериментальное определение теплоемкости металла, сравнение с законом Дюлонга и Пти.

Теоретическая часть

Теплоемкостью тела называется величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один градус:

.

Удельной теплоемкостью вещества называется теплоемкость единицы массы ве­щества:

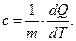
Молярной теплоемкостью вещества называется теплоемкость массы вещества, равной молярной массе этого вещества:

, (1)

где m /m - количество молей вещества.

Величина теплоемкости зависит от условий нагревания. Процесс нагревания вещества при постоянном объеме характеризуется "теплоемкостью при постоянном объеме" с _v, а при постоянном давлении – "теплоемкостью при постоянном давлении" с_{р .} Для этих теплоемкостей всегда справедливо соотношение с_p > c _v – это доказывается с помощью термодинамических законов. Например, для идеального одноатомного газа молярные теплоемкости c _v = , а с_р = .

Для твердых тел различие между этими теплоемкостями пренебрежимо мало, так как объем твердых тел при нагревании меняется мало ( при изменении температуры на 1 К). Поэтому говорят просто о теплоемкости твердого тела.

Из теории теплоемкости твердых тел, разработанной Эйнштейном и Дебаем, вытекают следующие важные положения, касающиеся поведения теплоемкости при низких и высоких температурах:

а) при стремлении абсолютной температуры к нулю теплоемкость тела также стремится к нулю

,

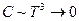б) при температурах, существенно превышающих значение так называемой характеристической температуры Дебая Т _Д, молярная теплоемкость химически простых тел в кристаллическом состоянии есть величина постоянная, и равная

с _m = 3 R,

где R = 8,31 Дж/(моль×К) – универсальная газовая постоянная.

Последнее утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем и подтверждаемого классической статистической физикой. Действительно, из закона равномерного распределения энергии по степеням свободы следует, что на каждую степень свободы приходится энергии kT /2 ( - постоянная Больцмана). В кристаллическом состоянии атомы совершают малые колебания вблизи положения равновесия. На каждую колебательную степень свободы приходится энергия kT, равная сумме средних значений кинетической и потенциальной энергий. Число колебательных степеней свободы из кристалла, содержащего N атомов, равно 3 N. Поэтому средняя энергия теплового движения в кристалле равна . Соответствующая молярная теплоемкость равна

,

здесь N_А = 6,02×10²³ моль^-1 – постоянная Авогадро.

Теплоемкость кристаллов оказывается не зависящей от температуры и от конкретных свойств кристаллов.

Характеристические температуры Дебая некоторых кристаллов приведены в таблице 1.

Таблица 1

Кри­сталл	Pb	J	Na	Ag	NaCl	Cu	Al	Fe	Cr	Be	C (алмаз)
Т Д, К

 

Из приведенной таблицы характеристических температур следует, что для кристал­лов от свинца (Pb) и до поваренной соли (NaCl) комнатная температура (~ 300К) и бо­лее высокие темпе­ратуры являются сравнительно большими. Поэтому для подобных кристаллов отклоне­ния от закона Дюлонга и Пти в этой области температур не велики. Но, например, для бериллия и алмаза поведение теплоемкости при умеренных температурах совершенно отличается от закона Дюлонга и Пти. На рис.1 показана температурная зависимость теплоемкости кристалла меди.

 

Рис.1 Температурная зависимость теплоемкости меди

 

Экспериментальная часть

 

В работе производится измерение теплоемкости медного или алюминиевого образцов, имеющих цилиндрическую форму. На их боковую поверхность для обеспечения теплового контакта плотно намотан константановый провод, являющийся нагревателем, и медный провод, который выполняет функцию термометра на основе зависимости его сопротивления от температуры. Образец устанавливается на трех тонких стойках внутри теплоизолирующей оболочки, изготовленной из пенопласта. Стойки сделаны из нержавеющей стали, имеющей низкий коэффициент теплопроводности.

Теплоизолирующая оболочка вместе с образцом представляют собой измерительную ячейку. Она с помощью разъема подключается к измерительному блоку, содержащему источники стабильного тока питания нагревателя и термометра, сопротивления в цепи нагревателя и термометра , измерительные приборы – электронные вольтметр, милливольтметр, а также секундомер. Электрическая схема установки для измерения теплоемкости показана на рис.2.

Рис.2 Электрическая схема установки для измерения теплоемкости

 

При выполнении эксперимента необходимо определить количество тепла , подведенного к образцу за время t, и возникающую при этом разность температур D Т. Величина находится на основе закона Джоуля-Ленца

. (2)

Напряжение измеряется вольтметром, - милливольтметром при подключении его к сопротивлению (положение 1 переключателя), время t определяется по разности показаний секундомера при включении и выключении нагрева.

Температура рассчитывается исходя из температурной зависимости сопротивления медного провода термометра. В диапазоне исследуемых температур для меди с погрешностью не хуже 0,1% можно воспользоваться линейной зависимостью

,

где R ₀ - сопротивление термометра при t = 0 ^оC, а температурный коэффициент сопротивления меди a = 0,0043 К^-1.

Величина R _т рассчитывается по закону Ома

.

Напряжение U _тт определяется по показаниям милливольтметра в положении 2 переключателя, U _т- в положении 3 этого переключателя.

Используя выражение для , температуру образца можно вычислить по формуле

. (3)

Для определения возникающей при нагреве разности температур D Т используется метод термограмм (или температурных ходов). Суть его состоит в том, что на протяжении отрезка времени через определенные временные интервалы измеряется температура образца. Это делается до нагрева, в течение нагрева и после него. При этом возникает зависимость, схематически представленная на рис.3.

Рис.3 Изменение температуры образца в процессе измерений

 

Участок 0 - 1 по времени соответствует температурному ходу до нагрева. Он или горизонтальный, если образец перед измерениями находился при комнатной температуре, или наклонный (падающий), если образец был нагрет, например, при проведении предыдущего эксперимента. Участок 1 - 2 соответствует нагреву при постоянной подводимой мощности, участок 2 - 3 – охлаждению образца после выключения нагрева. Вследствие малого теплообмена и практически постоянной теплоемкости образца в диапазоне исследуемых температур эти ходы с хорошей точностью являются линейными. Как показывают расчеты, основанные на решении уравнений теплопроводности и теплообмена, экстраполяция ходов 0 - 1 и 2 - 3 к середине промежутка времени нагрева позволяет определить величину Δ Т изменения температуры образца при его нагреве.

После определения количества подведенного тепла и возникающей при нагреве разности температур молярная теплоемкость находится как

(4)

Масса образца вычисляется по формуле

,

где r - плотность материала образца, а его размеры равны: диаметр D = 5,0 см, высота H = 5,0 см.

Выполнение работы

 

Перед выполнением работы внимательно изучите с экспериментальную установку, состоящую из измерительной ячейки и измерительного блока. На передней панели измерительного блока (рис.4) расположены цифровые вольтметр, милливольтметр и секундомер, тумблеры «Сеть», «Время» и «Нагрев», переключатель «Режим измерений», кнопка «Сброс», устанавливающая нулевое значение на секундомере.

 

Рис.4 Передняя панель измерительного блока

 

До проведения измерений внесите в конспект значения сопротивлений и в цепях нагревателя и термометра соответственно, сопротивление термометра при t = 0 °C, которые приведены на рабочем месте для каждой установки. Для записи результатов измерений подготовьте следующую таблицу.

Таблица 2

№№	Время, с	U т, мВ (переключатель в положении 3)	U тт, мВ (переключатель в положении 2)	U нт, мВ (переключатель в положении 1)	U н, В
и т.д.

 

Перед включением установки (тумблер «Сеть») необходимо установить в положение «Выкл» тумблеры «Нагрев» и «Время». После включения установки показание вольтметра и секундомера должны быть нулевыми. Устанавливая переключатель «Режим измерений» в положения 3 и 2 измерьте U _т и U _тт и заносите их в таблицу. Затем включается секундомер и измерения U _т и U _тт повторяются с интервалом 100 с. Для повышения достоверности снимаемых данных при подходе к очередной временной отметке в первую очередь измеряют напряжение на термометре, поскольку именно этой величина определяется изменение температуры. Хотя токи I _т и I _н задаются источниками стабильного тока, их значения, а также напряжение U _н необходимо контролировать в процессе проведения эксперимента.

Проведя измерения для 15 ÷ 20 временных отметок, определяющих начальный температурный ход, в момент времени, который соответствует последней из них и должен быть записан в конспект, с помощью тумблера «Нагрев» включается питание нагревателя. На вольтметре высвечивается показания, соответствующие U _н. Нагрев рекомендуется проводить в течение 600 - 800 с, т.е. снять при нагревании 6 ÷ 8 точек, выполняя необходимые измерения. После этого нагрев выключается в момент времени, соответствующий одной из временных меток, которую также следует записать. Далее следует продолжить измерения величин, определяющих температурных ход после нагрева, снимая показания приборов для 15 ÷ 20 точек с интервалом 100 с.

В процессе обработки результатов эксперимента для каждой временной отметки рассчитывается температура образца по измеренным значениям U _т, U _тт, известным величинам R _тт и R ₀ (формула (3)) и строится график зависимости температуры от времени. Разность температур Δ Т, как говорилось выше, определяется путем линейной экстраполяции температурных ходов до и после нагрева к моменту времени, соответствующему середине нагрева. Количества переданного образцу тепла находится по формуле (2), используя измеренные значения U _н, U _нт, известное значение сопротивления R _нт и время нагрева τ. На основе вычисленных и Δ Т рассчитывается молярная теплоемкость образца по формуле (4).

Для упрощения процедуры нахождения и повышения точности вычислений в работе предусмотрена компьютерная обработка данных. При обращении к соответствующей программе на экране монитора высвечивается таблица, аналогичная таблице 2, а также ячейки, в которые заносятся параметры установки. После ввода результатов измерений методом наименьших квадратов осуществляется линейная интерполяция температурных ходов до и после нагрева, расчет Δ Т и молярной теплоемкости образца с _m, которая сравнивается с величиной 3 R, соответствующей закону Дюлонга и Пти.

Справочные данные

Материал	Cu	Al
Плотность r, г/см3	8,960	2,699
Молярная (атомарная) масса m, г/моль	63,55	26,98

Литература

1. Савельев И.В. Курс общей физики. - М.: Астрель, АСТ. 2003 – кн.3, § 4.5

 

Лабораторная работа № 3