Цель работы:исследование термоэлектронной эмиссии с поверхности катода вакуумного диода и определение работы выхода материала катода.
Теоретическая часть
Термоэлектронная эмиссия – явление испускания электронов с поверхности нагретого металла. Для получения заметной величины термоэлектронной эмиссии необходимо нагреть металл до температуры, значительно выше комнатной (2000-2500 К).
Металл представляет собой кристаллическое тело, в узлах решетки которого расположены положительно заряженные ионы, между которыми свободно перемещаются электроны, оторвавшиеся от атомов (свободные электроны). Вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Они возникают вследствие притяжения между электронами и положительными ионами решетки. Таким образом, для того чтобы электроны могли покинуть поверхность металла, им необходимо сообщить некоторую дополнительную энергию.
Вследствие квантовых эффектов энергия электронов внутри металла может принимать только дискретные значения, причем обладать одинаковой энергией с учетом спина электрона могут не более двух электронов. Энергетическая диаграмма электронов в металле (в потенциальной яме) при температуре Т = 0 К изображена на рис.1. Сплошными линиями изображены энергетические уровни, занятые электронами (на каждом уровне - два электрона), а пунктирными линиями - свободные уровни. Энергия последнего уровня, занятого электронами, называется уровнем Ферми или энергией Ферми ЕF.

Рис.1. Энергетическая диаграмма электронов в металле при абсолютном нуле, 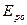 - энергия, соответствующая дну потенциальной ямы (зоны проводимости),
- энергия, соответствующая дну потенциальной ямы (зоны проводимости), 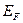 - энергия Ферми
- энергия Ферми
Для удаления электрона за пределы металла разным электронам нужно сообщить, очевидно, неодинаковую энергию. Наименьшая энергия, необходимая электрону для того, чтобы покинуть поверхность металла в вакууме называется работой выхода А электрона из металла. Ее часто обозначают как е j, где  = 1,6×10-19 Кл - элементарный заряд, j - так называемый потенциал выхода.
= 1,6×10-19 Кл - элементарный заряд, j - так называемый потенциал выхода.
Из диаграммы следует, что в соответствии с определением работы выхода ее величина при Т = 0 К
 .
.
Определение работы выхода распространяется и на температуры, отличные от абсолютного нуля. При этом следует учесть, что энергия Ферми и глубина потенциальной ямы зависят от температуры. Это приводит к тому, что работа выхода также зависит от температуры. Но эта зависимость слабая. В данной работе мы пренебрегаем зависимостью работы выхода от температуры.
Распределение электронов в металлах подчиняется распределению Ферми-Дирака, согласно которому вероятность того, что состояние с энергией  при температуре Т занято электроном, равна
при температуре Т занято электроном, равна

где  - постоянная Больцмана,
- постоянная Больцмана,  - абсолютная температура. Вид этого распределения показан на рис.2.
- абсолютная температура. Вид этого распределения показан на рис.2.

Рис. 2. Распределение электронов в металле по энергиям для температур  и
и 
При низких температурах количество электронов, обладающих энергией, достаточной для выхода из металла, незначительно. При повышении температуры доля электронов, имеющих энергию, превышающую энергию Ферми, увеличивается. К тому же максимальная энергия таких электронов также увеличивается (см. рис.2). Она может стать настолько большой, что некоторые из электронов могут преодолеть энергетический барьер и выйти наружу. Если в окружающем вакууме существует электрическое поле, направленное к поверхности металла, то оно будет увлекать вышедшие электроны, и через вакуум потечет термоэлектронный ток.
Для наблюдения термоэлектронной эмиссии удобна вакуумная лампа с двумя электродами - вакуумный диод. Такие лампы применяются в радиотехнике для выпрямления переменного тока.
Катодом лампы служит проволока (нить) из тугоплавкого металла (вольфрам, молибден и др.), накаливаемая электрическим током. Получить сильные термоэлектронные токи с катодами из этих металлов можно лишь при очень высоких температурах накала, т.к. работа выхода из тугоплавких металлов относительно велика (А = 4,52 эВ для вольфрама). Между тем на практике весьма существенно снизить рабочую температуру катода для уменьшения затрат энергии и увеличения срока службы лампы. Это достигается созданием на поверхности катода тонкого покрытия ионами щелочноземельных металлов (толщиной в несколько атомных слоев). Покрытие сильно понижает работу выхода и тем самым увеличивает эмиссионную способность катода.
Экспериментальная часть
Исследование термоэлектронной эмиссии осуществляется с помощью вакуумного диода, схематическое устройство которого показано на рис.3. Проволока К из вольфрама с покрытием (катод) окружена цилиндрическим анодом А и помещена в вакуумный баллон Б.
 |
Рис. 3. Схематическое устройство вакуумного диода. К - катод, А - анод, Б - вакуумный баллон
Катод нагревается до требуемой температуры током накала. Если, поддерживая температуру накаленного катода постоянной, менять напряжение Ua между анодом и катодом, то термоэлектронный ток Ia сначала будет возрастать. Однако это возрастание идет не пропорционально Ua, т.е. для вакуумного диода закон Ома не выполняется. При достижении определенного напряжения дальнейшее нарастание термоэлектронного тока практически прекращается и ток достигает предельного значения I нас, называемого током насыщения. Зависимость анодного тока  от анодного напряжения Ua для ряда температур (вольт-амперная характеристика) показана на рис.4.
от анодного напряжения Ua для ряда температур (вольт-амперная характеристика) показана на рис.4.
Наличие тока насыщения имеет следующее объяснение. Его величина определяется количеством электронов, которое покидает поверхность катода в единицу времени (т.е. температурой катода). Если электрическое поле между анодом и катодом способно отвести все электроны, испускаемые катодом, то дальнейшее увеличение анодного напряжения Ua уже не может привести к увеличению термоэлектронного тока.
 |
Рис. 4. Вольт-амперные характеристики вакуумного диода. Температуры катода 
При малых напряжениях между катодом и анодом ток практически не зависит от температуры катода и подчиняется так называемому закону трёх вторых, т. е. в этом случае  (криволинейный пунктир на рис.4). При дальнейшем увеличении напряжения ток насыщения растет очень незначительно. Зависимость тока насыщения
(криволинейный пунктир на рис.4). При дальнейшем увеличении напряжения ток насыщения растет очень незначительно. Зависимость тока насыщения  от температуры и работы выхода определяется формулой Ричардсона-Дэшмана:
от температуры и работы выхода определяется формулой Ричардсона-Дэшмана:
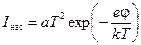 , где
, где  = 1,38×10-23 Дж/К - постоянная Больцмана, а - некоторая константа, зависящая от свойств конкретного металла.
= 1,38×10-23 Дж/К - постоянная Больцмана, а - некоторая константа, зависящая от свойств конкретного металла.
Прологарифмировав последнее равенство, получим
 .
.
Таким образом, зависимость  от
от  линейная. Угловой коэффициент прямой
линейная. Угловой коэффициент прямой  позволяет определить работу выхода А = е j из экспериментальных вольт-амперных характеристик вакуумного диода, что является целью данной работы.
позволяет определить работу выхода А = е j из экспериментальных вольт-амперных характеристик вакуумного диода, что является целью данной работы.
Температуру катода можно определить, воспользовавшись зависимостью сопротивления катода 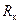 от температуры. В исследуемом диапазоне температур эту зависимость с достаточной точностью можно считать линейной:
от температуры. В исследуемом диапазоне температур эту зависимость с достаточной точностью можно считать линейной:
 . (1)
. (1)
Здесь t - температура в °С,  - сопротивление катода при t = 0 °С, a - температурный коэффициент сопротивления материала катода. По закону Ома сопротивление катода
- сопротивление катода при t = 0 °С, a - температурный коэффициент сопротивления материала катода. По закону Ома сопротивление катода
 , (2)
, (2)
где 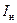 - ток накала,
- ток накала,  - напряжение накала. Из (1) и (2) легко определить абсолютную температуру катода:
- напряжение накала. Из (1) и (2) легко определить абсолютную температуру катода:
 (3)
(3)
Выполнение работы
На рис.5 представлена электрическая схема экспериментальной установки.
 |
Рис. 5. Электрическая схема установки
Конструктивно установка выполнена в виде единого блока, внешний вид которого приведен на рис.6.

Рис 6. Передняя панель установки
На панели расположены: электронная лампа, вольтметры и амперметры анодной и катодной цепей, тумблер «сеть», ручки регулировки источников анодного и катодного напряжений. Источники напряжения размещены внутри блока вместе с соединительными проводами.
Внимательно ознакомьтесь с установкой. Перед включением рекомендуется установить ручки регулировки анодного и катодного напряжений в нулевое положение, повернув их против часовой стрелки.
Включив установку, снимите и нанесите на миллиметровой бумаге несколько (не менее трех) вольтамперных характеристик диода Ia (Ua)при различных токах накала I н.
Для каждой из характеристик определите значения  ,
, 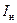 и
и  , а затем и сопротивление катода
, а затем и сопротивление катода 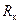 по соотношению (2).
по соотношению (2).
По уравнению (3) рассчитайте температуру катода для каждого тока накала.
Постройте на миллиметровой бумаге график зависимости  от
от  и по угловому коэффициенту определите работу выхода А = e j в эВ.
и по угловому коэффициенту определите работу выхода А = e j в эВ.
Оцените погрешность полученной величины работы выхода.
Данные для расчета: 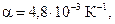 R 0 = 0,25 Ом, 1 эВ = 1,6×10-19 Дж
R 0 = 0,25 Ом, 1 эВ = 1,6×10-19 Дж
Литература
1. Калашников С.Г. "Электричество". - М.: ФИЗМАТЛИТ, 2003, §§ 156-158
2. Сивухин Д. В. Общий курс физики. Электричество. - М.: ФИЗМАТЛИТ, 2002,
§ 101
Лабораторная работа № 4
Эффект Холла в полупроводниках
Цель работы: изучение эффекта Холла, определение проводимости полупроводника, постоянной Холла, концентрации и подвижности носителей заряда в полупроводнике.
Теоретическая часть
На точечный заряд q, движущийся со скоростью  в магнитном поле c индукцией
в магнитном поле c индукцией  , действует сила Лоренца
, действует сила Лоренца  . Эта сила, перпендикулярная и скорости движения заряда, и направлению магнитного поля приводит к эффекту Холла, который можно наблюдать в металлах и полупроводниках.
. Эта сила, перпендикулярная и скорости движения заряда, и направлению магнитного поля приводит к эффекту Холла, который можно наблюдать в металлах и полупроводниках.
Суть эффекта Холла рассмотрим на следующем примере:
Образец в виде прямоугольной пластинки полупроводника поместим в магнитное поле (рис.1,а), направленное от нас, и пропустим через образец электрический ток плотностью j слева направо.


а) б)
Рис 1. Образец для измерения холловского напряжения
В полупроводнике носителями заряда являются отрицательно заряженные электроны и положительно заряженные дырки. Сила Лоренца, действующая на них, имеет одинаковое направление, несмотря на то, что электроны и дырки движутся в противоположных направлениях (объяснит, почему). Если концентрация носителей одного типа преобладает (примесный полупроводник n - или р- типа), то верхняя и нижняя грани пластинки будут заряжены зарядами противоположного знака. (Определите, какого типа полупроводник изображен на рис.1,а). При этом возникает противоположное по отношению к  электрическое поле
электрическое поле  (рис.1,б). Это поле называется полем Холла, а явление возникновения поперечного электрического поля под действием магнитного поля называется эффектом Холла.
(рис.1,б). Это поле называется полем Холла, а явление возникновения поперечного электрического поля под действием магнитного поля называется эффектом Холла.
Если наряду с магнитным существует и электрическое поле, то сила Лоренца приобретает вид:
 .
.
При отсутствии тока в поперечном направлении проекция силы Лоренца на это направление равна нулю:  . В результате
. В результате
Ех = VB. (1)
Это выражение будет использовано для определения разности потенциалов Холла.
Рассмотрим некоторые вопросы о проводимости исследуемого материала (в настоящей работе этот материал - полупроводник p -типа).
В полупроводнике ток может быть разделен на электронную и дырочную составляющие:
 .
.
Здесь  - элементарный заряд,
- элементарный заряд,  и
и 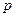 - концентрации электронов и дырок,
- концентрации электронов и дырок,  и
и  - средние скорости движения электронов и дырок.
- средние скорости движения электронов и дырок.
Движение носителей (дрейф) вызывается "продольным" полем  . Скорость дрейфа пропорциональна напряженности поля:
. Скорость дрейфа пропорциональна напряженности поля:

 .
.
Коэффициент пропорциональности m называется подвижностью носителей.
По закону Ома
 ,
,
и проводимость
 .
.
В примесном полупроводнике одна из составляющих преобладает, поэтому в полупроводнике n- и p- типа проводимость равна
 или
или  .
.
Различие в концентрациях носителей часто достигает нескольких порядков, тогда как отношение подвижностей не слишком велико (обычно  ), так что эти равенства выполняются с большой точностью.
), так что эти равенства выполняются с большой точностью.
Для определения проводимости материала может быть использован показанный на рис.1,б образец. Плотность тока через образец
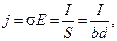
продольное напряжение на образце

здесь S - площадь поперечного сечения, l, b и d – длина, ширина и толщина образца. Отсюда получаем для полупроводника р - типа
 ,
,
или  . (2)
. (2)
Для измерения поперечной холловской разности потенциалов (холловского напряжения)  служат контакты а, a'. Если прибор для ее измерения имеет высокое входное сопротивление, то ток через контакты а, а' практически равен нулю. Поэтому справедливо выражение (1) и
служат контакты а, a'. Если прибор для ее измерения имеет высокое входное сопротивление, то ток через контакты а, а' практически равен нулю. Поэтому справедливо выражение (1) и
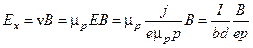 .
.
Холловское напряжение равно
 (3)
(3)
где величина
 (4)
(4)
называется постоянной Холла. Она зависит от концентрации носителей (в данном случае дырок), и поэтому, измеряя постоянную Холла, можно определить концентрацию носителей в полупроводнике.
Экспериментальная часть
Для проведения эксперимента используется электромагнит, между полюсами которого помещен полупроводниковый образец p - типа. Измерения производятся на стенде (рис.2), с помощью которого можно изменять и измерять величину и направление тока через образец, а также величину и направление тока электромагнита, создающего поперечное магнитное поле в образце. Продольное напряжение U на образце и поперечное холловское напряжение U х определяются по вольтметрам на стенде.

Рис 2. Передняя панель установки
Выполнение работы
1. Определение проводимости полупроводника
Измерения продольного напряжения U проведите при нескольких значениях тока в пределах от 0 до ~ 3 мА. При каждом значении тока определите U + и U - для обоих направлений тока. Изменение направления тока в образце производится вращением ручки ²регулирование тока в образце² по часовой стрелке и против часовой стрелки. В качестве результата примите среднее значение  модулей напряжений.
модулей напряжений.
Постройте график зависимости I (U). По графику этой зависимости найдите угловой коэффициент g и с помощью (2) рассчитайте проводимость s полупроводника.
Размеры образца: b = d = (5 ± 0,1) мм, l = (17 ± 0,1) мм.
2. Определение постоянной Холла, концентрации и подвижности носителей
При фиксированном токе через образец величиной I ~ 2,5 мА снимите зависимость U x(B) величины холловского напряжения от индукции магнитного поля, изменяя величину I м тока через электромагнит.
Значение индукции В магнитного поля, создаваемого электромагнитом,определяется по формуле
В = 0,41× I м,
где величина тока I м через электромагнит подставляется в амперах (А), а величина индукции поля получается в теслах (Тл).
В реальном образце даже при отсутствии внешнего магнитного поля поперечная разность потенциалов обычно отлична от нуля. Это связано с не совсем симметричным расположением контактов а и а¢ (см. рис.1,б), служащих для измерения холловского напряжения. Для исключения этой ²паразитной² разности потенциалов следует измерить напряжения Ux + и Ux - при двух разных направлениях одного и того же тока I м через электромагнит и в качестве холловского напряжения взять
 .
.
Изменение направления тока в электромагните производится вращением ручки ²регулирование тока в электромагните² по часовой стрелке и против часовой стрелки.
По угловому коэффициенту графика зависимости U x(B) с помощью (3) найдите постоянную Холла R.
Используя (4), определите концентрацию р дырок в полупроводнике.
Используя найденную в пункте 1 проводимость s, найдите подвижность дырок mр в полупроводнике.
Литература
1. Савельев И.В. Курс общей физики. - М.: Астрель, АСТ. 2003 – кн.2, § 11.3
2. Сивухин Д. В. Общий курс физики. Электричество. - М.: ФИЗМАТЛИТ, 2002. - §§ 98, 100
Лабораторная работа № 5