Человек незнакомый с флексагонами будет удивлен, увидев следующиеназвания:дотриаконтагектагексафлексагон,дотриаконтаг-ектатетрафлексагон. Разобраться в этих названиях на самом деле не сложно. Каждое название состоит из трех частей: двух приставок и слова «флексагон».Первая приставка показывает порядок флексагона (число чередующихся поверхностей), вторая определяет форму флексагона.Приставки образуются из корней греческих и латинских числительных, применяемых для обозначений соединений по правилам номенклатуры органических соединений.
Примеры таких приставок приведены ниже.
| Число | Приставка | Число | Приставка |
| Ди- | Пентакоса- | ||
| Три- | Гексакоса- | ||
| Тетра- | Гептакоса- | ||
| Пента- | Октакоса- | ||
| Гекса- | Нонакоса- | ||
| Гепта- | Триаконта- | ||
| Окта- | Гентриаконта- | ||
| Нона- | Тетраконта- | ||
| Дека- | Гентетраконта- | ||
| Ундека- | Пентаконта- | ||
| Додека- | Гексаконта- | ||
| Тридека- | Гептаконта- | ||
| Терадека- | Октаконта- | ||
| Пентадека- | Эннеаконта- | ||
| Гексадека- | Гекта- | ||
| Гептадека- | Дотриаконтагекта- | ||
| Октадека- | |||
| Нонадека- | |||
| Эйкоси- | |||
| Генэйкоса- | |||
| Докоса- | |||
| Трикоса- | |||
| Тетракоса- |
Конструирование флексагонов
Конструирование гексафлексагона

Конструирование гексафлексагона можно осуществить в 3 этапа:
1 этап:
Подготовить изображенную ниже полоску бумаги. Прогнуть каждую линию, разделяющую полоску на треугольники, в обе стороны, чтобы будущий флексагон легко разворачивался. По линии ab правую часть согнуть назад (рис. б)
2 этап:
По линии cd верхнюю часть согнуть назад и положить на крайний левый треугольник (рис. в)
3 этап:
Левую часть согнуть назад и наклеить на треугольник с обратной стороны (рис. г)
Существуют также гептагексафлексагоны, которые собираются из зигзагообразных полосок бумаги. Заштрихованные линии на рисунке — это места склеивания.

Применение флексагонов
Флексагоны не так уж и распространены в современной науке и технике. Но нашли они своё применение в некоторых художественных отраслях.
Игрушки:


Открытки:

Головоломки:



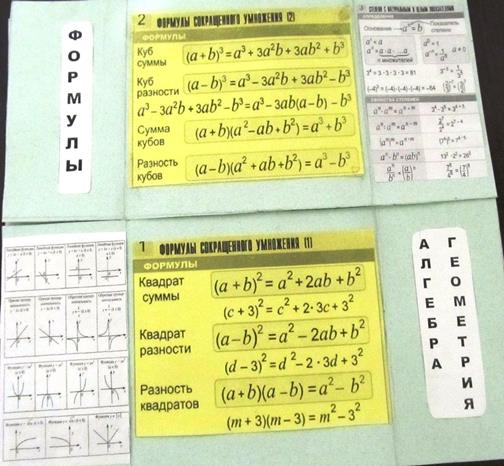
Справочные материалы:
Билборды:

Заключение
Флексагон – это математическая головоломка. Очень увлекательная, забавная игрушка, обладающая удивительными свойствами.Флексагоны не так уж и распространены в современной науке и технике. Но даже такие объекты как флексагоны, причем всех разновидностей нашли свое применение в некоторых художественных областях. Флексагоны выступают в роли игрушек и головоломок. Действительно, бывает иногда занимательно складывать флексагоны, выворачивать их, наблюдать, как они меняют форму и поворачиваются к нам разными комбинациями сторон. Используются как открытки на различные темы.
Выполнив свою работу, я познакомился с флексагонами, узнал их виды и применение. Научился делать их и давать им название.
Работа над флексагонами и флексорами расширила мои знания в математике. Я познакомился с ранее незнакомым мне видом флексагонов, увидел математику с совершенно другой неизвестной, но занимательной стороны. Я также понял, что эта другая сторона математики взаимосвязана с той чистой, обыденной математикой. Например, при изготовлении гексафлексагона, или кольца тетраэдров нужно чертить правильные треугольники и т. д.
Сам наглядно увидел, как работают флексагоны и флексоры. Гексафлексагоны действительно могут, выворачиваясь. изменять цвета. Увидел, что кольцо тетраэдров с 6 звеньями – жесткое, с 10 звеньями принимает симметричную форму, в виде звезды. С нечетным количеством звеньев кольцо принимает асимметричную форму, при 22 звеньях и больше кольца могут заузливаться.
Литература
1. И. Кан. Аномальные флексагоны. Ж. «Квант». – М.: «Наука», 1992. Вып. 10. С. 57 – 59.
2. И. Кан. Гемитетрафлексагоны. Ж. «Наука и жизнь». – М.: «Пресса», 1992. №4, С. 126 – 127
3. И. Кан. Гемитетра- и гемигексафлексагоны. Ж. «Наука и жизнь». – М.: «Пресса», 1993. №11, С. 150 – 152
4. И. Кан. Треугольные флексагоны. Ж. «Наука и жизнь». – М.: «Пресса», 1993. №12, С. 42 – 43
5. И. Константинов. Флексагонными тропами. Ж. «Наука и жизнь». – М.: «Правда», 1977. № 9, С. 92 – 96
6. https://www.popmech.ru/science/9331-shutka-geniev-fleksagon/
7. https://school-science.ru/2/7/30072
8. Гарднер М. Математические головоломки и развлечения: 2-е изд., испр. И дополн. / Пер. с англ. – М.: «Мир», 1999.
9. https://www.flexagon.net/
10. https://dic.academic.ru/dic.nsf/ruwiki/47435