Операторный метод расчета переходных процессов

Операторный метод расчета переходных процессов в электрических цепях

омск

УДК 621.30

ББК 31.211

 

Операторный метод расчета переходных процессов в электрических цепях: Методические указания для студентов / Российский заочный институт текстильной и легкой промышленности (филиал в г. Омске); Составил Н.Ф. Подковко. – Омск: 2007. – 10 с.

Предназначено для студентов специальности 220301.

 

Утверждено заседанием

Методического Совета филиала РосЗИТЛП в г. Омске.

Протокол №____ от «____» _____________ 20___ г.

 

 

© Подковко Н.Ф., 2007

© Российский заочный институт

текстильной и легкой

промышленности, 2007

- 3 -

Операторный метод расчета переходных процессов

Операторный метод относится к методам расчета пере­ходных процессов по комплексным значениям. В основу операторного метода расчета переходных процессов положено интегральное преобразование Лапласа:

,

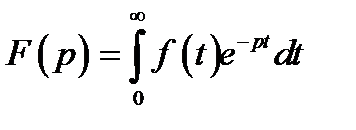где 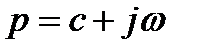– комплексная переменная, обычно называемая оператором, 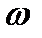– угловая частота, – некоторая вещественная постоянная. Примени­тельно к электрическим цепям оператор 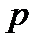можно рассматривать как комп­лексную частоту 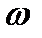, в которой 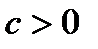характеризует затухание гармонических колебаний, представленных вращающимся вектором .

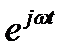Кроме интегрального преобразования Лапласа, в операторном методе расче­та часто используют интегральное преобразование Карсона-Хевисайда, кото­рое отличается от преобразования Лапласа дополнительным сомножителем :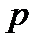

.

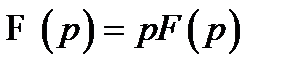Основным достоинством преобразования Карсона-Хевисайда является совпа­дение размерностей оригинала и изображения. Однако для практического ис­пользования операторного метода это особенность не имеет принципиального значения, поэтому в настоящем пособии используется преобразование Лапласа.

Преобразование подобного рода, но при условии 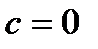и и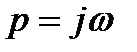с­пользуется при расчете цепей синусоидального

 

- 4 -

и несинусоидального периодического тока по комплексным значениям.

Особенностью применения интегрального преобразования Лапласа является возможность замены интегро-дифференциальных уравнений цепи, составлен­ных для функций времени 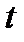алгебраическими уравнениями для функций опе­ратора 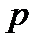. В результате этого система интегро-дифференциальных уравнений для мгновенных значений напряжений и токов заменяется системой алгебраичес­ких уравнений в операторной форме.

Алгоритм расчета цепей операторным методом состоит из трех основных этапов:

• составления операторной схемы замещения цепи;
• расчета операторной схемы замещения;
• определения оригинала реакции цепи по его операторному изображению.

Рассмотрим эти этапы расчета более подробно.

1. На этапе составления опера­торной схемы замещения необходимо выполнить следующие действия:

• рассчитать начальные условия в цепи для всех переменных состояния, т. е. для напряжений на емкостях и токов в индуктивностях до комму­тации цепи (при );
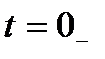• представить исходную схему после коммутации и, используя таблицу операторных соответствий (табл. 1), произвести замену элементов оригинальной схемы их операторными эквивалентами.

- 5 -

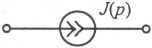
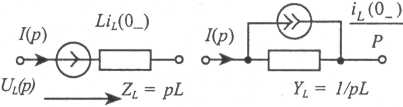
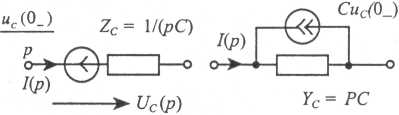
Таблица 1. Операторные схемы замещения элементов цепи

Элемент цепи	Оригинальная схема	Операторная схема
Источник напряжения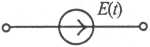
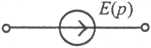
Источник тока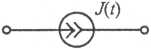
Сопротив-ление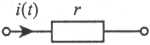
Индуктив- ность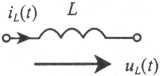
Емкость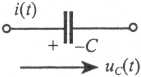

 

2. На этапе расчетаоператорной схемы замещения допускается использова­ние всех известных методов расчета цепей постоянного тока:

• законов Кирхгофа и любых эквивалентных преобразований,
• методов контурных токов и узловых напряжений,
• методов наложения и эквивалентного генератора.

При этом возможно решение как прямых, так и обратных задач, поскольку операторная схема замещения позволяет рассчитать изображения напряжений и токов всех ветвей цепи. Источники напряжений и токов,

- 6 -

соответствующие не­нулевым начальным условиям в исходной цепи, допускают любые эквивалент­ные преобразования, используемые для независимых источников. Некоторые функции и их операторные изображения приведены в табл. 2.

3. На этапе определения оригинала функции цепи по ее эквивалентному опера­торному изображению допускаются следующие способы:

• использование справочных таблиц операторного соответствия;
• применение формул разложения или вычетов.

Таблицы операторных соответствий приводятся в большинстве справочни­ков по математике. С помощью этих таблиц можно найти требуемую оператор­ную функцию 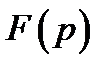и записать ее оригинал 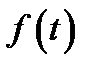. Некоторые из таких функций приведены в табл. 2.

Если операторное изображение 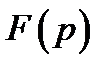представлено в виде дробно-рациональ­ной функции, у которой степень 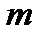полинома числителя 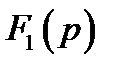не выше степени 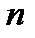полинома знаменателя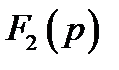

т. е. :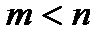

,

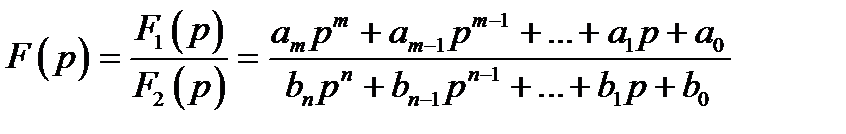то оригинал можно определить по формуле разложения, которая имеет вид

,

 

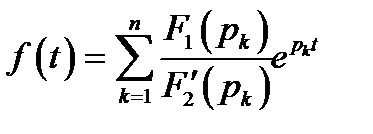- 7-

Таблица 2. Функции времени и их операторные изображения

№	Функция времени	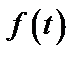Изображение по Лапласу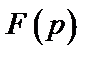

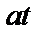
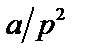
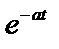
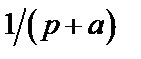
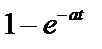
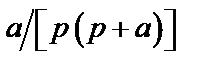
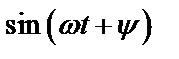
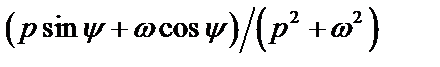
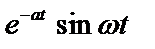
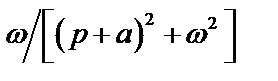
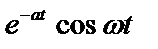
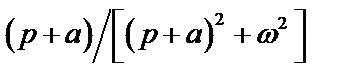
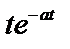
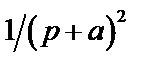
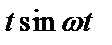
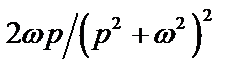
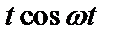
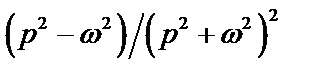
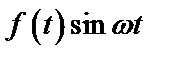
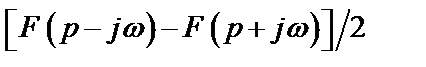
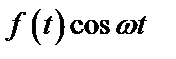
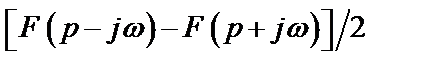
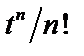
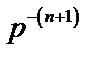
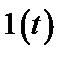
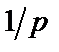
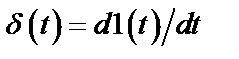
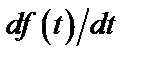
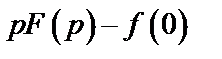
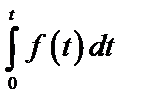
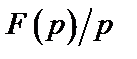
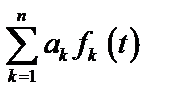
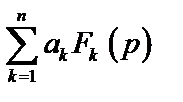
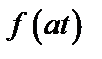
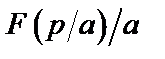
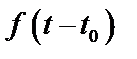
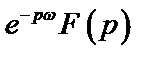
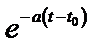
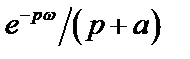
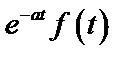
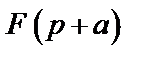
- 8 -

где 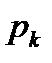– корни уравнения 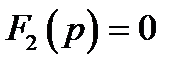, которые являются полюсами

функции 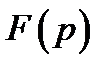; 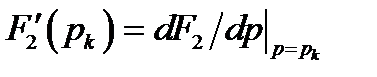– производная знаменателя при .

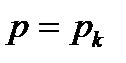Для определения оригинала можно также использовать формулу вычетов, которая имеет вид:

,

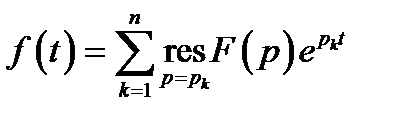где 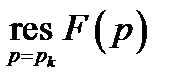– вычет функции 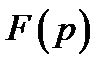в полюсе .

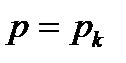Определение вычетов для случая дробно-рациональных дробей производит­ся по формуле

,

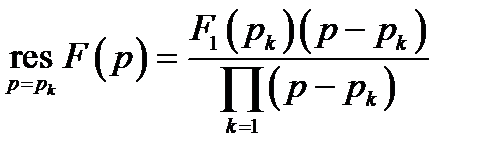откуда следует, что для определения вычета в полюсе 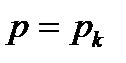необходимо значе­ние полюса подставить в числитель рациональной дроби 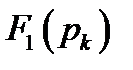, а в знаменате­ле, представленном в виде произведения 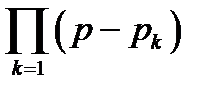, исключить член 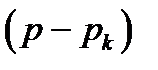при подстановке 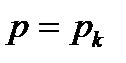(при этом многочлен знаменателя должен быть приве­денным, т. е. не содержать коэффициента при старшей степени ).

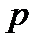Пример. Требуется рассчитать операторным методом переходный процесс в цепи второго порядка, схема которой изображена на рис. 1. Параметры элементов цепи имеют следующие значе­ния: Е = 40 В; r = 40 Ом; L = 1 Гн; С = 1/300 Ф.

 

 

- 9 -

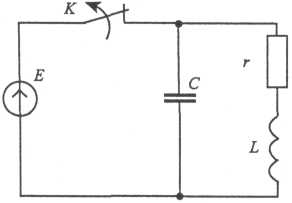
Рис. 1. Исходная схема цепи к примеру

Решение. Решение задачи начнем с построения операторной схемы замещения, которая должна соответствовать оригинальной схеме после размыкания ключа К. Эта схема приведена на рис. 2 и отличается от оригинальной тем, что в ней индуктивность, в соответствии с табл. 1, заменена сопротивлением 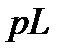и источником напряжения 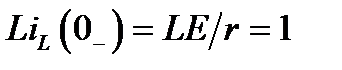В, а емкость – сопротивлением 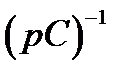и источником напряжения 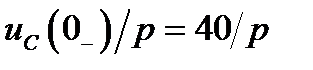В.

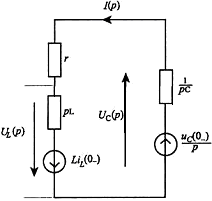
Рис. 2. Операторная схема замещения к примеру

- 10 -

Для расчета этой схемы составим уравнение по второму закону Кирхгофа:

,

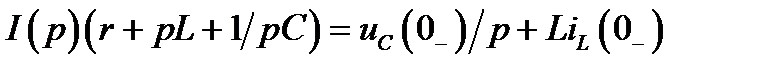из которого находим операторный ток

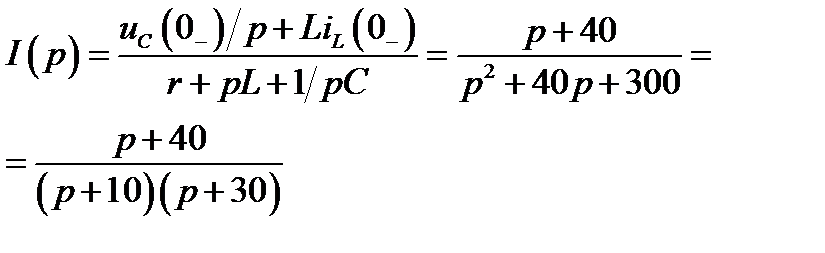
и операторные напряжения на емкости и индуктивности:

,

.

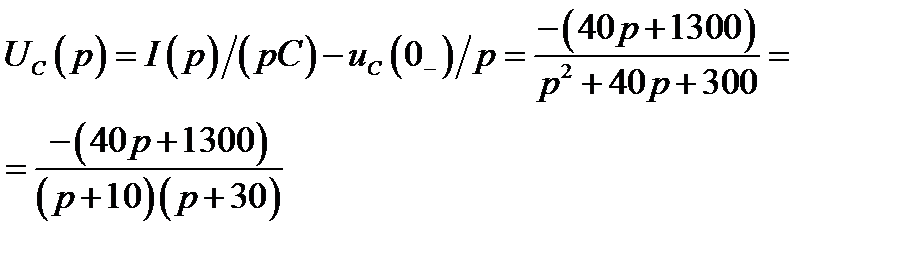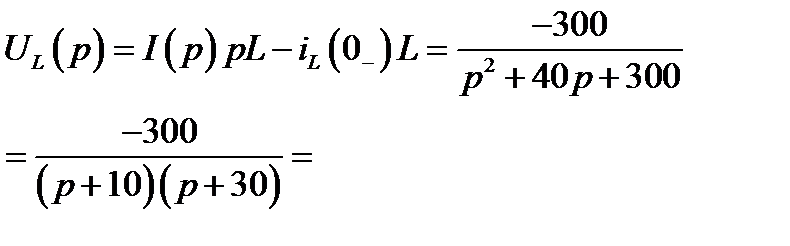Из полученных выражений следует, что корни знаменателя для тока и напряжений одинаковы и равны ; .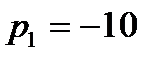

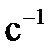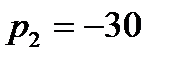
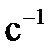Теперь, располагая операторными значениями тока и напряжений, определим их оригинальные (мгновенные) значения. Наиболее просто оригинальные значения можно определить по формуле вычетов. Для этого в знаменателе при подстановке значений корней следует исключить сомножители, которые обращаются в нуль. В числители всех вы­ражений значения корней подставляются непосредственно. Таким образом, после подстановки значений корней получим:

- 11 -

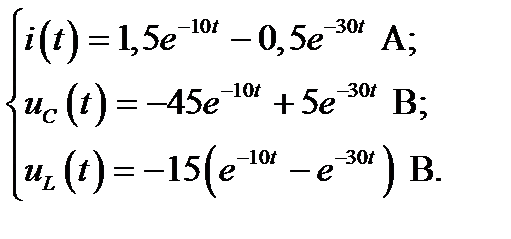
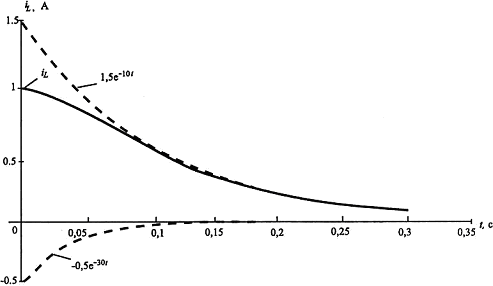
Графики тока и напряжений приведены на рис. 3.

а)

б) в)

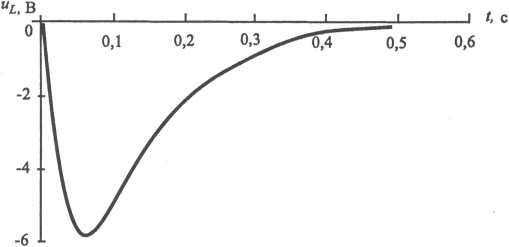
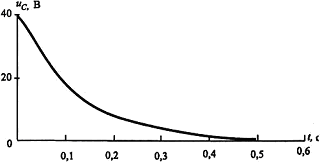
Рис. 3. Графики:

а) – тока 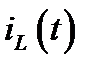; б) – напряжения 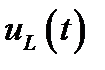; в) – напряжения