Лекция 6
Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Хk: 
Тема 5, зад.1
Пример 1. Случайная величина имеет закон распределения:
 . Найти начальные моменты 1-го, 2-го и 3-го порядков.
. Найти начальные моменты 1-го, 2-го и 3-го порядков.
Решение:  ;
;
 ;
;
 .
.
Центральным моментом порядка k случайной величины Х называется математическое ожидание величины  :
:

Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии.
Тема 5, зад.2
Пример 2. Случайная величина имеет закон распределения:

Найти центральные моменты 1-го, 2-го, 3-го и 4-го порядков.
Решение: 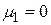 . Мат. ожидание посчитано выше
. Мат. ожидание посчитано выше  .
.
 .
.
 .
.
 .
.
Элементы математической статистики
Выборкой в математической статистике называется множество независимых одинаково распределенных случайных величин. Число реализаций в выборке (число повторных испытаний) N называется объемом выборки. Выборка подобна генеральной совокупности, из которой она извлечена.
Генеральной совокупностью называется множество всех возможных (мыслимых) значений случайной величины.
Рассмотрим выборку Х= x 1, x 2 ,... xn. Разобьем весь диапазон возможных значений случайной величины на d одинаковых участков. Ориентировочно, количество этих участков может быть определено по приближенной формуле:
 (формула не является обязательной).
(формула не является обязательной).
Значение на правой границе каждого участка находим как:
 ,
,
где i – номер участка; x max, x min – соответственно максимальное и минимальное значение случайной величины в выборке. Правая граница і -го участка вместе с тем есть левой границей (i +1)-го участка. Левая граница для 1-го участка – это x min. А правая граница последнего участка – это x max.
Количество значений случайной величины, которые попали в тот или другой участок обозначим Кі. Это число называется «частотой». «Относительной частотой» называется число  . Соответствие между значениями частоты (относительной частоты) и диапазоном значений случайной величины называется «гистограммой».
. Соответствие между значениями частоты (относительной частоты) и диапазоном значений случайной величины называется «гистограммой».
Оценки числовых характеристик случайной величины
Оценкой будем называть найденное по выборке число, которое в последующем используется вместо оцениваемого параметра. Настоящие моменты можно определить только проведя вычисление тысяч и тысяч значений случайной величины. Оценочные характеристики будем записывать с тремя чёрточками, чтобы подчеркнуть, что это не их точное значение, а только оценка.
– Оценка математического ожидания – это начальный момент первого порядка:  .
.
– Оценка дисперсии – центральный момент второго порядка, но с поправкой  :
:
 .
.
– Оценка среднего квадратичного отклонения:  .
.
Мерой относительного отклонения значений случайной величины относительно оценки среднего значения служит вариация 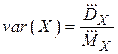 и коэффициент вариации
и коэффициент вариации  .
.
Мерой взаимной связи двух разных случайных величин служит корреляционный момент (этот параметр называется ещё ковариация), которая рассчитывается по выборкам:
 ,
,
где X, Y – соответственно первая и вторая случайные величины, а  ,
,  – их математические ожидания.
– их математические ожидания.
Чем большая корреляционный момент – тем большая связь этих случайных величин между собою.
Для приведения разных корреляционных моментов к одному масштабу, находится коэффициент корреляции (или просто корреляция):
 ,
,
где  – оценки средних квадратичных отклонений для случайных величин X и Y. Благодаря такому преобразованию коэффициент корреляции изменяется в диапазоне [–1,1]. Когда он равняется нулю, это означает, что связи между этими случайными величинами нет, а когда равняется 1 (или –1), это означает что эти случайные величины связаны между собою линейным соотношением вида Y = A×X + B. Здесь А и В – константы соотношения.
– оценки средних квадратичных отклонений для случайных величин X и Y. Благодаря такому преобразованию коэффициент корреляции изменяется в диапазоне [–1,1]. Когда он равняется нулю, это означает, что связи между этими случайными величинами нет, а когда равняется 1 (или –1), это означает что эти случайные величины связаны между собою линейным соотношением вида Y = A×X + B. Здесь А и В – константы соотношения.
Доверительный интервал
Представление о том, как далеко от оценок мат. ожидания, дисперсии и ср. кв. отклонения может находиться оцениваемый параметр, дают интервальные доверительные оценки.
Доверительным называется такой интервал, который в последующих испытаниях будет включать в себя (накрывать) оцениваемый параметр с заданной доверительной вероятностью –  . Уровень значимости, используемый в электронных таблицах Microsoft Excel будет найден как
. Уровень значимости, используемый в электронных таблицах Microsoft Excel будет найден как  .
.
Доверительный интервал для математического ожидания имеет вид:
 или
или  ,
,
где  – половина доверительного интервала.
– половина доверительного интервала.
Величина доверительного интервала равняется  . Такой интервал называется нормальным доверительным интервалом.
. Такой интервал называется нормальным доверительным интервалом.

Значение  для половины доверительного интервала находим:
для половины доверительного интервала находим:
– для математического ожидания:  ;
;
– для дисперсии:  ,
,
где z – обратное значение функции Лапласа, то есть такое значение аргумента (квантиля), при котором функция Лапласа (прил. 2) равняется  .
.
Пример 3. В результате семи независимых измерений некоторой физической величины, выполненных с одинаковой точностью, получены опытные данные: 15, 2, 17, 21, 7, 13, 29. Построить гистограмму и оценить математическое ожидание с доверительной вероятностью  . Найти доверительный интервал для математического ожидания и для дисперсии.
. Найти доверительный интервал для математического ожидания и для дисперсии.
Решение: x min=2, x max=29. Количество участков разбивки:

Принимаем  . Находим значение случайной величины на правой границе каждого из четырёх участков по формуле:
. Находим значение случайной величины на правой границе каждого из четырёх участков по формуле:  .
.
 ,
,  ,
,
 ,
,  .
.
Находим Кі,  .
.
Сводим все значения в таблицу и строим гистограмму.
| № | Границы участка | Частота, K i | Относительная частота, k i |
| 2 £ x < 9 | 0,286 | ||
| 9 £ x < 16 | 0,286 | ||
| 16 £ x < 22 | 0,286 | ||
| 22 £ x £ 29 | 0,142 |

Оценка математического ожидания:

Оценка дисперсии:

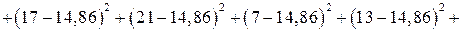


Оценка среднего квадратичного отклонения  .
.
Доверительный интервал для математического ожидания имеет вид:

Для  по таблице прил. 2 интегральной функции стандартного нормального распределения находим значение квантиля функции Лапласа
по таблице прил. 2 интегральной функции стандартного нормального распределения находим значение квантиля функции Лапласа 
Значение  для математического ожидания находим как:
для математического ожидания находим как:
 .
.
Доверительный интервал для мат. ожидания будет:  .
.
Значение  для дисперсии находим как:
для дисперсии находим как:
 .
.
Доверительный интервал для дисперсии будет:  .
.