Векторная алгебра
Обозначения:  { ax, ay,az },
{ ax, ay,az },  { ax, ay,az };
{ ax, ay,az };  ,
,  - модуль вектора (длина отрезка AB); ax, ay,az координаты вектора
- модуль вектора (длина отрезка AB); ax, ay,az координаты вектора  (проекции вектора
(проекции вектора  на оси координат). Точки А(xA,yA,zA), B(xB,yB,zB)
на оси координат). Точки А(xA,yA,zA), B(xB,yB,zB)
Выражение координат вектора через координаты его начала и конца
 { xB-xA,yB –yA,zB –zA } { xB-xA,yB –yA,zB –zA }
| Условие коллинеарности векторов
 =k
k>0 =k
k>0   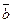 ; k<0 ; k<0   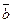
|
Основное свойство направляющих косинусов:

|  = = 
|
Обозначим a,β,  - углы, которые вектор составляет с осями координат OX, OY и OZ соответственно, cos a, cos β и cos
- углы, которые вектор составляет с осями координат OX, OY и OZ соответственно, cos a, cos β и cos  называются направляющими косинусами вектора.
называются направляющими косинусами вектора.
cos a=  ; cos β =
; cos β =  ; cos
; cos  =
=  ;
;
Линейные операции
1.  =
= 
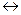

 2.
2.  {0,0,0} 3.
{0,0,0} 3.  ±
±  ={ ax± bx, ay± by, az ±bz }
={ ax± bx, ay± by, az ±bz }
4.  =k
=k 
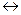
 (kax,kay,kaz)
(kax,kay,kaz)
Скалярное произведение векторов (
 )
)
Определение:   = =  , где , где  - угол между - угол между  и и  Замечание:
Замечание:  × ×  = =  × × 
| Вычисление:
  = = 
| Условие перпендикулярности векторов:  × ×  = 0 = 0 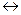  ^ ^ 
|

|
Векторное произведение ( )
)
Определение Векторным произведением вектора  на вектор
на вектор 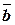 называется вектор
называется вектор  , определяемый следующими тремя условиями:
, определяемый следующими тремя условиями:
1)  , где
, где  - угол между векторами
- угол между векторами  и
и 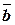 .
.
Отсюда следует, что модуль векторного произведения численно равен площади параллелограмма, построенного на векторах  и
и 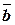 как на сторонах.
как на сторонах.
2) Вектор  перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов  и
и 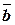 (
( ;
;  ), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах
), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах  и
и 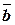 .
.
3) Вектор  направлен так, что если смотреть из его конца, то кратчайший поворот от вектора
направлен так, что если смотреть из его конца, то кратчайший поворот от вектора  к вектору
к вектору 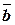 был бы против часовой стрелки (векторы
был бы против часовой стрелки (векторы  ,
, 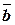 ,
,  образуют правую тройку).
образуют правую тройку).
Вычисление:

| Cвойства
1) 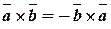 2) 2) 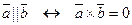 . .
| Площадь параллелограмма, построенного на векторах
 и и 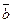 как на сторонах
S= как на сторонах
S= 
|
Смешанное произведение векторов (  )
)
Определение
 Замечание:
Замечание: 
| Вычисление:
 = = 
| Объем параллелепипеда, построенного на векторах
 , , 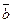 и и  как на сторонах
V= как на сторонах
V= 
|
Условие компланарности векторов:  , , 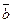 и и  компланарны компланарны 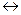 
|
Cвойства смешанного произведения
1) если в смешанном произведении перемножаемые векторы переставить в круговом порядке, то произведение не изменится:
 .
.
2)если в смешанном произведении поменять местами знаки векторного и скалярного умножения, то произведение не изменится:
 .
.
Это свойство позволяет записывать смешанное произведение в виде  без знаков векторного и скалярного умножения.
без знаков векторного и скалярного умножения.
3)перестановка в смешанном произведении любых двух векторов изменит лишь его знак:
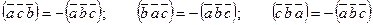
Свойства скалярного произведения:
1)  ×
×  = ï
= ï  ï2;
ï2;
2)  ×
×  = 0, если
= 0, если  ^
^  или
или  = 0 или
= 0 или  = 0.
= 0.
3)  ×
×  =
=  ×
×  ;
;
4)  ×(
×( +
+  ) =
) =  ×
×  +
+  ×
×  ;
;
5) (m  )×
)×  =
=  ×(m
×(m  ) = m(
) = m( ×
×  ); m=const
); m=const
Определение
Вычисление:

|
Свойства векторного произведения векторов.
1) Векторное произведение коллинеарных векторов равно нулю.
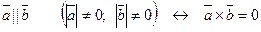 .
2) Антикоммутативность: .
2) Антикоммутативность: 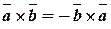 .
3) Ассоциативность относительно скалярного множителя:
( .
3) Ассоциативность относительно скалярного множителя:
( ).
4) Дистрибутивность: ).
4) Дистрибутивность:  . .
|
Векторное произведение двух векторов, заданных своими проекциями.
Пусть даны векторы  и
и  , тогда
, тогда
 .
.
Если рассматривать векторы 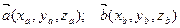 в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то

 ×
×  = xa xb + ya yb + za zb;
= xa xb + ya yb + za zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:

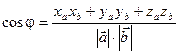 ;
;
Пример. Найти (5  + 3
+ 3  )(2
)(2  -
-  ), если
), если 
10  ×
×  - 5
- 5  ×
×  + 6
+ 6  ×
×  - 3
- 3  ×
×  = 10
= 10 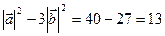 ,
,
т.к.  .
.
Пример. Найти угол между векторами  и
и  , если
, если 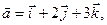
 .
.
Т.е.  = (1, 2, 3),
= (1, 2, 3),  = (6, 4, -2)
= (6, 4, -2)
 ×
×  = 6 + 8 – 6 = 8:
= 6 + 8 – 6 = 8:


1.  2.
2.  3.
3. 
| a) скалярное произведение векторов
 { ax, ay,az} и { ax, ay,az} и  {bx,by,bz}
б) векторное произведение векторов {bx,by,bz}
б) векторное произведение векторов
 { ax, ay,az} и { ax, ay,az} и  {bx,by,bz}
в) смешанное произведение векторов {bx,by,bz}
в) смешанное произведение векторов
 { ax, ay,az}, { ax, ay,az},  {bx,by,bz} и {bx,by,bz} и  {cx,cy,cz} {cx,cy,cz}
|
Укажите соответствие между вариантами взаимного расположения векторов и условиями, определяющими их выполнение
| Условия | Варианты расположения |
1.  2.
2. 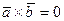 3.
3. 
| а) векторы коллинеарны б) векторы перпендикулярны в) векторы компланарны |
|