КУРСОВАЯ РАБОТА
по теории вероятностей и математической статистике
Исследование статистической зависимости двух случайных величин
Выполнила: студентка группы 2131
Коровина Яна Сергеевна Руководитель: Г.Э.Гришанина
Дубна, 2012
Введение
Математическая статистика — наука о математических методах систематизации и использовании статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (выборки).
Статистической зависимостью называется взаимосвязь двух признаков или величин, при которой распределение вероятностей одной из них зависит от того какие возможные значения приняла другая величина.
Для получения количественной характеристики вводится понятие случайной величины.
Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.
Случайные величины можно разделить на две категории.
1. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество. Это множество может быть как конечным, так и бесконечным.
2. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Задачи:
1. Построить диаграмму рассеивания.
2. Вычислить выборочные параметры: выборочные средние, выборочные и исправленные дисперсии, средние квадратические отклонения, моды и медианы выборки по X и по Y.
|
|
3. Вычислить корреляционный момент и коэффициент корреляции.
4. Построить корреляционную таблицу (8 на 8).
5. Построить полигоны, гистограммы нормированных относительных частот, эмпирические функции распределения по X и по Y.
6. Вычислить выборочные параметры: выборочные средние, выборочные и исправленные дисперсии, средние квадратические отклонения, моды и медианы выборки по X и по Y по корреляционной таблице.
7. Вычислить параметры для уравнения линейной регрессии Y на X, построить линию регрессии на диаграмме рассеивания.
8. Вычислить параметры для уравнения параболической регрессии, построить линию параболической регрессии на диаграмме рассеивания.
Исходные данные
| X | Y |
| 15,0 | 43,8 |
| 0,212 | 5,60 |
| 17,9 | 59,4 |
| 7,68 | 27,8 |
| 18,0 | 60,2 |
| 14,9 | 53,5 |
| 13,4 | 35,6 |
| 0,358 | 3,60 |
| 0,994 | 9,46 |
| 9,78 | 31,0 |
| 5,00 | 18,7 |
| 6,68 | 30,9 |
| 17,7 | 57,9 |
| 1,99 | 15,9 |
| 19,7 | 65,4 |
| 7,16 | 23,1 |
| 10,8 | 32,8 |
| 0,652 | 3,62 |
| 9,72 | 36,3 |
| 12,6 | 40,4 |
| 4,78 | 22,6 |
| 1,36 | -1,42 |
| 4,94 | 15,7 |
| 12,3 | 38,8 |
| 4,64 | 16,4 |
| 5,18 | 26,0 |
| 1,87 | 6,94 |
| 6,62 | 31,4 |
| 8,06 | 20,6 |
| 8,16 | 20,4 |
| 6,76 | 31,2 |
| 13,8 | 44,9 |
| 3,14 | 15,9 |
| 6,26 | 20,2 |
| 10,8 | 27,4 |
| 6,28 | 23,3 |
| 7,54 | 18,5 |
| 3,98 | 16,7 |
| 14,3 | 43,9 |
| 10,0 | 26,7 |
| 13,5 | 45,8 |
| 6,62 | 35,5 |
| 18,4 | 59,6 |
| 1,76 | 13,4 |
| 12,4 | 40,3 |
| 11,2 | 43,4 |
| 14,6 | 32,8 |
| 1,44 | 17,5 |
| 11,0 | 35,2 |
| 17,8 | 50,0 |
| 8,98 | 27,4 |
| 10,6 | 37,5 |
| 16,8 | 45,4 |
| 2,70 | 18,5 |
| 7,58 | 36,3 |
| 12,3 | 30,1 |
| 4,06 | 21,5 |
| 0,244 | 6,78 |
| 4,86 | 12,6 |
| 9,48 | 31,8 |
| 15,7 | 52,0 |
| 13,5 | 42,8 |
| 16,6 | 50,9 |
| 12,1 | 34,8 |
| 15,0 | 50,2 |
| 12,2 | 46,3 |
| 8,06 | 39,2 |
| 17,6 | 51,3 |
| 19,7 | 63,9 |
| 9,98 | 31,6 |
| 16,4 | 48,6 |
| 17,8 | 56,3 |
| 5,42 | 23,7 |
| 6,98 | 25,4 |
| 5,98 | 18,8 |
| 4,22 | 11,9 |
| 1,06 | 7,32 |
| 9,92 | 36,9 |
| 17,1 | 44,0 |
| 9,34 | 22,0 |
| 19,2 | 57,0 |
| 3,54 | 15,4 |
| 4,64 | 23,2 |
| 9,60 | 38,1 |
| 7,48 | 28,9 |
| 6,54 | 28,8 |
| 1,10 | 6,06 |
| 19,4 | 62,0 |
| 4,52 | 24,5 |
| 8,78 | 41,7 |
| 3,54 | 11,6 |
| 16,7 | 52,1 |
| 9,70 | 35,3 |
| 1,97 | 10,6 |
| 17,1 | 47,0 |
| 6,14 | 22,0 |
| 3,24 | 5,10 |
| 8,04 | 28,3 |
| 6,70 | 20,0 |
| 9,56 | 39,4 |
|
|
Диаграммы рассеивания
Диаграмма рассеяния — математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости.
На диаграмме рассеяния каждому наблюдению (или элементарной единице набора данных) соответствует точка, координаты которой (в декартовой системе координат) равны значениям двух каких-то параметров этого наблюдения.
Выборочные параметры
| По Х | По У | |
| Среднее | 9,1947 | 31,1746 |
| Медиана | 8,47 | 30,95 |
| Мода | 15,9 | |
| Квадратическое отклонение | 5,52280824025113 | 16,0405143258682 |
| Исправленная дисперсия | 16,0405143258682 | 16,0405143258682 |
| Выборочная дисперсия | 30,5014108585858 | 257,298099838384 |
| Ковариация | 82,91371138 | |
| Корреляция | 0,945394142636072 |
Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.
Мода – величина признака, которая чаще всего встречается в данной совокупности.
Медианой называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности.
Среднеквадратическое отклонение — это наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений, а исправленная дисперсия является несмещённой оценкой.
Ковариация (корреляционный момент) — это мера линейной зависимости двух случайных величин.
|
|
Корреляция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин.
Корреляционная таблица
Пусть величина Х в выборке принимает значения x1, x2,....xm, где количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке может повторяться. Пусть величина Y в выборке принимает значения y1, y2,....yk, где k - количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке также может повторяться. В этом случае данные заносят в таблицу с учетом частот встречаемости. Такую таблицу с группированными данными называют корреляционной.
| 0;2,5 | 2,5; 5 | 5; 7,5 | 7,5; 10 | 10;12,5 | 12,5;15 | 15;17,5 | 17,5; 20 | |
| -2; 6,5 | ||||||||
| 6,5;15 | ||||||||
| 15; 23,5 | ||||||||
| 23,5; 32 | ||||||||
| 32; 40,5 | ||||||||
| 40,5; 49 | ||||||||
| 49; 57,5 | ||||||||
| 57,5; 66 |
Вычисление выборочных параметров по корреляционной таблице
Выборочное среднее 
называют среднее арифметическое значение признака выборочной совокупности.
Среднее (арифметическое) 
определяется по формуле
,
где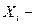 
варианты X, 
соответствующие частоты,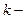 
количество вариантов, 
объём выборки.
= 1/100(1.75 *5 + 3.75*1) = 0.125
Выборочной дисперсией 
называют среднее квадратическое квадратов отклонении наблюдаемых значений признака от их среднего значения и определяется по формуле
D(x) = M(
) - 
D(x) = (1.75^2 *5+ 3.75^2*1) – 0,125^2 = 15.3125 + 14.0625 – 0.01562 = 29.39062
Исправленная дисперсия это несмещённая оценка генеральной дисперсии. Она определяется по формуле 
= 100/99*29.39062 = 29.68749
Среднее квадратическое отклонение вычисляется по формуле 
Мода – самое частое встречающиеся в выборке число.
Медиана - середина вариационного ряда.
1,1,1,1,2,2,2,2,3,3,3,4,4,4,5,5,6,6,6,7,7,7,8,10
Полигон
Полигон - о дин из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.
Гистограмма
Гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки.
