Правило сложения дисперсии в статистике

Прямолинейная

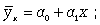
криволинейная в виде:

параболы второго порядка (или высших порядков)

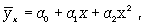
гиперболы

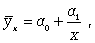(8.3)

показательной функции

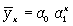
и т.д.

Параметры для всех этих уравнений связи, как правило, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК):

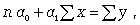
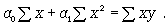
Если связь выражена параболой второго порядка (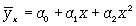), то систему нормальных уравнений для отыскания параметров a₀, a₁, a₂ (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представть в виде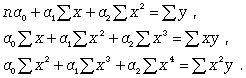

42.
- измерение тесноты зависимости - для всех форм связи может быть решена при помощи вычисления эмпирического корреляционного отношения :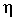

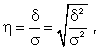(8.7)

где - дисперсия в ряду выравненных значений результативного показателя ; 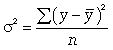- дисперсия в ряду фактических значений у.

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:

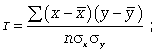(8.8)

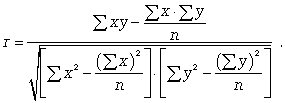
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.

43. Парная линейная корреляция

Парная, или однофакторная, корреляция — это неполная пря­мая или обратная связь между одним признаком-следствием и одним признаком-фактором. Она позволяет относительно аде­кватно измерить выявленную связь, чего не дают другие методы статистического анализа. Ценность корреляционного анализа сле­дует оценивать, исходя из известного постулата: наука начина­ется с измерения.

Корреляционное измерение связи, как правило, производится после установления ее наличия и характера (прямая, обратная) в процессе других видов статистического анализа: сводки и груп­пировки данных, расчета относительных и средних величин, со­ставления вариационных, динамических и особенно параллель­ных рядов.

17. Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:

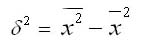
2. Взвешенная дисперсия (для вариационного ряда):

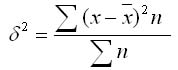
где n - частота (повторяемость фактора Х)

Правило сложения дисперсии в статистике

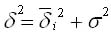Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.